
Question Number 218658 by Nicholas666 last updated on 14/Apr/25
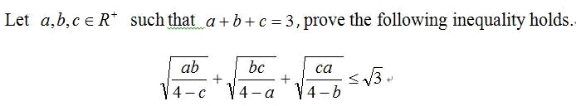
Answered by Nicholas666 last updated on 14/Apr/25
Commented by A5T last updated on 14/Apr/25
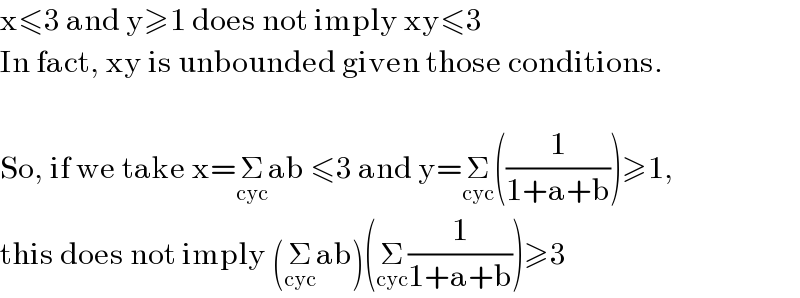
$$\mathrm{x}\leqslant\mathrm{3}\:\mathrm{and}\:\mathrm{y}\geqslant\mathrm{1}\:\mathrm{does}\:\mathrm{not}\:\mathrm{imply}\:\mathrm{xy}\leqslant\mathrm{3} \\ $$$$\mathrm{In}\:\mathrm{fact},\:\mathrm{xy}\:\mathrm{is}\:\mathrm{unbounded}\:\mathrm{given}\:\mathrm{those}\:\mathrm{conditions}. \\ $$$$ \\ $$$$\mathrm{So},\:\mathrm{if}\:\mathrm{we}\:\mathrm{take}\:\mathrm{x}=\underset{\mathrm{cyc}} {\sum}\mathrm{ab}\:\leqslant\mathrm{3}\:\mathrm{and}\:\mathrm{y}=\underset{\mathrm{cyc}} {\sum}\left(\frac{\mathrm{1}}{\mathrm{1}+\mathrm{a}+\mathrm{b}}\right)\geqslant\mathrm{1}, \\ $$$$\mathrm{this}\:\mathrm{does}\:\mathrm{not}\:\mathrm{imply}\:\left(\underset{\mathrm{cyc}} {\sum}\mathrm{ab}\right)\left(\underset{\mathrm{cyc}} {\sum}\frac{\mathrm{1}}{\mathrm{1}+\mathrm{a}+\mathrm{b}}\right)\geqslant\mathrm{3} \\ $$
Answered by A5T last updated on 14/Apr/25
![4−c=1+a+b; 4−b=1+a+c; 4−a=1+b+c 1+a+b≥3((ab))^(1/3) ⇒((ab)/(1+a+b))≤((ab)/(3((ab))^(1/3) ))=(1/3)(ab)^(2/3) ⇒Σ(√((ab)/(1+a+b)))≤((√3)/3)Σ(ab)^(1/3) But [((Σ(ab)^(1/3) )/3)]^3 ≤((Σ(ab))/3)=((ab+bc+ca)/3)≤(((a+b+c)^2 )/9)=1 ⇒Σ(ab)^(1/3) ≤3 ⇒Σ(√((ab)/(1+a+b)))≤((√3)/3)×3=(√3) Equality when a=b=c=1](Q218717.png)
$$\mathrm{4}−\mathrm{c}=\mathrm{1}+\mathrm{a}+\mathrm{b};\:\mathrm{4}−\mathrm{b}=\mathrm{1}+\mathrm{a}+\mathrm{c};\:\mathrm{4}−\mathrm{a}=\mathrm{1}+\mathrm{b}+\mathrm{c} \\ $$$$\mathrm{1}+\mathrm{a}+\mathrm{b}\geqslant\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{ab}}\Rightarrow\frac{\mathrm{ab}}{\mathrm{1}+\mathrm{a}+\mathrm{b}}\leqslant\frac{\mathrm{ab}}{\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{ab}}}=\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{ab}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} \\ $$$$\Rightarrow\Sigma\sqrt{\frac{\mathrm{ab}}{\mathrm{1}+\mathrm{a}+\mathrm{b}}}\leqslant\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\Sigma\left(\mathrm{ab}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$\mathrm{But}\:\left[\frac{\Sigma\left(\mathrm{ab}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} }{\mathrm{3}}\right]^{\mathrm{3}} \leqslant\frac{\Sigma\left(\mathrm{ab}\right)}{\mathrm{3}}=\frac{\mathrm{ab}+\mathrm{bc}+\mathrm{ca}}{\mathrm{3}}\leqslant\frac{\left(\mathrm{a}+\mathrm{b}+\mathrm{c}\right)^{\mathrm{2}} }{\mathrm{9}}=\mathrm{1} \\ $$$$\Rightarrow\Sigma\left(\mathrm{ab}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \leqslant\mathrm{3} \\ $$$$\Rightarrow\Sigma\sqrt{\frac{\mathrm{ab}}{\mathrm{1}+\mathrm{a}+\mathrm{b}}}\leqslant\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}×\mathrm{3}=\sqrt{\mathrm{3}} \\ $$$$\mathrm{Equality}\:\mathrm{when}\:\mathrm{a}=\mathrm{b}=\mathrm{c}=\mathrm{1} \\ $$
