Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 218651 by hardmath last updated on 13/Apr/25

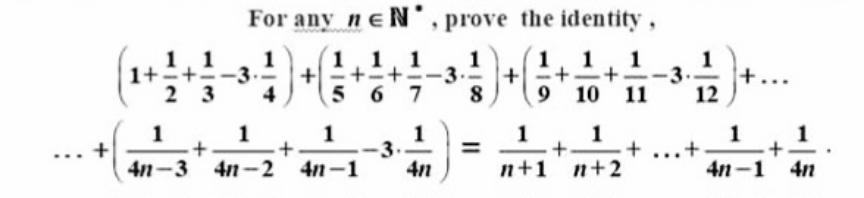
Answered by vnm last updated on 14/Apr/25

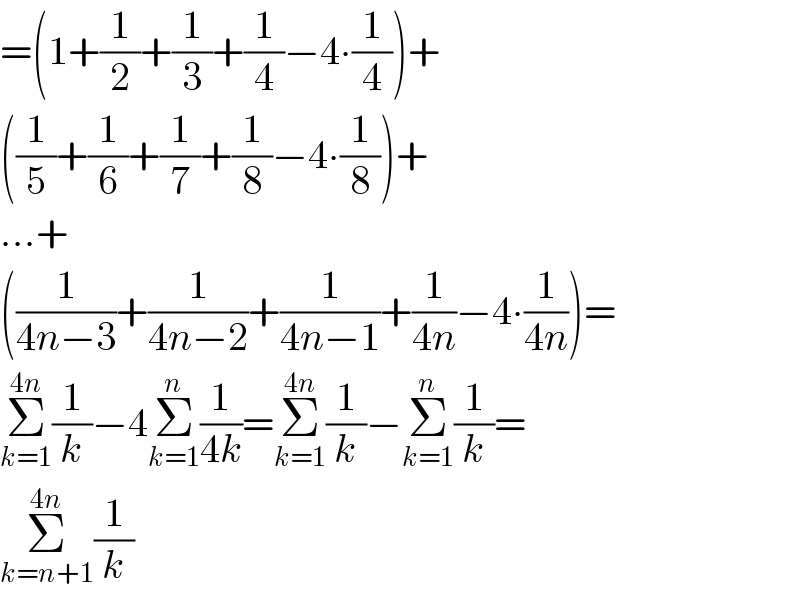
=(1+(1/2)+(1/3)+(1/4)−4∙(1/4))+ ((1/5)+(1/6)+(1/7)+(1/8)−4∙(1/8))+ ...+ ((1/(4n−3))+(1/(4n−2))+(1/(4n−1))+(1/(4n))−4∙(1/(4n)))= Σ_(k=1) ^(4n) (1/k)−4Σ_(k=1) ^n (1/(4k))=Σ_(k=1) ^(4n) (1/k)−Σ_(k=1) ^n (1/k)= Σ_(k=n+1) ^(4n) (1/k)

$$=\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{4}\centerdot\frac{\mathrm{1}}{\mathrm{4}}\right)+ \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{7}}+\frac{\mathrm{1}}{\mathrm{8}}−\mathrm{4}\centerdot\frac{\mathrm{1}}{\mathrm{8}}\right)+ \\ $$$$...+ \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{4}{n}−\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}{n}−\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}{n}−\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{4}{n}}−\mathrm{4}\centerdot\frac{\mathrm{1}}{\mathrm{4}{n}}\right)= \\ $$$$\underset{{k}=\mathrm{1}} {\overset{\mathrm{4}{n}} {\sum}}\frac{\mathrm{1}}{{k}}−\mathrm{4}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{4}{k}}=\underset{{k}=\mathrm{1}} {\overset{\mathrm{4}{n}} {\sum}}\frac{\mathrm{1}}{{k}}−\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{k}}= \\ $$$$\underset{{k}={n}+\mathrm{1}} {\overset{\mathrm{4}{n}} {\sum}}\frac{\mathrm{1}}{{k}} \\ $$

Commented by hardmath last updated on 17/Apr/25

thank you my dear professor

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{my}\:\mathrm{dear}\:\mathrm{professor} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com