
Question Number 218636 by hardmath last updated on 13/Apr/25
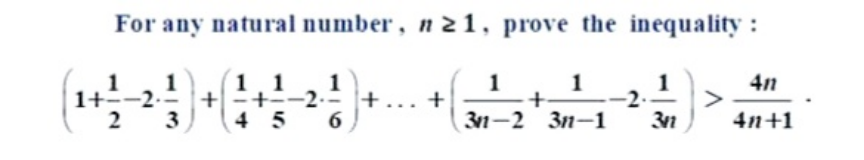
Answered by vnm last updated on 14/Apr/25
![let a_k =(1/(3k−1))+(1/(3k−2))−(2/(3k)) b_k =((4k)/(4k+1))−((4(k−1))/(4(k−1)+1)) if ∀k≥1 a_k >b_k then ∀n≥1 Σ_(k=1) ^n a_k >Σ_(k=1) ^n b_k =((4n)/(4n+1)) a_k =((9k−4)/(3(3k−2)(3k−1)k)) b_k =(4/((4k+1)(4k−3))) a_k −b_k =((9k−4)/(3(3k−2)(3k−1)k))−(4/((4k+1)(4k−3)))= ((36k^3 −28k^2 −19k+12)/(3k(3k−2)(3k−1)(4k+1)(4k−3))) 36k^3 −28k^2 −19k+12=[2k=m]= (1/2)(9m^3 −14m^2 −19m+24)= (1/2)(m−1)(9m^2 −5m−24)=0 m_1 =1, m_(2,3) =((5±(√(889)))/(18)) ((5+(√(889)))/(18))<((5+30)/(18))<2⇒∀k≥1 a_k −b_k >0](Q218653.png)
$${let} \\ $$$$\:{a}_{{k}} =\frac{\mathrm{1}}{\mathrm{3}{k}−\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{3}{k}−\mathrm{2}}−\frac{\mathrm{2}}{\mathrm{3}{k}} \\ $$$${b}_{{k}} =\frac{\mathrm{4}{k}}{\mathrm{4}{k}+\mathrm{1}}−\frac{\mathrm{4}\left({k}−\mathrm{1}\right)}{\mathrm{4}\left({k}−\mathrm{1}\right)+\mathrm{1}} \\ $$$${if}\:\:\forall{k}\geqslant\mathrm{1}\:{a}_{{k}} >{b}_{{k}} \:{then} \\ $$$$\forall{n}\geqslant\mathrm{1}\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{k}} >\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{b}_{{k}} =\frac{\mathrm{4}{n}}{\mathrm{4}{n}+\mathrm{1}} \\ $$$${a}_{{k}} =\frac{\mathrm{9}{k}−\mathrm{4}}{\mathrm{3}\left(\mathrm{3}{k}−\mathrm{2}\right)\left(\mathrm{3}{k}−\mathrm{1}\right){k}} \\ $$$${b}_{{k}} =\frac{\mathrm{4}}{\left(\mathrm{4}{k}+\mathrm{1}\right)\left(\mathrm{4}{k}−\mathrm{3}\right)} \\ $$$${a}_{{k}} −{b}_{{k}} =\frac{\mathrm{9}{k}−\mathrm{4}}{\mathrm{3}\left(\mathrm{3}{k}−\mathrm{2}\right)\left(\mathrm{3}{k}−\mathrm{1}\right){k}}−\frac{\mathrm{4}}{\left(\mathrm{4}{k}+\mathrm{1}\right)\left(\mathrm{4}{k}−\mathrm{3}\right)}= \\ $$$$\frac{\mathrm{36}{k}^{\mathrm{3}} −\mathrm{28}{k}^{\mathrm{2}} −\mathrm{19}{k}+\mathrm{12}}{\mathrm{3}{k}\left(\mathrm{3}{k}−\mathrm{2}\right)\left(\mathrm{3}{k}−\mathrm{1}\right)\left(\mathrm{4}{k}+\mathrm{1}\right)\left(\mathrm{4}{k}−\mathrm{3}\right)} \\ $$$$\mathrm{36}{k}^{\mathrm{3}} −\mathrm{28}{k}^{\mathrm{2}} −\mathrm{19}{k}+\mathrm{12}=\left[\mathrm{2}{k}={m}\right]= \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{9}{m}^{\mathrm{3}} −\mathrm{14}{m}^{\mathrm{2}} −\mathrm{19}{m}+\mathrm{24}\right)= \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left({m}−\mathrm{1}\right)\left(\mathrm{9}{m}^{\mathrm{2}} −\mathrm{5}{m}−\mathrm{24}\right)=\mathrm{0} \\ $$$${m}_{\mathrm{1}} =\mathrm{1},\:\:{m}_{\mathrm{2},\mathrm{3}} =\frac{\mathrm{5}\pm\sqrt{\mathrm{889}}}{\mathrm{18}} \\ $$$$\frac{\mathrm{5}+\sqrt{\mathrm{889}}}{\mathrm{18}}<\frac{\mathrm{5}+\mathrm{30}}{\mathrm{18}}<\mathrm{2}\Rightarrow\forall{k}\geqslant\mathrm{1}\:{a}_{{k}} −{b}_{{k}} >\mathrm{0} \\ $$
Commented by hardmath last updated on 17/Apr/25
$$\mathrm{thankyou}\:\mathrm{dearprofessor} \\ $$
