Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

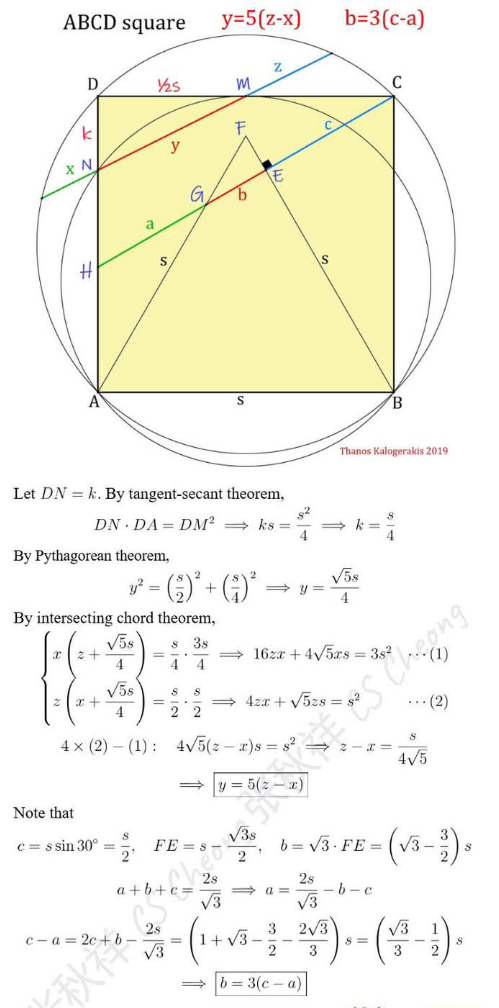
Question Number 218607 by Spillover last updated on 13/Apr/25

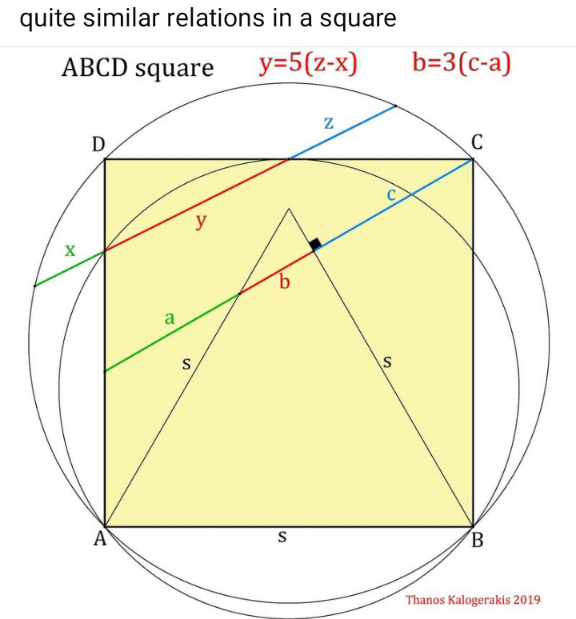
Answered by mr W last updated on 13/Apr/25

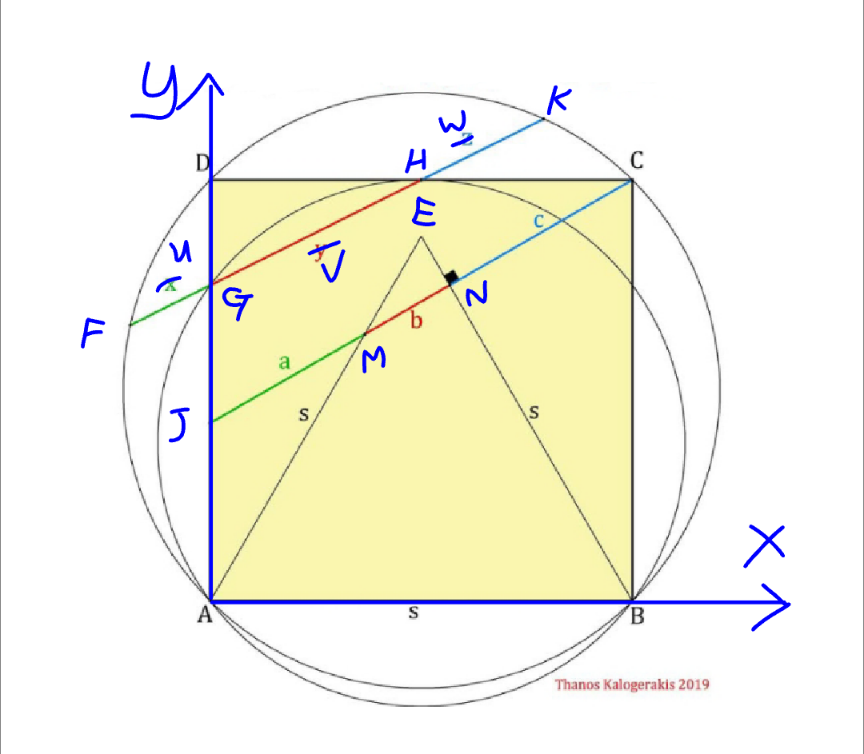
Commented by mr W last updated on 13/Apr/25

bigger circle: (x−(s/2))^2 +(y−(s/2))^2 =(s^2 /2) smaller circle: (x−(s/2))^2 +(y−((3s)/8))^2 =(((5s)/8))^2 (−(s/2))^2 +(y_G −((3s)/8))^2 =(((5s)/8))^2 ⇒y_G =((3s)/4) eqn. of GH: y=s+(1/2)(x−(s/2))=(x/2)+((3s)/4) (x−(s/2))^2 +((x/2)+((3s)/4)−(s/2))^2 =(s^2 /2) 5x^2 −3sx−((3s^2 )/4)=0 x=(((3±2(√6))/(10)))s ⇒x_F =(((3−2(√6))s)/(10)) ⇒x_K =(((3+2(√6))s)/(10)) Δx_(GF) =x_G −x_F =(((2(√6)−3)s)/(10)) Δx_(HK) =x_K −x_H =(((3+2(√6))s)/(10))−(s/2)=(((2(√6)−2)s)/(10)) ((w−u)/v)=((Δx_(HK) −Δx_(GF) )/(Δx_(EG) )) =(((((2(√6)−2)s)/(10))−(((2(√6)−3)s)/(10)))/(s/2))=(1/5) ⇒v=5(w−u) ≡ y=5(z−x) in original question✓ eqn. of JC: y=s+((x−s)/( (√3)))=(x/( (√3)))+(1−(1/( (√3))))s eqn. of AE: y=(√3)x y_M =(√3)x_M =(x_M /( (√3)))+(1−(1/( (√3))))s ⇒x_M =((((√3)−1)s)/2) eqn. of BE: y=−(√3)(x−s) y_N =−(√3)(x_N −s)=(x_N /( (√3)))+(1−(1/( (√3))))s ⇒x_N =(((4−(√3))s)/4) Δx_(MJ) =x_M −x_J =((((√3)−1)s)/2) Δx_(CN) =x_C −x_N =s−(((4−(√3))s)/4)=(((√3)s)/4) Δx_(NM) =x_N −x_M =(((4−(√3))s)/4)−((((√3)−1)s)/2)=((3(2−(√3))s)/4) ((c−a)/b)=((Δx_(CN) −Δx_(MJ) )/(Δx_(MN) )) =(((((√3)s)/4)−((((√3)−1)s)/2))/((3(2−(√3))s)/4))=(1/3) ⇒b=3(c−a) ✓

$${bigger}\:{circle}: \\ $$$$\left({x}−\frac{{s}}{\mathrm{2}}\right)^{\mathrm{2}} +\left({y}−\frac{{s}}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{{s}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${smaller}\:{circle}: \\ $$$$\left({x}−\frac{{s}}{\mathrm{2}}\right)^{\mathrm{2}} +\left({y}−\frac{\mathrm{3}{s}}{\mathrm{8}}\right)^{\mathrm{2}} =\left(\frac{\mathrm{5}{s}}{\mathrm{8}}\right)^{\mathrm{2}} \\ $$$$ \\ $$$$\left(−\frac{{s}}{\mathrm{2}}\right)^{\mathrm{2}} +\left({y}_{{G}} −\frac{\mathrm{3}{s}}{\mathrm{8}}\right)^{\mathrm{2}} =\left(\frac{\mathrm{5}{s}}{\mathrm{8}}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{y}_{{G}} =\frac{\mathrm{3}{s}}{\mathrm{4}} \\ $$$${eqn}.\:{of}\:{GH}: \\ $$$${y}={s}+\frac{\mathrm{1}}{\mathrm{2}}\left({x}−\frac{{s}}{\mathrm{2}}\right)=\frac{{x}}{\mathrm{2}}+\frac{\mathrm{3}{s}}{\mathrm{4}} \\ $$$$\left({x}−\frac{{s}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{{x}}{\mathrm{2}}+\frac{\mathrm{3}{s}}{\mathrm{4}}−\frac{{s}}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{{s}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\mathrm{5}{x}^{\mathrm{2}} −\mathrm{3}{sx}−\frac{\mathrm{3}{s}^{\mathrm{2}} }{\mathrm{4}}=\mathrm{0} \\ $$$${x}=\left(\frac{\mathrm{3}\pm\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{10}}\right){s} \\ $$$$\Rightarrow{x}_{{F}} =\frac{\left(\mathrm{3}−\mathrm{2}\sqrt{\mathrm{6}}\right){s}}{\mathrm{10}} \\ $$$$\Rightarrow{x}_{{K}} =\frac{\left(\mathrm{3}+\mathrm{2}\sqrt{\mathrm{6}}\right){s}}{\mathrm{10}} \\ $$$$\Delta{x}_{{GF}} ={x}_{{G}} −{x}_{{F}} =\frac{\left(\mathrm{2}\sqrt{\mathrm{6}}−\mathrm{3}\right){s}}{\mathrm{10}} \\ $$$$\Delta{x}_{{HK}} ={x}_{{K}} −{x}_{{H}} =\frac{\left(\mathrm{3}+\mathrm{2}\sqrt{\mathrm{6}}\right){s}}{\mathrm{10}}−\frac{{s}}{\mathrm{2}}=\frac{\left(\mathrm{2}\sqrt{\mathrm{6}}−\mathrm{2}\right){s}}{\mathrm{10}} \\ $$$$\frac{{w}−{u}}{{v}}=\frac{\Delta{x}_{{HK}} −\Delta{x}_{{GF}} }{\Delta{x}_{{EG}} } \\ $$$$\:\:\:=\frac{\frac{\left(\mathrm{2}\sqrt{\mathrm{6}}−\mathrm{2}\right){s}}{\mathrm{10}}−\frac{\left(\mathrm{2}\sqrt{\mathrm{6}}−\mathrm{3}\right){s}}{\mathrm{10}}}{\frac{{s}}{\mathrm{2}}}=\frac{\mathrm{1}}{\mathrm{5}} \\ $$$$\Rightarrow{v}=\mathrm{5}\left({w}−{u}\right)\:\equiv\:{y}=\mathrm{5}\left({z}−{x}\right)\:{in}\:{original}\:{question}\checkmark \\ $$$$ \\ $$$${eqn}.\:{of}\:{JC}: \\ $$$${y}={s}+\frac{{x}−{s}}{\:\sqrt{\mathrm{3}}}=\frac{{x}}{\:\sqrt{\mathrm{3}}}+\left(\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right){s} \\ $$$${eqn}.\:{of}\:{AE}: \\ $$$${y}=\sqrt{\mathrm{3}}{x} \\ $$$${y}_{{M}} =\sqrt{\mathrm{3}}{x}_{{M}} =\frac{{x}_{{M}} }{\:\sqrt{\mathrm{3}}}+\left(\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right){s} \\ $$$$\Rightarrow{x}_{{M}} =\frac{\left(\sqrt{\mathrm{3}}−\mathrm{1}\right){s}}{\mathrm{2}} \\ $$$${eqn}.\:{of}\:{BE}: \\ $$$${y}=−\sqrt{\mathrm{3}}\left({x}−{s}\right) \\ $$$${y}_{{N}} =−\sqrt{\mathrm{3}}\left({x}_{{N}} −{s}\right)=\frac{{x}_{{N}} }{\:\sqrt{\mathrm{3}}}+\left(\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right){s} \\ $$$$\Rightarrow{x}_{{N}} =\frac{\left(\mathrm{4}−\sqrt{\mathrm{3}}\right){s}}{\mathrm{4}} \\ $$$$\Delta{x}_{{MJ}} ={x}_{{M}} −{x}_{{J}} =\frac{\left(\sqrt{\mathrm{3}}−\mathrm{1}\right){s}}{\mathrm{2}} \\ $$$$\Delta{x}_{{CN}} ={x}_{{C}} −{x}_{{N}} ={s}−\frac{\left(\mathrm{4}−\sqrt{\mathrm{3}}\right){s}}{\mathrm{4}}=\frac{\sqrt{\mathrm{3}}{s}}{\mathrm{4}} \\ $$$$\Delta{x}_{{NM}} ={x}_{{N}} −{x}_{{M}} =\frac{\left(\mathrm{4}−\sqrt{\mathrm{3}}\right){s}}{\mathrm{4}}−\frac{\left(\sqrt{\mathrm{3}}−\mathrm{1}\right){s}}{\mathrm{2}}=\frac{\mathrm{3}\left(\mathrm{2}−\sqrt{\mathrm{3}}\right){s}}{\mathrm{4}} \\ $$$$\frac{{c}−{a}}{{b}}=\frac{\Delta{x}_{{CN}} −\Delta{x}_{{MJ}} }{\Delta{x}_{{MN}} } \\ $$$$\:\:\:\:\:\:\:=\frac{\frac{\sqrt{\mathrm{3}}{s}}{\mathrm{4}}−\frac{\left(\sqrt{\mathrm{3}}−\mathrm{1}\right){s}}{\mathrm{2}}}{\frac{\mathrm{3}\left(\mathrm{2}−\sqrt{\mathrm{3}}\right){s}}{\mathrm{4}}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow{b}=\mathrm{3}\left({c}−{a}\right)\:\checkmark \\ $$

Commented by Spillover last updated on 13/Apr/25

great.thank you

$${great}.{thank}\:{you} \\ $$

Answered by Spillover last updated on 17/Apr/25

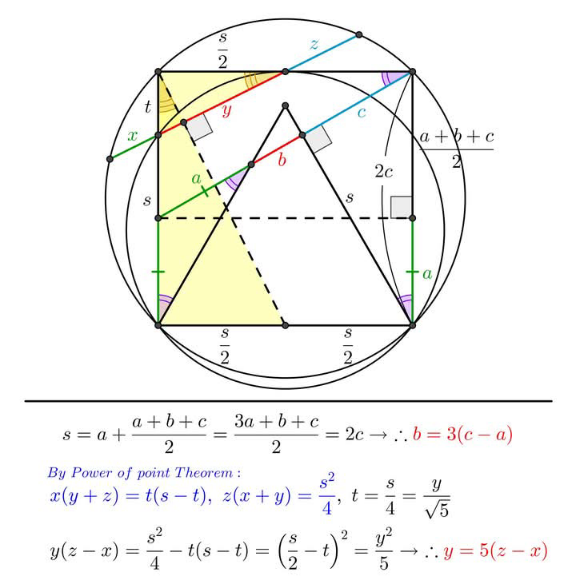
Answered by Spillover last updated on 17/Apr/25

Terms of Service

Privacy Policy

Contact: info@tinkutara.com