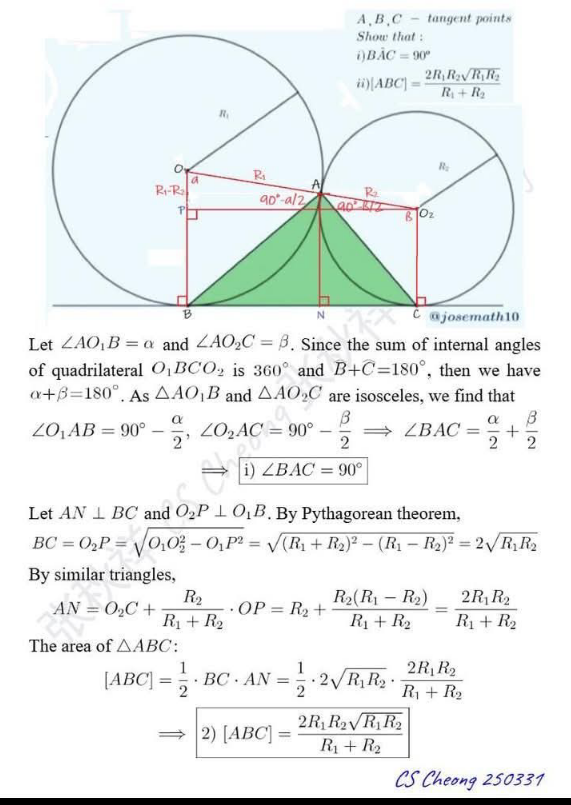
Question Number 218606 by Spillover last updated on 12/Apr/25
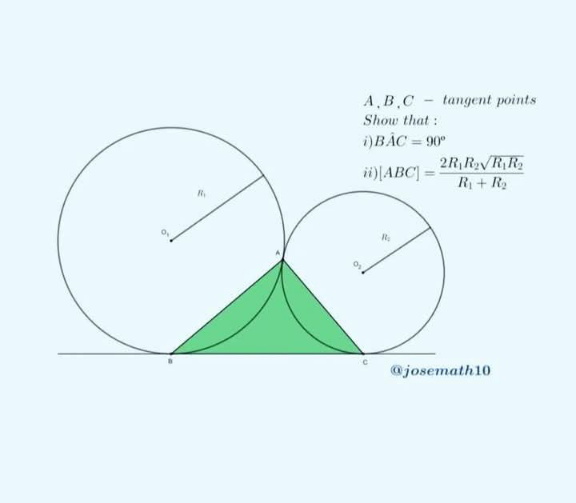
Answered by A5T last updated on 13/Apr/25
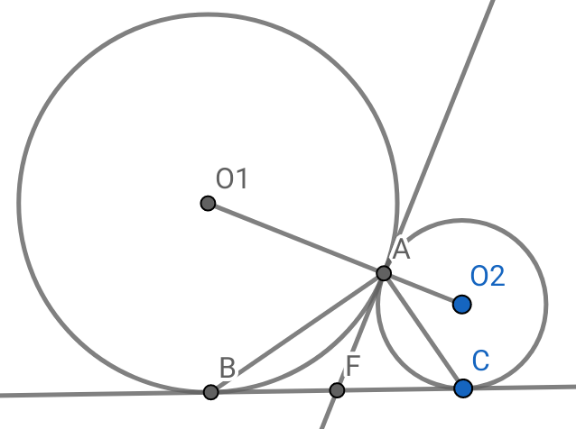
Commented by A5T last updated on 13/Apr/25
![∠BAF=α ⇒ ∠ABF=α since BF=AF Similarly ∠CAF=∠AFC=β since AF=FC ∠ABC+∠BCA+∠CAB=180° ⇒ 2(α+β)=180° ⇒α+β=90°=∠BAC sin∠BO_1 O_2 =((√((R+r)^2 −(R−r)^2 ))/(R+r))=((2(√(Rr)))/(R+r)) sin∠AO_2 C=((2(√(Rr)))/(R+r)) [ABC]=((2(R+r)(√(Rr)))/2)−((R^2 (√(Rr)))/(R+r))−((r^2 (√(Rr)))/(R+r)) ⇒[ABC]=(([(R+r)^2 −R^2 −r^2 ](√(Rr)))/(R+r))=((2Rr(√(Rr)))/(R+r))](Q218614.png)
$$\angle\mathrm{BAF}=\alpha\:\Rightarrow\:\angle\mathrm{ABF}=\alpha\:\mathrm{since}\:\mathrm{BF}=\mathrm{AF} \\ $$$$\mathrm{Similarly}\:\angle\mathrm{CAF}=\angle\mathrm{AFC}=\beta\:\mathrm{since}\:\mathrm{AF}=\mathrm{FC} \\ $$$$\angle\mathrm{ABC}+\angle\mathrm{BCA}+\angle\mathrm{CAB}=\mathrm{180}°\:\Rightarrow\:\mathrm{2}\left(\alpha+\beta\right)=\mathrm{180}° \\ $$$$\Rightarrow\alpha+\beta=\mathrm{90}°=\angle\mathrm{BAC} \\ $$$$\mathrm{sin}\angle\mathrm{BO}_{\mathrm{1}} \mathrm{O}_{\mathrm{2}} =\frac{\sqrt{\left(\mathrm{R}+\mathrm{r}\right)^{\mathrm{2}} −\left(\mathrm{R}−\mathrm{r}\right)^{\mathrm{2}} }}{\mathrm{R}+\mathrm{r}}=\frac{\mathrm{2}\sqrt{\mathrm{Rr}}}{\mathrm{R}+\mathrm{r}} \\ $$$$\mathrm{sin}\angle\mathrm{AO}_{\mathrm{2}} \mathrm{C}=\frac{\mathrm{2}\sqrt{\mathrm{Rr}}}{\mathrm{R}+\mathrm{r}} \\ $$$$\left[\mathrm{ABC}\right]=\frac{\mathrm{2}\left(\mathrm{R}+\mathrm{r}\right)\sqrt{\mathrm{Rr}}}{\mathrm{2}}−\frac{\mathrm{R}^{\mathrm{2}} \sqrt{\mathrm{Rr}}}{\mathrm{R}+\mathrm{r}}−\frac{\mathrm{r}^{\mathrm{2}} \sqrt{\mathrm{Rr}}}{\mathrm{R}+\mathrm{r}} \\ $$$$\Rightarrow\left[\mathrm{ABC}\right]=\frac{\left[\left(\mathrm{R}+\mathrm{r}\right)^{\mathrm{2}} −\mathrm{R}^{\mathrm{2}} −\mathrm{r}^{\mathrm{2}} \right]\sqrt{\mathrm{Rr}}}{\mathrm{R}+\mathrm{r}}=\frac{\mathrm{2Rr}\sqrt{\mathrm{Rr}}}{\mathrm{R}+\mathrm{r}} \\ $$
Commented by Spillover last updated on 13/Apr/25

$${correct} \\ $$
Answered by mr W last updated on 13/Apr/25
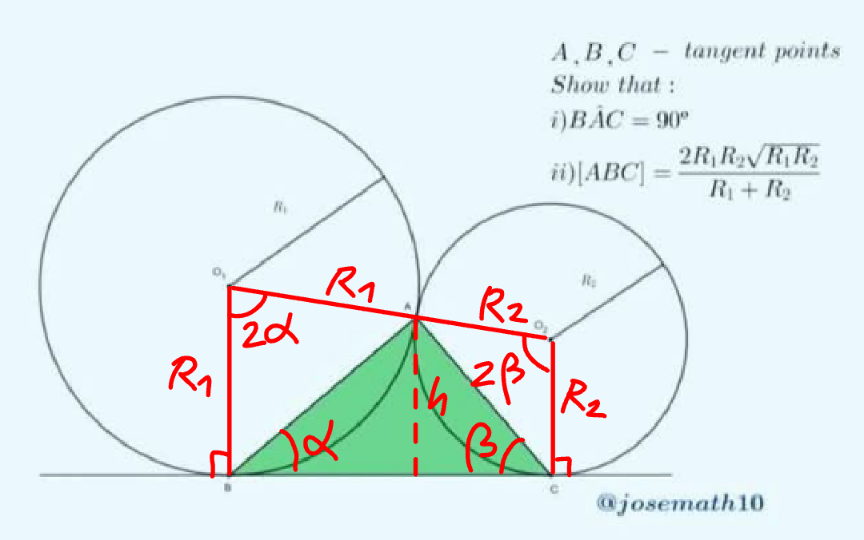
Commented by mr W last updated on 13/Apr/25
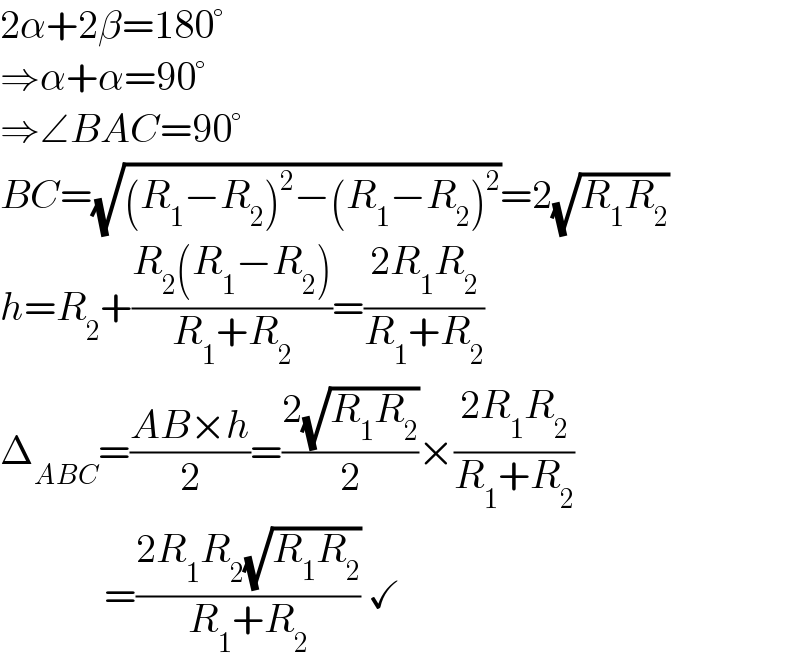
$$\mathrm{2}\alpha+\mathrm{2}\beta=\mathrm{180}° \\ $$$$\Rightarrow\alpha+\alpha=\mathrm{90}° \\ $$$$\Rightarrow\angle{BAC}=\mathrm{90}° \\ $$$${BC}=\sqrt{\left({R}_{\mathrm{1}} −{R}_{\mathrm{2}} \right)^{\mathrm{2}} −\left({R}_{\mathrm{1}} −{R}_{\mathrm{2}} \right)^{\mathrm{2}} }=\mathrm{2}\sqrt{{R}_{\mathrm{1}} {R}_{\mathrm{2}} } \\ $$$${h}={R}_{\mathrm{2}} +\frac{{R}_{\mathrm{2}} \left({R}_{\mathrm{1}} −{R}_{\mathrm{2}} \right)}{{R}_{\mathrm{1}} +{R}_{\mathrm{2}} }=\frac{\mathrm{2}{R}_{\mathrm{1}} {R}_{\mathrm{2}} }{{R}_{\mathrm{1}} +{R}_{\mathrm{2}} } \\ $$$$\Delta_{{ABC}} =\frac{{AB}×{h}}{\mathrm{2}}=\frac{\mathrm{2}\sqrt{{R}_{\mathrm{1}} {R}_{\mathrm{2}} }}{\mathrm{2}}×\frac{\mathrm{2}{R}_{\mathrm{1}} {R}_{\mathrm{2}} }{{R}_{\mathrm{1}} +{R}_{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{2}{R}_{\mathrm{1}} {R}_{\mathrm{2}} \sqrt{{R}_{\mathrm{1}} {R}_{\mathrm{2}} }}{{R}_{\mathrm{1}} +{R}_{\mathrm{2}} }\:\checkmark \\ $$
Commented by Spillover last updated on 13/Apr/25

$${correct} \\ $$
Answered by Spillover last updated on 13/Apr/25