Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

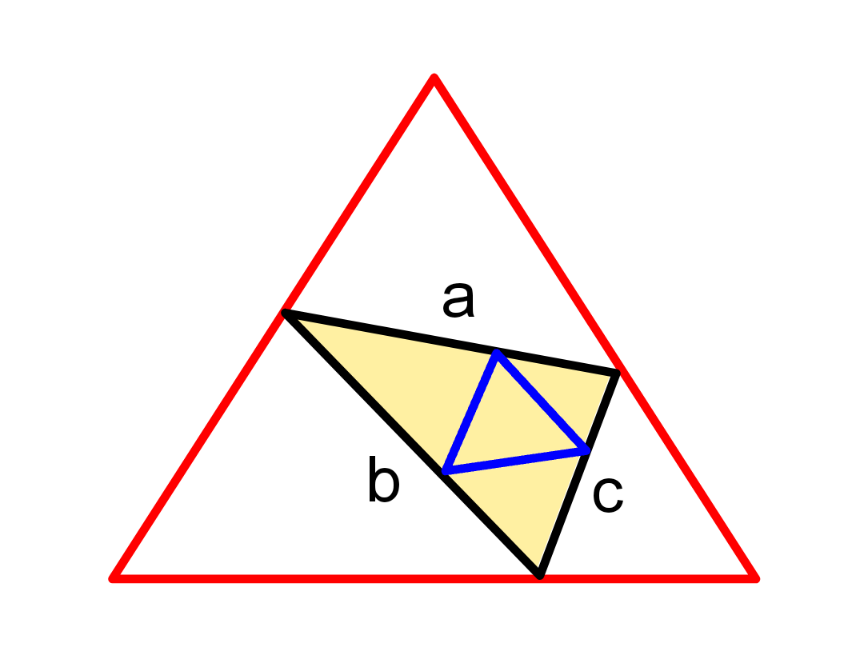
Question Number 218580 by mr W last updated on 12/Apr/25

Commented by vnm last updated on 12/Apr/25

Let triangle ABC be inscribed in equilateral triangle DEF. The area of DEF is maximal if there exists a point G inside ABC such that GA, GB, GC are perpendicular to EF, FD, DE. let BC=a, CA=b, AB=c GA=x, GB=y, GC=z ∠BGC=∠CGA=∠AGB=((2π)/3) { ((y^2 +z^2 +yz=a^2 )),((z^2 +x^2 +zx=b^2 )),((x^2 +y^2 +xy=c^2 )) :} y^2 −x^2 +z(y−x)=a^2 −b^2 (x+y+z)(y−x)=a^2 −b^2 (x+y+z)(z−x)=a^2 −c^2 x+y+z=w x−y=((b^2 −a^2 )/w), x−z=((c^2 −a^2 )/w) x=(1/3)(w+((b^2 +c^2 −2a^2 )/w)) y=(1/3)(w+((c^2 +a^2 −2b^2 )/w)) z=(1/3)(w+((a^2 +b^2 −2c^2 )/w)) x^2 +y^2 +xy=c^2 ................................. (w^2 )^2 −w^2 (a^2 +b^2 +c^2 )+ (a^4 +b^4 +c^4 −b^2 c^2 −c^2 a^2 −a^2 b^2 )=0 w^2 =((a^2 +b^2 +c^2 +(√(3(2(b^2 c^2 +c^2 a^2 +a^2 b^2 )−a^4 −b^4 −c^4 ))))/2) In an equilateral triangle the sum of the distances from any point to the sides is a constant value and is equal to the altitude of the triangle, w is the altitude. S_(△DEF) =(w^2 /( (√3)))=((a^2 +b^2 +c^2 +(√(3(2(b^2 c^2 +c^2 a^2 +a^2 b^2 )−a^4 −b^4 −c^4 ))))/(2(√3)))

$$ \\ $$$$\mathrm{Let}\:\mathrm{triangle}\:\mathrm{ABC}\:\mathrm{be}\:\mathrm{inscribed}\:\mathrm{in}\:\mathrm{equilateral}\:\mathrm{triangle}\:\mathrm{DEF}. \\ $$$$\mathrm{The}\:\mathrm{area}\:\mathrm{of}\:\mathrm{DEF}\:\mathrm{is}\:\mathrm{maximal}\: \\ $$$$\mathrm{if}\:\mathrm{there}\:\mathrm{exists}\:\mathrm{a}\:\mathrm{point}\:\mathrm{G}\:\mathrm{inside}\:\mathrm{ABC}\:\mathrm{such}\:\mathrm{that}\:\mathrm{GA},\:\mathrm{GB},\:\mathrm{GC}\:\mathrm{are}\:\mathrm{perpendicular}\: \\ $$$$\mathrm{to}\:\mathrm{EF},\:\mathrm{FD},\:\mathrm{DE}. \\ $$$$\mathrm{let}\:{BC}={a},\:{CA}={b},\:{AB}={c} \\ $$$${GA}={x},\:{GB}={y},\:{GC}={z} \\ $$$$\angle{BGC}=\angle{CGA}=\angle{AGB}=\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$$$\begin{cases}{{y}^{\mathrm{2}} +{z}^{\mathrm{2}} +{yz}={a}^{\mathrm{2}} }\\{{z}^{\mathrm{2}} +{x}^{\mathrm{2}} +{zx}={b}^{\mathrm{2}} }\\{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{xy}={c}^{\mathrm{2}} }\end{cases} \\ $$$${y}^{\mathrm{2}} −{x}^{\mathrm{2}} +{z}\left({y}−{x}\right)={a}^{\mathrm{2}} −{b}^{\mathrm{2}} \\ $$$$\left({x}+{y}+{z}\right)\left({y}−{x}\right)={a}^{\mathrm{2}} −{b}^{\mathrm{2}} \\ $$$$\left({x}+{y}+{z}\right)\left({z}−{x}\right)={a}^{\mathrm{2}} −{c}^{\mathrm{2}} \\ $$$${x}+{y}+{z}={w} \\ $$$${x}−{y}=\frac{{b}^{\mathrm{2}} −{a}^{\mathrm{2}} }{{w}},\:\:\:{x}−{z}=\frac{{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }{{w}} \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{3}}\left({w}+\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{a}^{\mathrm{2}} }{{w}}\right) \\ $$$${y}=\frac{\mathrm{1}}{\mathrm{3}}\left({w}+\frac{{c}^{\mathrm{2}} +{a}^{\mathrm{2}} −\mathrm{2}{b}^{\mathrm{2}} }{{w}}\right) \\ $$$${z}=\frac{\mathrm{1}}{\mathrm{3}}\left({w}+\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{c}^{\mathrm{2}} }{{w}}\right) \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{xy}={c}^{\mathrm{2}} \\ $$$$................................. \\ $$$$\left({w}^{\mathrm{2}} \right)^{\mathrm{2}} −{w}^{\mathrm{2}} \left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)+ \\ $$$$\left({a}^{\mathrm{4}} +{b}^{\mathrm{4}} +{c}^{\mathrm{4}} −{b}^{\mathrm{2}} {c}^{\mathrm{2}} −{c}^{\mathrm{2}} {a}^{\mathrm{2}} −{a}^{\mathrm{2}} {b}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$${w}^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +\sqrt{\mathrm{3}\left(\mathrm{2}\left({b}^{\mathrm{2}} {c}^{\mathrm{2}} +{c}^{\mathrm{2}} {a}^{\mathrm{2}} +{a}^{\mathrm{2}} {b}^{\mathrm{2}} \right)−{a}^{\mathrm{4}} −{b}^{\mathrm{4}} −{c}^{\mathrm{4}} \right)}}{\mathrm{2}} \\ $$$$\mathrm{In}\:\mathrm{an}\:\mathrm{equilateral}\:\mathrm{triangle}\:\mathrm{the}\: \\ $$$$\mathrm{sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{distances}\:\mathrm{from}\:\mathrm{any} \\ $$$$\mathrm{point}\:\mathrm{to}\:\mathrm{the}\:\mathrm{sides}\:\mathrm{is}\:\mathrm{a}\:\mathrm{constant} \\ $$$$\mathrm{value}\:\mathrm{and}\:\mathrm{is}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{the}\:\mathrm{altitude}\:\mathrm{of}\:\mathrm{the}\:\mathrm{triangle},\:{w}\:\mathrm{is}\:\mathrm{the}\:\mathrm{altitude}. \\ $$$${S}_{\bigtriangleup{DEF}} =\frac{{w}^{\mathrm{2}} }{\:\sqrt{\mathrm{3}}}=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +\sqrt{\mathrm{3}\left(\mathrm{2}\left({b}^{\mathrm{2}} {c}^{\mathrm{2}} +{c}^{\mathrm{2}} {a}^{\mathrm{2}} +{a}^{\mathrm{2}} {b}^{\mathrm{2}} \right)−{a}^{\mathrm{4}} −{b}^{\mathrm{4}} −{c}^{\mathrm{4}} \right)}}{\mathrm{2}\sqrt{\mathrm{3}}} \\ $$

Commented by mr W last updated on 12/Apr/25

for a given triangle with sides a,b,c, 1) find the area of the largest equilateral triangle which can circumscribe it. (red in figure) 2) find the smallest equilateral triangle which can be inscribed in it. (blue in figure)

$${for}\:{a}\:{given}\:{triangle}\:{with}\:{sides}\:{a},{b},{c}, \\ $$$$\left.\mathrm{1}\right)\:{find}\:{the}\:{area}\:{of}\:{the}\:{largest}\: \\ $$$$\:\:\:\:\:\:{equilateral}\:{triangle}\:{which}\:{can}\: \\ $$$$\:\:\:\:\:\:{circumscribe}\:{it}.\:\left(\boldsymbol{{red}}\:{in}\:{figure}\right) \\ $$$$\left.\mathrm{2}\right)\:{find}\:{the}\:{smallest}\:{equilateral} \\ $$$$\:\:\:\:\:\:{triangle}\:{which}\:{can}\:{be}\:{inscribed} \\ $$$$\:\:\:\:\:\:{in}\:{it}.\:\left(\boldsymbol{{blue}}\:{in}\:{figure}\right) \\ $$

Commented by mr W last updated on 13/Apr/25

thansk! perfectly solved! considering heron′s formula, the result can also be expressed as ((a^2 +b^2 +c^2 )/(2(√3)))+2Δ with Δ=area of triangle ABC

$${thansk}! \\ $$$${perfectly}\:{solved}! \\ $$$${considering}\:{heron}'{s}\:{formula},\:{the} \\ $$$${result}\:{can}\:{also}\:{be}\:{expressed}\:{as} \\ $$$$\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{2}\sqrt{\mathrm{3}}}+\mathrm{2}\Delta \\ $$$${with}\:\Delta={area}\:{of}\:{triangle}\:{ABC} \\ $$

Answered by vnm last updated on 18/Apr/25

An algorithm for finding the area of the blue triangle. Triangle ABC: a=BC, b=CA, c=AB α=arccos((b^2 +c^2 −a^2 )/(2bc)), β=arccos((c^2 +a^2 −b^2 )/(2ca)), γ=arccos((a^2 +b^2 −c^2 )/(2ab)) α_1 =π−α, β_1 =π−β, γ_1 =π−γ PQR is an equilateral triangle with side length=1 point M inside PQR, such that α_1 =∠QMR, β_1 =∠RMP, γ_1 =∠PMQ p=MP, q=MQ, r=MR ϕ_α =∠MQR=((π−α_1 )/2)−δ, θ_α =∠MRQ=((π−α_1 )/2)+δ (r/(sinϕ_α ))=(1/(sinα_1 ))=(q/(sinθ_α )) q=((sinθ_α )/(sinα_1 )), r=((sinϕ_α )/(sinα_1 ))n θ_γ =∠MQP=(π/3)−ϕ_α = (π/3)−(((π−α_1 )/2)−δ)=(α_1 /2)−(π/6)+δ ϕ_β =∠MRP=(π/3)−θ_α = (π/3)−(((π−α_1 )/2)+δ)=(α_1 /2)−(π/6)−δ (p/(sinθ_γ ))=(1/(sinγ_1 )), p=((sinθ_γ )/(sinγ_1 )) (p/(sinϕ_β ))=(1/(sinβ_1 )), p=((sinϕ_β )/(sinβ_1 )) ((sinθ_γ )/(sinγ_1 ))=((sinϕ_β )/(sinβ_1 )), sinβ_1 ∙sinθ_γ =sinγ_1 ∙sinϕ_β sinβ_1 ∙sin((α_1 /2)−(π/6)+δ)=sinγ_1 ∙sin((α_1 /2)−(π/6)−δ) sinβ_1 (sin((3α_1 −π)/6)cosδ+cos((3α_1 −π)/6)sinδ)= sinγ_1 (sin((3α_1 −π)/6)cosδ−cos((3α_1 −π)/6)sinδ (sinγ_1 −sinβ_1 )tan((3α_1 −π)/6)=(sinγ_1 +sinβ_1 )tanδ δ=arctan(((sinγ_1 −sinβ_1 )/(sinγ_1 +sinβ_1 ))tan((3α_1 −π)/6)) Now we can calculate p, q, r. Draw lines perpendicular toMP, MQ, MR through points P, Q, R. The points F, G, H where these lines intersect are the vertices of a triangle similar to triangle ABC. f=GH=(1/2)((p+q)tan(γ_1 /2)+(q−p)cot(γ_1 /2))+(1/2)((p+r)tan(β_1 /2)+(r−p)cot(β_1 /2)) g=HF=(1/2)((q+r)tan(α_1 /2)+(r−q)cot(α_1 /2))+(1/2)((q+p)tan(γ_1 /2)+(p−q)cot(γ_1 /2)) h=FG=(1/2)((r+p)tan(β_1 /2)+(p−r)cot(β_1 /2))+(1/2)((r+q)tan(α_1 /2)+(q−r)cot(α_1 /2)) △PQR is the minimal equilateral triangle inscribed in △FGH. Answer: S_(△min.equilat) =S_(△ABC) (S_(△PQR) /S_(△FGH) )=(((√3)S_(△ABC) )/(4S_(△FGH) )) for example a=17, b=13, c=11 S_(△ABC) =71.4995629357271 p=0.368961052327 q=0.689772071985 r=0.721618806573 f=2.755346135575 g=2.107029397793 h=1.782871028902 (f/a)=(g/b)=(h/c)=0.162079184446 S_(△min.equilat) =16.483375438503

$$ \\ $$$${An}\:{algorithm}\:{for}\:{finding}\:{the} \\ $$$${area}\:{of}\:{the}\:{blue}\:{triangle}. \\ $$$${Triangle}\:{ABC}:\:{a}={BC},\:{b}={CA},\:{c}={AB} \\ $$$$\alpha=\mathrm{arccos}\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{bc}},\:\:\beta=\mathrm{arccos}\frac{{c}^{\mathrm{2}} +{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\mathrm{2}{ca}},\:\:\gamma=\mathrm{arccos}\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} }{\mathrm{2}{ab}} \\ $$$$\alpha_{\mathrm{1}} =\pi−\alpha,\:\:\beta_{\mathrm{1}} =\pi−\beta,\:\:\gamma_{\mathrm{1}} =\pi−\gamma \\ $$$${PQR}\:{is}\:{an}\:{equilateral}\:{triangle}\:{with}\:{side}\:{length}=\mathrm{1} \\ $$$${point}\:{M}\:{inside}\:{PQR},\:{such}\:{that} \\ $$$$\alpha_{\mathrm{1}} =\angle{QMR},\:\:\beta_{\mathrm{1}} =\angle{RMP},\:\:\gamma_{\mathrm{1}} =\angle{PMQ} \\ $$$${p}={MP},\:\:{q}={MQ},\:\:{r}={MR} \\ $$$$\varphi_{\alpha} =\angle{MQR}=\frac{\pi−\alpha_{\mathrm{1}} }{\mathrm{2}}−\delta,\:\:\theta_{\alpha} =\angle{MRQ}=\frac{\pi−\alpha_{\mathrm{1}} }{\mathrm{2}}+\delta \\ $$$$\frac{{r}}{\mathrm{sin}\varphi_{\alpha} }=\frac{\mathrm{1}}{\mathrm{sin}\alpha_{\mathrm{1}} }=\frac{{q}}{\mathrm{sin}\theta_{\alpha} } \\ $$$${q}=\frac{\mathrm{sin}\theta_{\alpha} }{\mathrm{sin}\alpha_{\mathrm{1}} },\:\:{r}=\frac{\mathrm{sin}\varphi_{\alpha} }{\mathrm{sin}\alpha_{\mathrm{1}} }{n} \\ $$$$\theta_{\gamma} =\angle{MQP}=\frac{\pi}{\mathrm{3}}−\varphi_{\alpha} = \\ $$$$\frac{\pi}{\mathrm{3}}−\left(\frac{\pi−\alpha_{\mathrm{1}} }{\mathrm{2}}−\delta\right)=\frac{\alpha_{\mathrm{1}} }{\mathrm{2}}−\frac{\pi}{\mathrm{6}}+\delta \\ $$$$\varphi_{\beta} =\angle{MRP}=\frac{\pi}{\mathrm{3}}−\theta_{\alpha} = \\ $$$$\frac{\pi}{\mathrm{3}}−\left(\frac{\pi−\alpha_{\mathrm{1}} }{\mathrm{2}}+\delta\right)=\frac{\alpha_{\mathrm{1}} }{\mathrm{2}}−\frac{\pi}{\mathrm{6}}−\delta \\ $$$$\frac{{p}}{\mathrm{sin}\theta_{\gamma} }=\frac{\mathrm{1}}{\mathrm{sin}\gamma_{\mathrm{1}} },\:\:{p}=\frac{\mathrm{sin}\theta_{\gamma} }{\mathrm{sin}\gamma_{\mathrm{1}} } \\ $$$$\frac{{p}}{\mathrm{sin}\varphi_{\beta} }=\frac{\mathrm{1}}{\mathrm{sin}\beta_{\mathrm{1}} },\:\:{p}=\frac{\mathrm{sin}\varphi_{\beta} }{\mathrm{sin}\beta_{\mathrm{1}} } \\ $$$$\frac{\mathrm{sin}\theta_{\gamma} }{\mathrm{sin}\gamma_{\mathrm{1}} }=\frac{\mathrm{sin}\varphi_{\beta} }{\mathrm{sin}\beta_{\mathrm{1}} },\:\:\mathrm{sin}\beta_{\mathrm{1}} \centerdot\mathrm{sin}\theta_{\gamma} =\mathrm{sin}\gamma_{\mathrm{1}} \centerdot\mathrm{sin}\varphi_{\beta} \\ $$$$\mathrm{sin}\beta_{\mathrm{1}} \centerdot\mathrm{sin}\left(\frac{\alpha_{\mathrm{1}} }{\mathrm{2}}−\frac{\pi}{\mathrm{6}}+\delta\right)=\mathrm{sin}\gamma_{\mathrm{1}} \centerdot\mathrm{sin}\left(\frac{\alpha_{\mathrm{1}} }{\mathrm{2}}−\frac{\pi}{\mathrm{6}}−\delta\right) \\ $$$$\mathrm{sin}\beta_{\mathrm{1}} \left(\mathrm{sin}\frac{\mathrm{3}\alpha_{\mathrm{1}} −\pi}{\mathrm{6}}\mathrm{cos}\delta+\mathrm{cos}\frac{\mathrm{3}\alpha_{\mathrm{1}} −\pi}{\mathrm{6}}\mathrm{sin}\delta\right)= \\ $$$$\mathrm{sin}\gamma_{\mathrm{1}} \left(\mathrm{sin}\frac{\mathrm{3}\alpha_{\mathrm{1}} −\pi}{\mathrm{6}}\mathrm{cos}\delta−\mathrm{cos}\frac{\mathrm{3}\alpha_{\mathrm{1}} −\pi}{\mathrm{6}}\mathrm{sin}\delta\right. \\ $$$$\left(\mathrm{sin}\gamma_{\mathrm{1}} −\mathrm{sin}\beta_{\mathrm{1}} \right)\mathrm{tan}\frac{\mathrm{3}\alpha_{\mathrm{1}} −\pi}{\mathrm{6}}=\left(\mathrm{sin}\gamma_{\mathrm{1}} +\mathrm{sin}\beta_{\mathrm{1}} \right)\mathrm{tan}\delta \\ $$$$\delta=\mathrm{arctan}\left(\frac{\mathrm{sin}\gamma_{\mathrm{1}} −\mathrm{sin}\beta_{\mathrm{1}} }{\mathrm{sin}\gamma_{\mathrm{1}} +\mathrm{sin}\beta_{\mathrm{1}} }\mathrm{tan}\frac{\mathrm{3}\alpha_{\mathrm{1}} −\pi}{\mathrm{6}}\right) \\ $$$${Now}\:{we}\:{can}\:{calculate}\:{p},\:{q},\:{r}. \\ $$$${Draw}\:{lines}\:{perpendicular}\:{toMP},\:{MQ},\:{MR}\: \\ $$$${through}\:{points}\:{P},\:{Q},\:{R}. \\ $$$${The}\:{points}\:{F},\:{G},\:{H}\:{where}\:{these} \\ $$$${lines}\:{intersect}\:{are}\:{the}\:{vertices}\: \\ $$$${of}\:{a}\:{triangle}\:{similar}\:{to}\:{triangle} \\ $$$${ABC}. \\ $$$${f}={GH}=\frac{\mathrm{1}}{\mathrm{2}}\left(\left({p}+{q}\right)\mathrm{tan}\frac{\gamma_{\mathrm{1}} }{\mathrm{2}}+\left({q}−{p}\right)\mathrm{cot}\frac{\gamma_{\mathrm{1}} }{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{2}}\left(\left({p}+{r}\right)\mathrm{tan}\frac{\beta_{\mathrm{1}} }{\mathrm{2}}+\left({r}−{p}\right)\mathrm{cot}\frac{\beta_{\mathrm{1}} }{\mathrm{2}}\right) \\ $$$${g}={HF}=\frac{\mathrm{1}}{\mathrm{2}}\left(\left({q}+{r}\right)\mathrm{tan}\frac{\alpha_{\mathrm{1}} }{\mathrm{2}}+\left({r}−{q}\right)\mathrm{cot}\frac{\alpha_{\mathrm{1}} }{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{2}}\left(\left({q}+{p}\right)\mathrm{tan}\frac{\gamma_{\mathrm{1}} }{\mathrm{2}}+\left({p}−{q}\right)\mathrm{cot}\frac{\gamma_{\mathrm{1}} }{\mathrm{2}}\right) \\ $$$${h}={FG}=\frac{\mathrm{1}}{\mathrm{2}}\left(\left({r}+{p}\right)\mathrm{tan}\frac{\beta_{\mathrm{1}} }{\mathrm{2}}+\left({p}−{r}\right)\mathrm{cot}\frac{\beta_{\mathrm{1}} }{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{2}}\left(\left({r}+{q}\right)\mathrm{tan}\frac{\alpha_{\mathrm{1}} }{\mathrm{2}}+\left({q}−{r}\right)\mathrm{cot}\frac{\alpha_{\mathrm{1}} }{\mathrm{2}}\right) \\ $$$$\bigtriangleup{PQR}\:{is}\:{the}\:{minimal}\:{equilateral}\:{triangle}\:{inscribed}\:{in}\:\bigtriangleup{FGH}. \\ $$$${Answer}: \\ $$$${S}_{\bigtriangleup{min}.{equilat}} ={S}_{\bigtriangleup{ABC}} \frac{{S}_{\bigtriangleup{PQR}} }{{S}_{\bigtriangleup{FGH}} }=\frac{\sqrt{\mathrm{3}}{S}_{\bigtriangleup{ABC}} }{\mathrm{4}{S}_{\bigtriangleup{FGH}} } \\ $$$${for}\:{example} \\ $$$${a}=\mathrm{17},\:{b}=\mathrm{13},\:{c}=\mathrm{11} \\ $$$${S}_{\bigtriangleup{ABC}} =\mathrm{71}.\mathrm{4995629357271} \\ $$$$\mathrm{p}=\mathrm{0}.\mathrm{368961052327} \\ $$$${q}=\mathrm{0}.\mathrm{689772071985} \\ $$$${r}=\mathrm{0}.\mathrm{721618806573} \\ $$$$\mathrm{f}=\mathrm{2}.\mathrm{755346135575} \\ $$$${g}=\mathrm{2}.\mathrm{107029397793} \\ $$$${h}=\mathrm{1}.\mathrm{782871028902} \\ $$$$\frac{{f}}{{a}}=\frac{{g}}{{b}}=\frac{{h}}{{c}}=\mathrm{0}.\mathrm{162079184446} \\ $$$${S}_{\bigtriangleup{min}.{equilat}} =\mathrm{16}.\mathrm{483375438503} \\ $$

Commented by mr W last updated on 20/Apr/25

thanks sir!

$${thanks}\:{sir}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com