Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

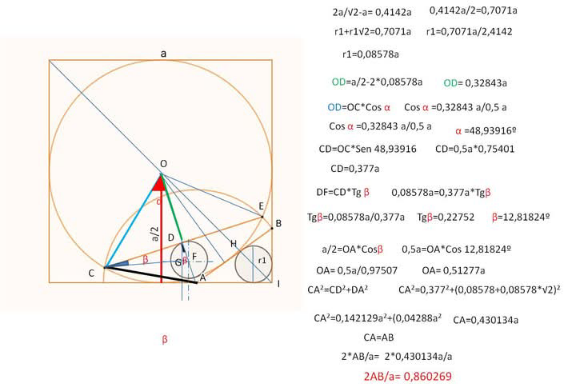
Question Number 218526 by Spillover last updated on 11/Apr/25

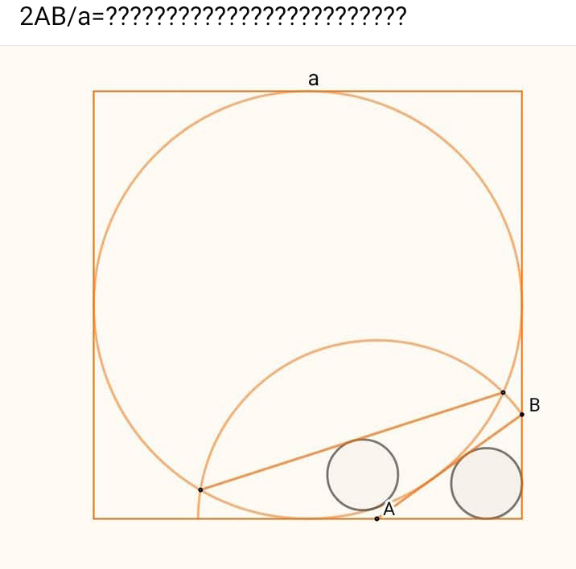
Commented by mr W last updated on 11/Apr/25

≈0.8348

$$\approx\mathrm{0}.\mathrm{8348} \\ $$

Commented by Spillover last updated on 11/Apr/25

correct

$${correct} \\ $$

Answered by mr W last updated on 11/Apr/25

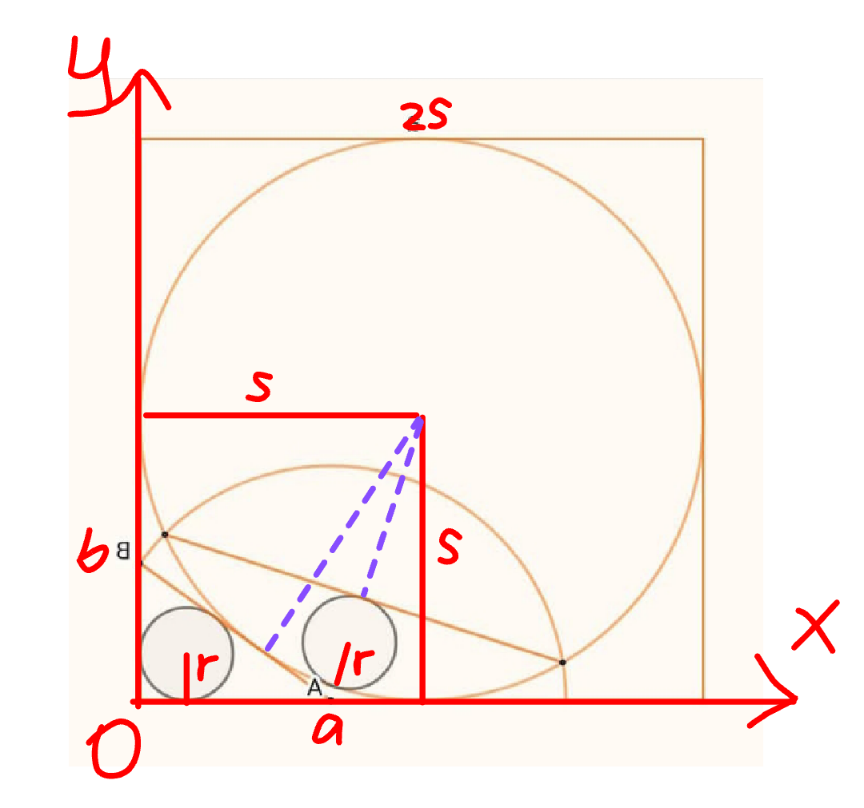
Commented by mr W last updated on 12/Apr/25

“a” in original question is replaced with 2s in following. say A(a,0), B(0,b) r=((ab)/(a+b+(√(a^2 +b^2 )))) (x/a)+(y/b)=1 or bx+ay=ab ← eqn. of AB s=((bs+as−ab)/( (√(a^2 +b^2 )))) (a+b−(√(a^2 +b^2 )))s=ab say α=(a/s), β=(b/s) α+β−(√(α^2 +β^2 ))=αβ β=((2(1−α))/(2−α)) ...(I) (x−a)^2 +y^2 =a^2 +b^2 x^2 −2ax+y^2 =b^2 ...(i) (x−s)^2 +(y−s)^2 =s^2 x^2 −2sx+y^2 −2sy=−s^2 ...(ii) (i)−(ii): 2(s−a)x+2sy=b^2 +s^2 ← eqn. of intersection line d=((2(s−a)s+2s^2 −b^2 −s^2 )/( 2(√((s−a)^2 +s^2 ))))=s−2r ((3s^2 −2as−b^2 )/( 2(√(2s^2 −2sa+a^2 ))))=s−((2ab)/(a+b+(√(a^2 +b^2 )))) ((3−2α−β^2 )/( 2(√(2−2α+α^2 ))))=1−((2αβ)/(α+β+(√(α^2 +β^2 )))) ...(II) from (I) and (II) we get α≈0.677 564 399 386, β≈0.487 639 020 704 ((2AB)/(“a”))=((AB)/s)=((√(a^2 +b^2 ))/s) =(√(α^2 +β^2 ))≈0.834 796 579 910 ✓

$$``{a}''\:{in}\:{original}\:{question}\:{is}\:{replaced} \\ $$$${with}\:\mathrm{2}{s}\:{in}\:{following}. \\ $$$${say}\:{A}\left({a},\mathrm{0}\right),\:{B}\left(\mathrm{0},{b}\right) \\ $$$${r}=\frac{{ab}}{{a}+{b}+\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }} \\ $$$$\frac{{x}}{{a}}+\frac{{y}}{{b}}=\mathrm{1}\:{or}\:{bx}+{ay}={ab}\:\:\:\leftarrow\:{eqn}.\:{of}\:{AB} \\ $$$${s}=\frac{{bs}+{as}−{ab}}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }} \\ $$$$\left({a}+{b}−\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\right){s}={ab} \\ $$$${say}\:\alpha=\frac{{a}}{{s}},\:\beta=\frac{{b}}{{s}} \\ $$$$\alpha+\beta−\sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} }=\alpha\beta \\ $$$$\beta=\frac{\mathrm{2}\left(\mathrm{1}−\alpha\right)}{\mathrm{2}−\alpha}\:\:\:...\left({I}\right) \\ $$$$ \\ $$$$\left({x}−{a}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} −\mathrm{2}{ax}+{y}^{\mathrm{2}} ={b}^{\mathrm{2}} \:\:\:...\left({i}\right) \\ $$$$\left({x}−{s}\right)^{\mathrm{2}} +\left({y}−{s}\right)^{\mathrm{2}} ={s}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} −\mathrm{2}{sx}+{y}^{\mathrm{2}} −\mathrm{2}{sy}=−{s}^{\mathrm{2}} \:\:\:...\left({ii}\right) \\ $$$$\left({i}\right)−\left({ii}\right): \\ $$$$\mathrm{2}\left({s}−{a}\right){x}+\mathrm{2}{sy}={b}^{\mathrm{2}} +{s}^{\mathrm{2}} \:\:\:\leftarrow\:{eqn}.\:{of}\:{intersection}\:{line} \\ $$$${d}=\frac{\mathrm{2}\left({s}−{a}\right){s}+\mathrm{2}{s}^{\mathrm{2}} −{b}^{\mathrm{2}} −{s}^{\mathrm{2}} }{\:\mathrm{2}\sqrt{\left({s}−{a}\right)^{\mathrm{2}} +{s}^{\mathrm{2}} }}={s}−\mathrm{2}{r} \\ $$$$\frac{\mathrm{3}{s}^{\mathrm{2}} −\mathrm{2}{as}−{b}^{\mathrm{2}} }{\:\mathrm{2}\sqrt{\mathrm{2}{s}^{\mathrm{2}} −\mathrm{2}{sa}+{a}^{\mathrm{2}} }}={s}−\frac{\mathrm{2}{ab}}{{a}+{b}+\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }} \\ $$$$\frac{\mathrm{3}−\mathrm{2}\alpha−\beta^{\mathrm{2}} }{\:\mathrm{2}\sqrt{\mathrm{2}−\mathrm{2}\alpha+\alpha^{\mathrm{2}} }}=\mathrm{1}−\frac{\mathrm{2}\alpha\beta}{\alpha+\beta+\sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} }}\:\:\:...\left({II}\right) \\ $$$$ \\ $$$${from}\:\left({I}\right)\:{and}\:\left({II}\right)\:{we}\:{get} \\ $$$$\alpha\approx\mathrm{0}.\mathrm{677}\:\mathrm{564}\:\mathrm{399}\:\mathrm{386},\:\beta\approx\mathrm{0}.\mathrm{487}\:\mathrm{639}\:\mathrm{020}\:\mathrm{704} \\ $$$$\frac{\mathrm{2}{AB}}{``{a}''}=\frac{{AB}}{{s}}=\frac{\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}{{s}} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} }\approx\mathrm{0}.\mathrm{834}\:\mathrm{796}\:\mathrm{579}\:\mathrm{910}\:\checkmark \\ $$

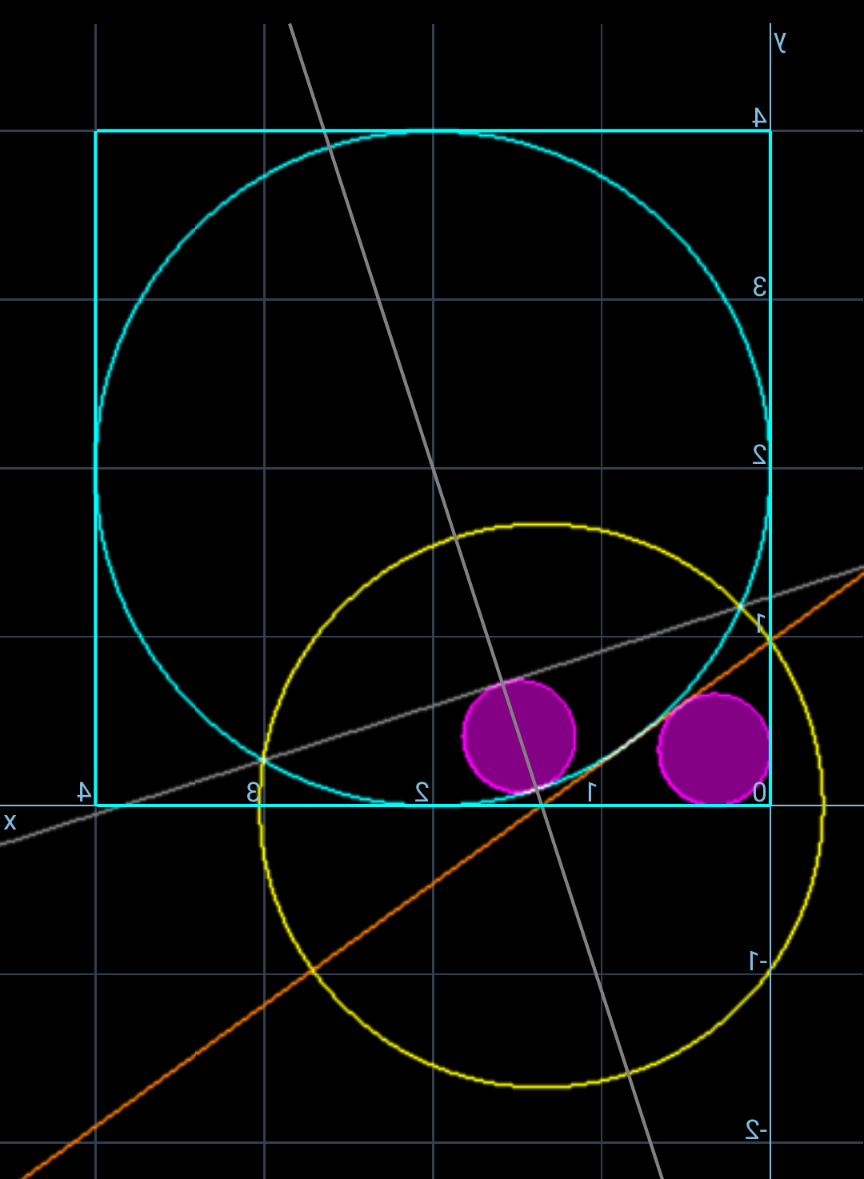
Commented by mr W last updated on 11/Apr/25

Commented by Spillover last updated on 17/Apr/25

GOD bless you.very?nice solution

$${GOD}\:{bless}\:{you}.{very}?{nice} \\ $$$${solution} \\ $$

Answered by Spillover last updated on 11/Apr/25

Terms of Service

Privacy Policy

Contact: info@tinkutara.com