
Question Number 218525 by Spillover last updated on 11/Apr/25
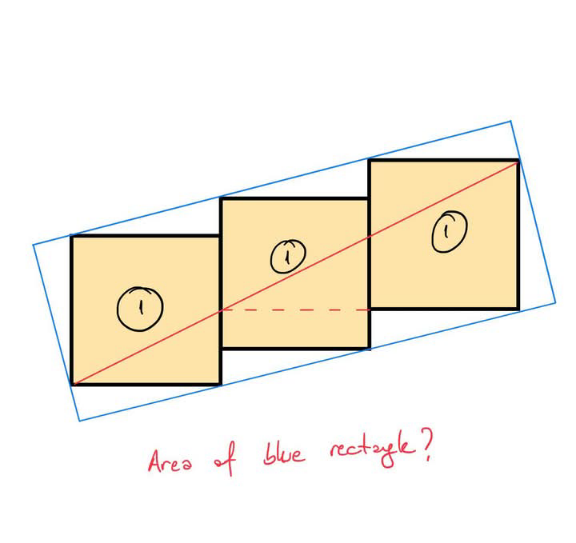
Answered by mr W last updated on 11/Apr/25
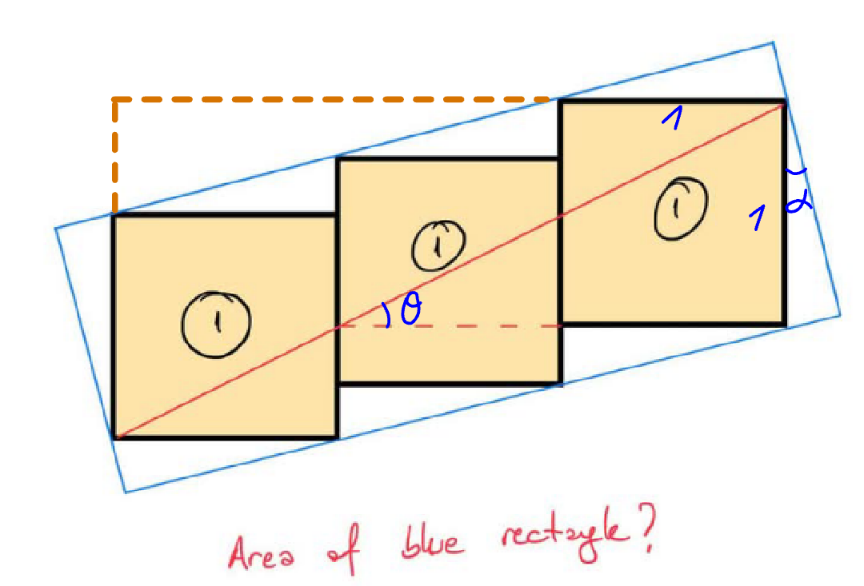
Commented by mr W last updated on 11/Apr/25
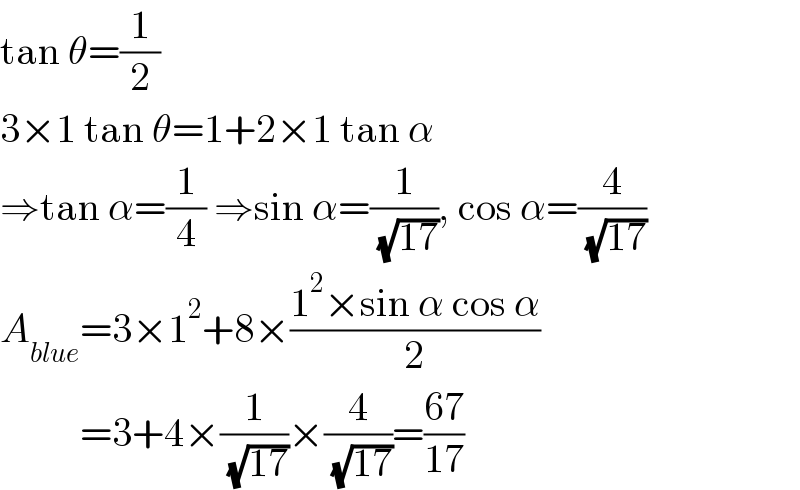
$$\mathrm{tan}\:\theta=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{3}×\mathrm{1}\:\mathrm{tan}\:\theta=\mathrm{1}+\mathrm{2}×\mathrm{1}\:\mathrm{tan}\:\alpha \\ $$$$\Rightarrow\mathrm{tan}\:\alpha=\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow\mathrm{sin}\:\alpha=\frac{\mathrm{1}}{\:\sqrt{\mathrm{17}}},\:\mathrm{cos}\:\alpha=\frac{\mathrm{4}}{\:\sqrt{\mathrm{17}}} \\ $$$${A}_{{blue}} =\mathrm{3}×\mathrm{1}^{\mathrm{2}} +\mathrm{8}×\frac{\mathrm{1}^{\mathrm{2}} ×\mathrm{sin}\:\alpha\:\mathrm{cos}\:\alpha}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\mathrm{3}+\mathrm{4}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{17}}}×\frac{\mathrm{4}}{\:\sqrt{\mathrm{17}}}=\frac{\mathrm{67}}{\mathrm{17}} \\ $$
Commented by Spillover last updated on 17/Apr/25
$${great}\:{thank}\:{you} \\ $$
