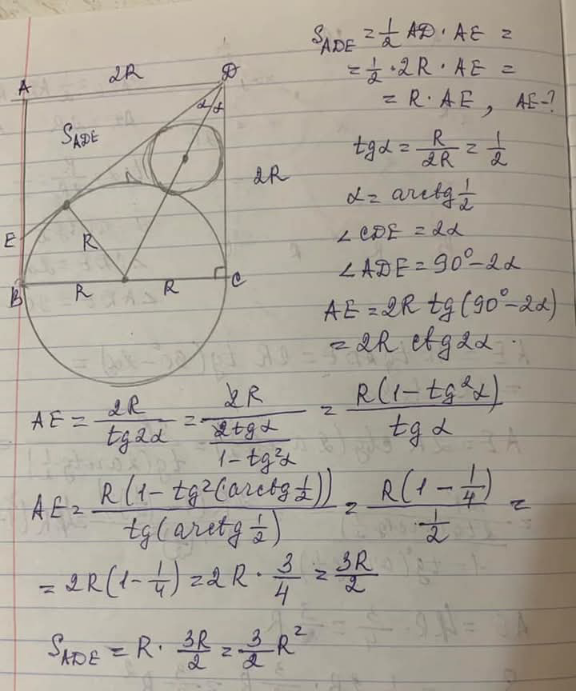Question Number 218494 by Spillover last updated on 10/Apr/25
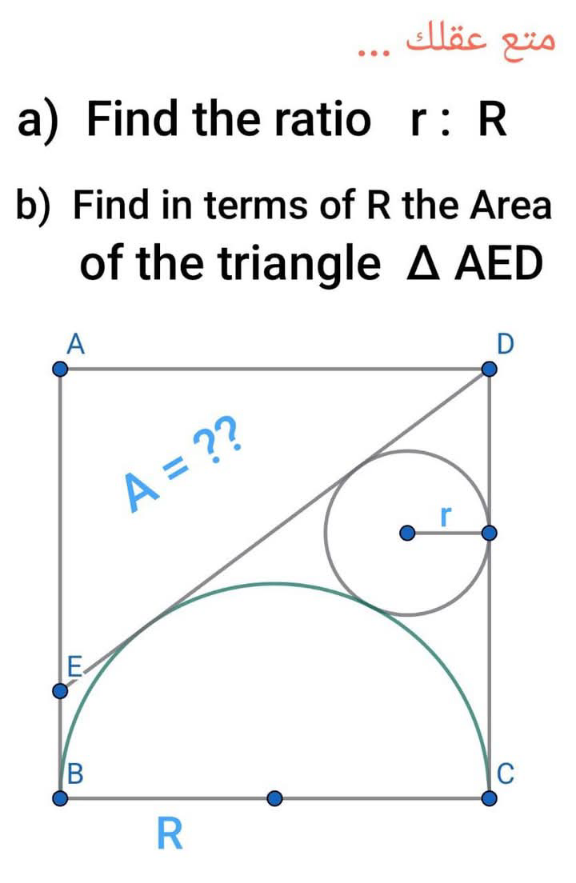
Answered by vnm last updated on 10/Apr/25
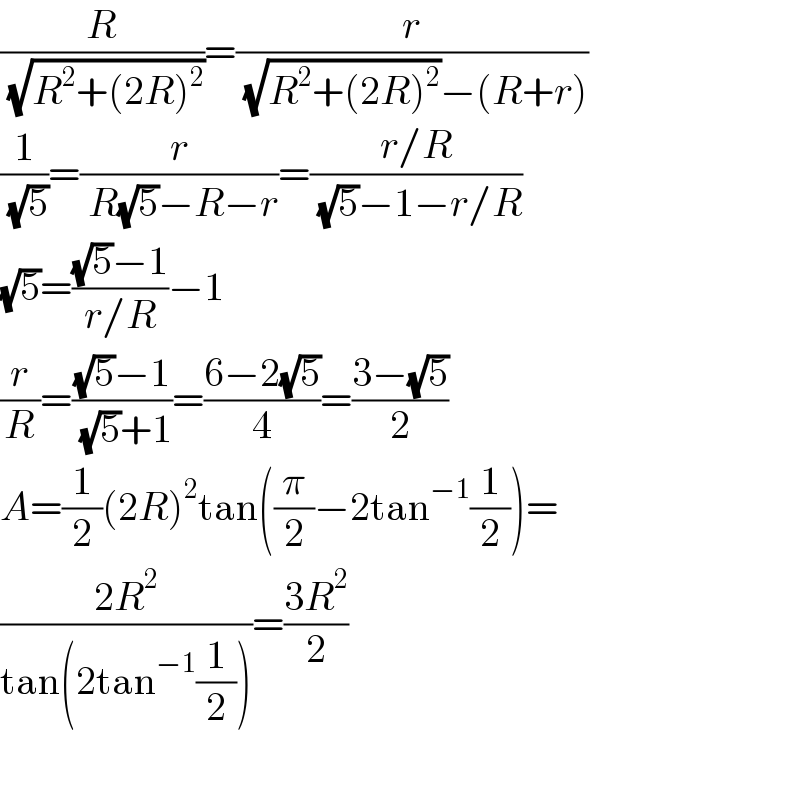
$$\frac{{R}}{\:\sqrt{{R}^{\mathrm{2}} +\left(\mathrm{2}{R}\right)^{\mathrm{2}} }}=\frac{{r}}{\:\sqrt{{R}^{\mathrm{2}} +\left(\mathrm{2}{R}\right)^{\mathrm{2}} }−\left({R}+{r}\right)} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}=\frac{{r}}{\:{R}\sqrt{\mathrm{5}}−{R}−{r}}=\frac{{r}/{R}}{\:\sqrt{\mathrm{5}}−\mathrm{1}−{r}/{R}} \\ $$$$\sqrt{\mathrm{5}}=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{{r}/{R}}−\mathrm{1} \\ $$$$\frac{{r}}{{R}}=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\:\sqrt{\mathrm{5}}+\mathrm{1}}=\frac{\mathrm{6}−\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{4}}=\frac{\mathrm{3}−\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$${A}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}{R}\right)^{\mathrm{2}} \mathrm{tan}\left(\frac{\pi}{\mathrm{2}}−\mathrm{2tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}\right)= \\ $$$$\frac{\mathrm{2}{R}^{\mathrm{2}} }{\mathrm{tan}\left(\mathrm{2tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}\right)}=\frac{\mathrm{3}{R}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$ \\ $$
Commented by Spillover last updated on 11/Apr/25

$${correct} \\ $$
Answered by mr W last updated on 10/Apr/25
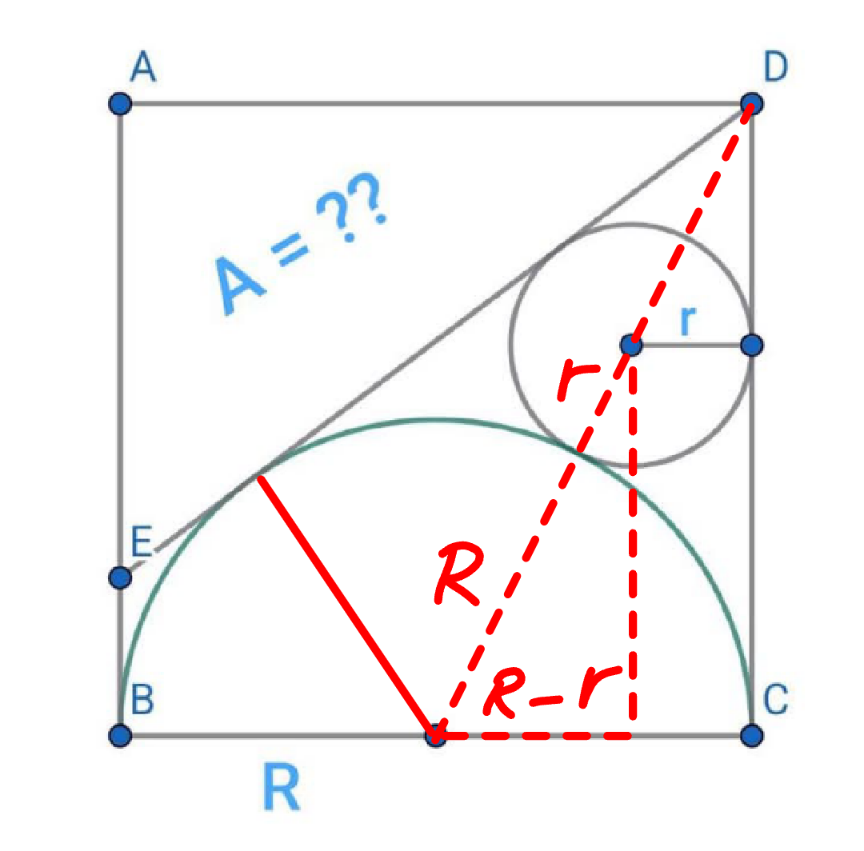
Commented by mr W last updated on 10/Apr/25
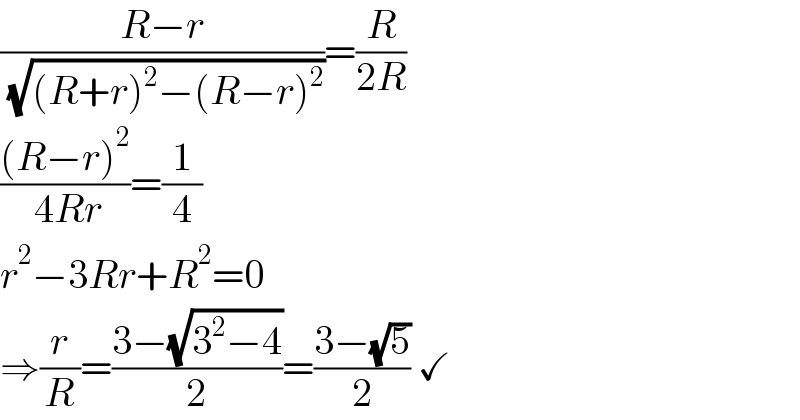
$$\frac{{R}−{r}}{\:\sqrt{\left({R}+{r}\right)^{\mathrm{2}} −\left({R}−{r}\right)^{\mathrm{2}} }}=\frac{{R}}{\mathrm{2}{R}} \\ $$$$\frac{\left({R}−{r}\right)^{\mathrm{2}} }{\:\mathrm{4}{Rr}}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${r}^{\mathrm{2}} −\mathrm{3}{Rr}+{R}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\frac{{r}}{{R}}=\frac{\mathrm{3}−\sqrt{\mathrm{3}^{\mathrm{2}} −\mathrm{4}}}{\mathrm{2}}=\frac{\mathrm{3}−\sqrt{\mathrm{5}}}{\mathrm{2}}\:\checkmark \\ $$
Answered by Spillover last updated on 11/Apr/25
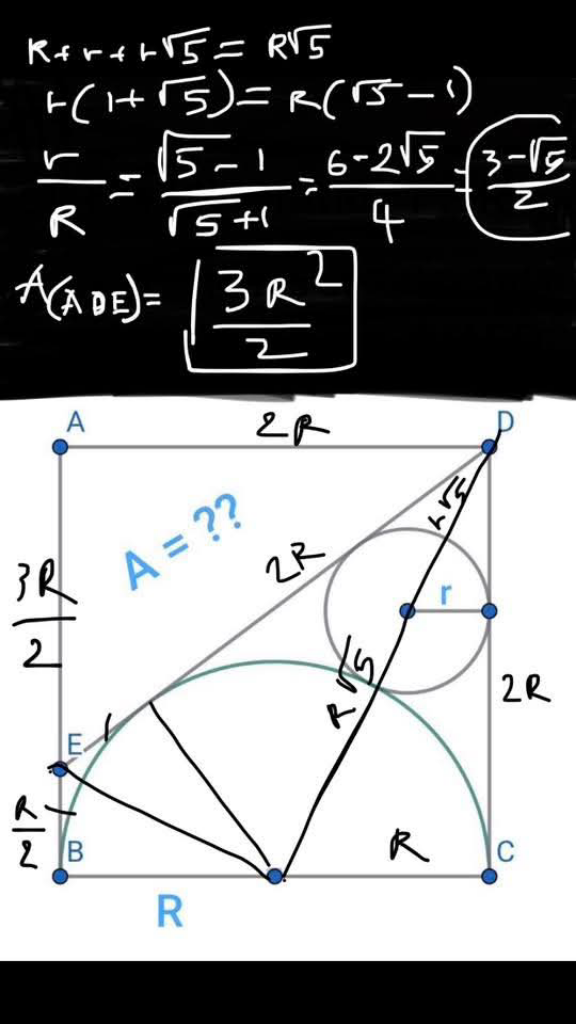
Answered by Spillover last updated on 11/Apr/25