Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

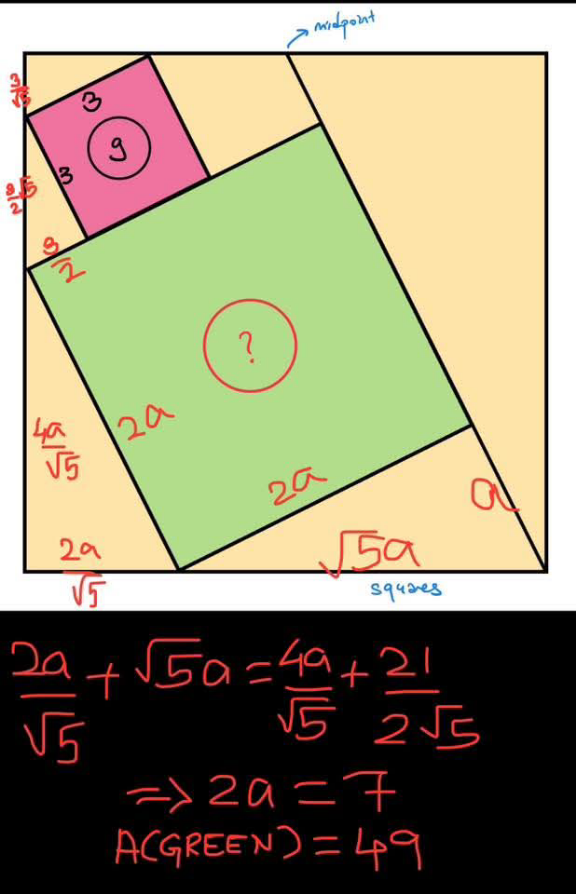
Question Number 218493 by Spillover last updated on 10/Apr/25

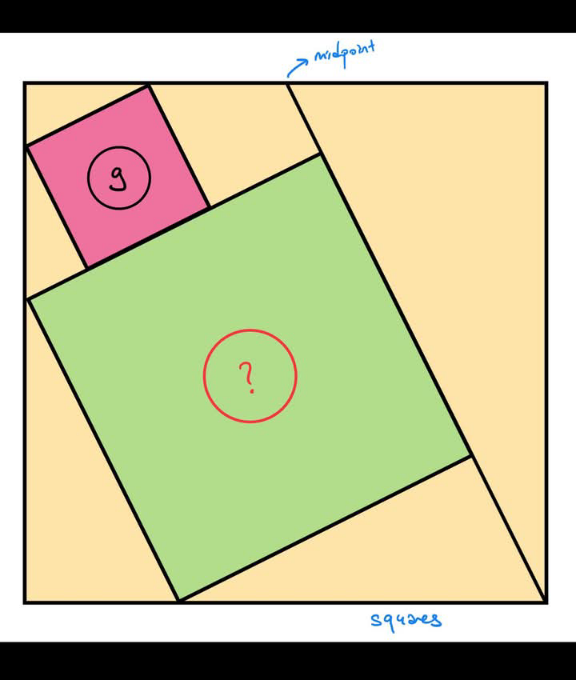
Answered by mr W last updated on 11/Apr/25

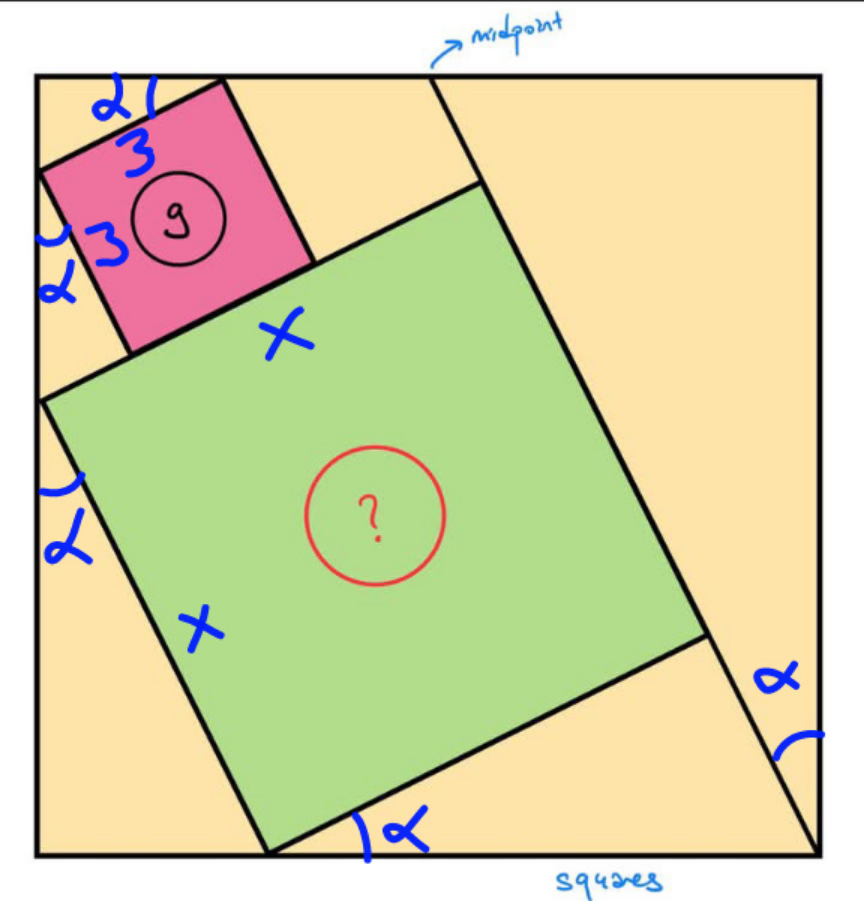
Commented by mr W last updated on 11/Apr/25

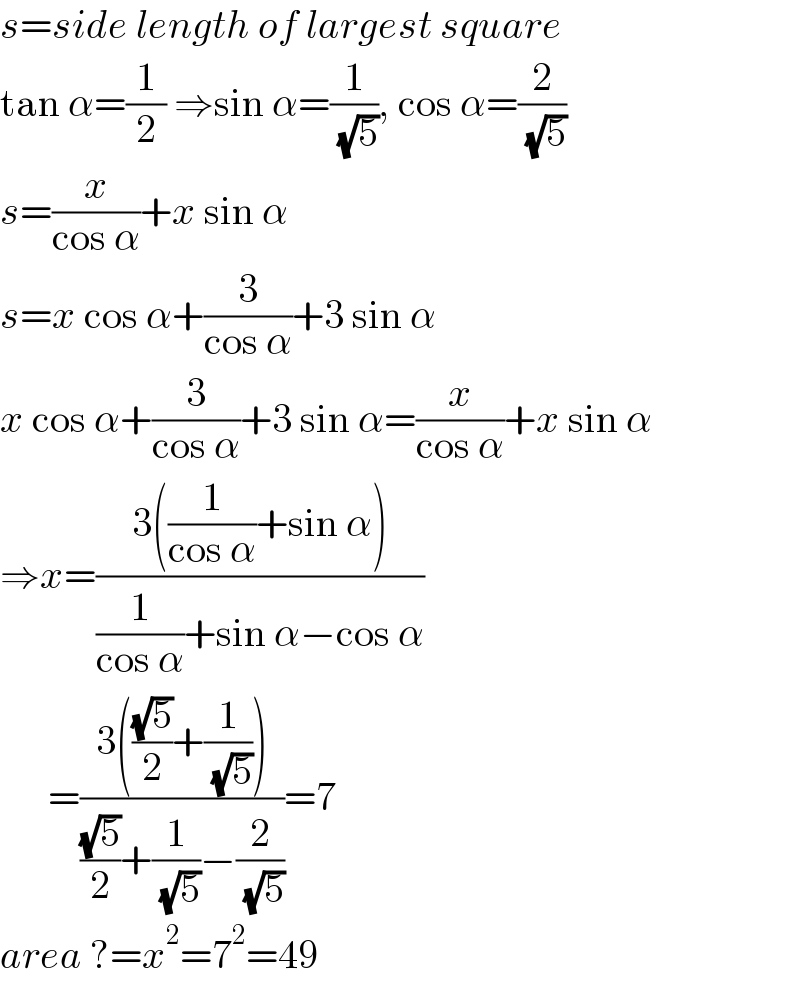
s=side length of largest square tan α=(1/2) ⇒sin α=(1/( (√5))), cos α=(2/( (√5))) s=(x/(cos α))+x sin α s=x cos α+(3/(cos α))+3 sin α x cos α+(3/(cos α))+3 sin α=(x/(cos α))+x sin α ⇒x=((3((1/(cos α))+sin α))/((1/(cos α))+sin α−cos α)) =((3(((√5)/2)+(1/( (√5)))))/(((√5)/2)+(1/( (√5)))−(2/( (√5)))))=7 area ?=x^2 =7^2 =49

$${s}={side}\:{length}\:{of}\:{largest}\:{square} \\ $$$$\mathrm{tan}\:\alpha=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\mathrm{sin}\:\alpha=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}},\:\mathrm{cos}\:\alpha=\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}} \\ $$$${s}=\frac{{x}}{\mathrm{cos}\:\alpha}+{x}\:\mathrm{sin}\:\alpha \\ $$$${s}={x}\:\mathrm{cos}\:\alpha+\frac{\mathrm{3}}{\mathrm{cos}\:\alpha}+\mathrm{3}\:\mathrm{sin}\:\alpha \\ $$$${x}\:\mathrm{cos}\:\alpha+\frac{\mathrm{3}}{\mathrm{cos}\:\alpha}+\mathrm{3}\:\mathrm{sin}\:\alpha=\frac{{x}}{\mathrm{cos}\:\alpha}+{x}\:\mathrm{sin}\:\alpha \\ $$$$\Rightarrow{x}=\frac{\mathrm{3}\left(\frac{\mathrm{1}}{\mathrm{cos}\:\alpha}+\mathrm{sin}\:\alpha\right)}{\frac{\mathrm{1}}{\mathrm{cos}\:\alpha}+\mathrm{sin}\:\alpha−\mathrm{cos}\:\alpha} \\ $$$$\:\:\:\:\:\:=\frac{\mathrm{3}\left(\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\right)}{\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}−\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}}=\mathrm{7} \\ $$$${area}\:?={x}^{\mathrm{2}} =\mathrm{7}^{\mathrm{2}} =\mathrm{49} \\ $$

Commented by Spillover last updated on 11/Apr/25

correct

$${correct} \\ $$

Answered by Spillover last updated on 11/Apr/25

Terms of Service

Privacy Policy

Contact: info@tinkutara.com