
Question Number 218491 by Spillover last updated on 10/Apr/25
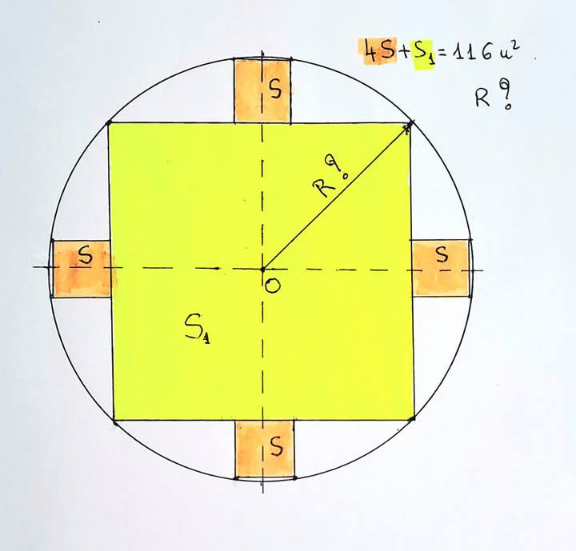
Commented by Nicholas666 last updated on 10/Apr/25

$${R}=\sqrt{\frac{\mathrm{116}}{\pi}} \\ $$
Answered by Nicholas666 last updated on 11/Apr/25
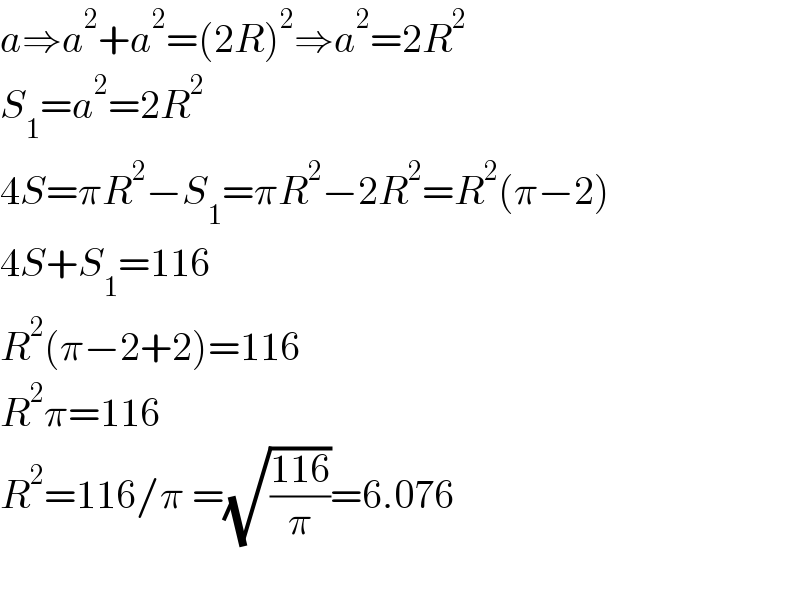
$${a}\Rightarrow{a}^{\mathrm{2}} +{a}^{\mathrm{2}} =\left(\mathrm{2}{R}\right)^{\mathrm{2}} \Rightarrow{a}^{\mathrm{2}} =\mathrm{2}{R}^{\mathrm{2}} \\ $$$${S}_{\mathrm{1}} ={a}^{\mathrm{2}} =\mathrm{2}{R}^{\mathrm{2}} \\ $$$$\mathrm{4}{S}=\pi{R}^{\mathrm{2}} −{S}_{\mathrm{1}} =\pi{R}^{\mathrm{2}} −\mathrm{2}{R}^{\mathrm{2}} ={R}^{\mathrm{2}} \left(\pi−\mathrm{2}\right) \\ $$$$\mathrm{4}{S}+{S}_{\mathrm{1}} =\mathrm{116} \\ $$$${R}^{\mathrm{2}} \left(\pi−\mathrm{2}+\mathrm{2}\right)=\mathrm{116} \\ $$$${R}^{\mathrm{2}} \pi=\mathrm{116} \\ $$$${R}^{\mathrm{2}} =\mathrm{116}/\pi\:=\sqrt{\frac{\mathrm{116}}{\pi}}=\mathrm{6}.\mathrm{076} \\ $$$$ \\ $$
Answered by mr W last updated on 11/Apr/25
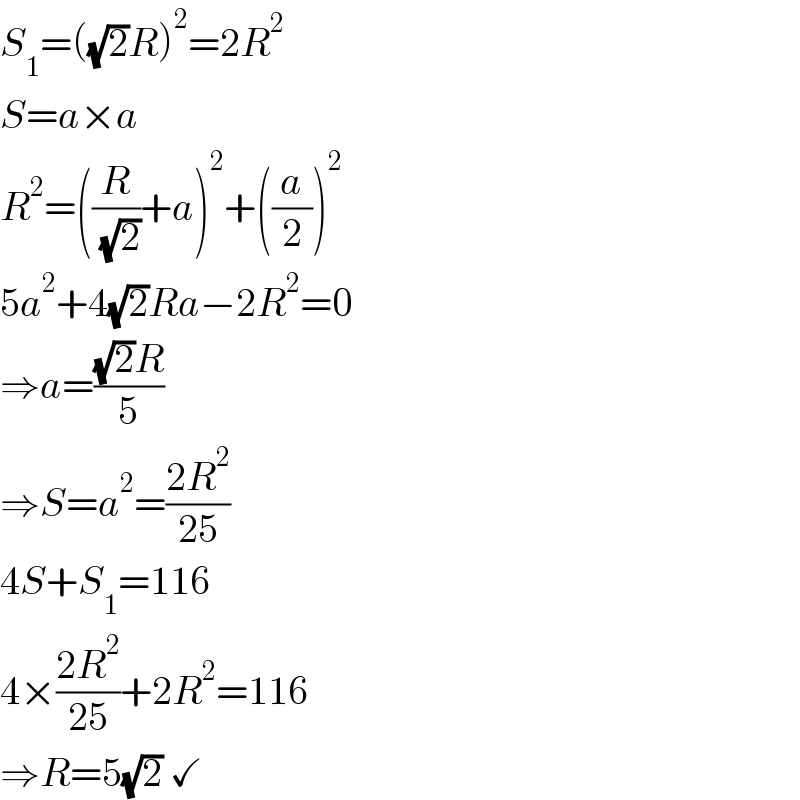
$${S}_{\mathrm{1}} =\left(\sqrt{\mathrm{2}}{R}\right)^{\mathrm{2}} =\mathrm{2}{R}^{\mathrm{2}} \\ $$$${S}={a}×{a} \\ $$$${R}^{\mathrm{2}} =\left(\frac{{R}}{\:\sqrt{\mathrm{2}}}+{a}\right)^{\mathrm{2}} +\left(\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\mathrm{5}{a}^{\mathrm{2}} +\mathrm{4}\sqrt{\mathrm{2}}{Ra}−\mathrm{2}{R}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{a}=\frac{\sqrt{\mathrm{2}}{R}}{\mathrm{5}} \\ $$$$\Rightarrow{S}={a}^{\mathrm{2}} =\frac{\mathrm{2}{R}^{\mathrm{2}} }{\mathrm{25}} \\ $$$$\mathrm{4}{S}+{S}_{\mathrm{1}} =\mathrm{116} \\ $$$$\mathrm{4}×\frac{\mathrm{2}{R}^{\mathrm{2}} }{\mathrm{25}}+\mathrm{2}{R}^{\mathrm{2}} =\mathrm{116} \\ $$$$\Rightarrow{R}=\mathrm{5}\sqrt{\mathrm{2}}\:\checkmark \\ $$
Commented by Spillover last updated on 11/Apr/25

$${correct} \\ $$
Answered by Spillover last updated on 11/Apr/25
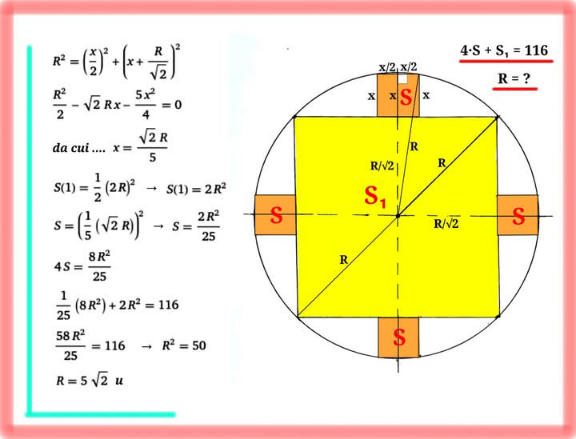
Answered by Spillover last updated on 11/Apr/25
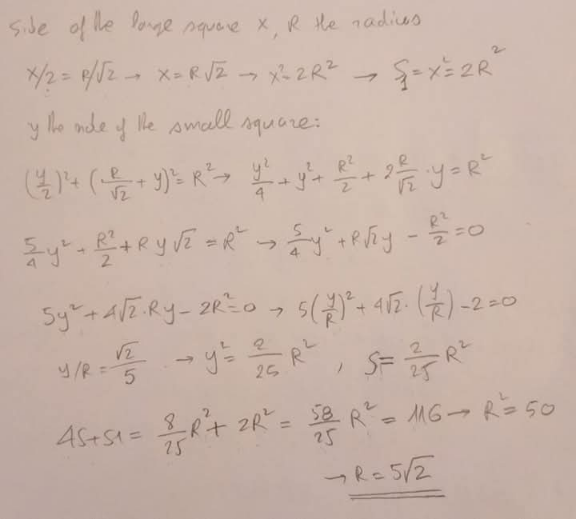
Answered by Spillover last updated on 11/Apr/25

