Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

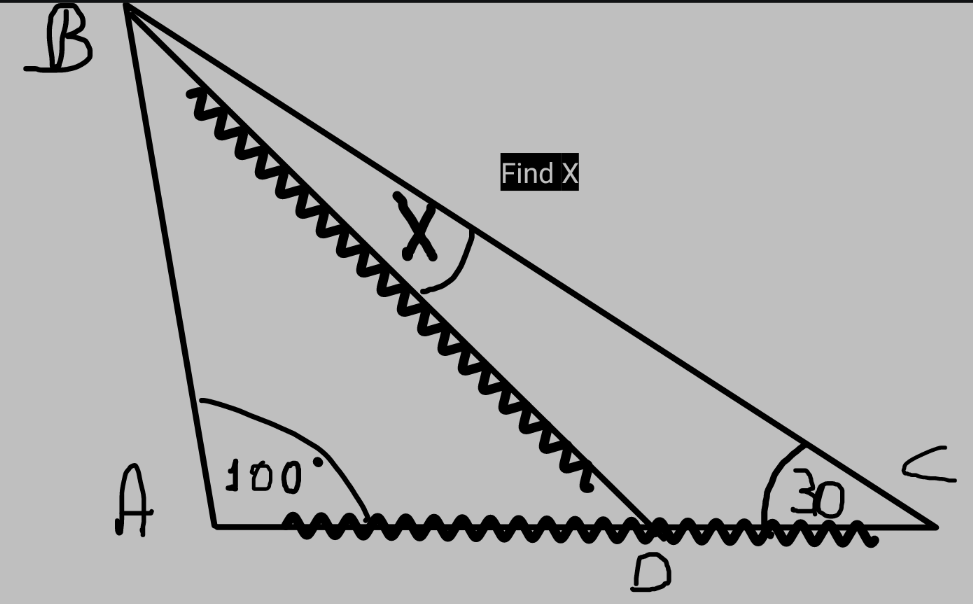
Question Number 218475 by lmcp1203 last updated on 10/Apr/25

Answered by Nicholas666 last updated on 10/Apr/25

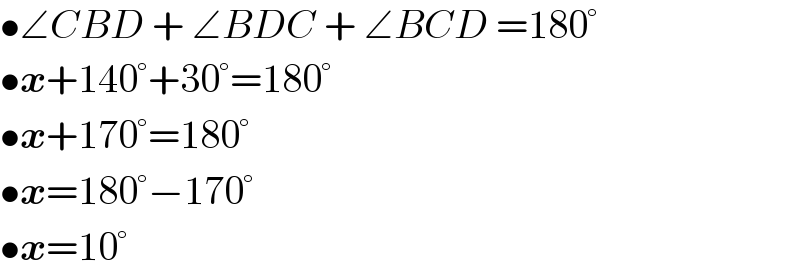
•∠CBD + ∠BDC + ∠BCD =180° •x+140°+30°=180° •x+170°=180° •x=180°−170° •x=10°

$$\bullet\angle{CBD}\:+\:\angle{BDC}\:+\:\angle{BCD}\:=\mathrm{180}° \\ $$$$\bullet\boldsymbol{{x}}+\mathrm{140}°+\mathrm{30}°=\mathrm{180}° \\ $$$$\bullet\boldsymbol{{x}}+\mathrm{170}°=\mathrm{180}° \\ $$$$\bullet\boldsymbol{{x}}=\mathrm{180}°−\mathrm{170}° \\ $$$$\bullet\boldsymbol{{x}}=\mathrm{10}° \\ $$

Commented by mr W last updated on 10/Apr/25

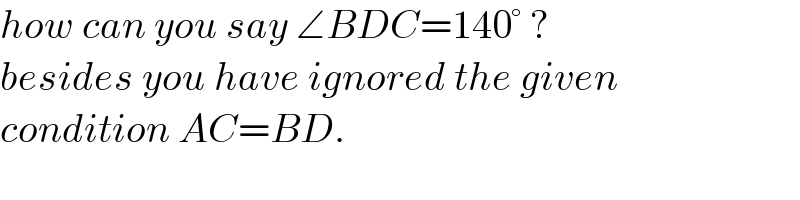
how can you say ∠BDC=140° ? besides you have ignored the given condition AC=BD.

$${how}\:{can}\:{you}\:{say}\:\angle{BDC}=\mathrm{140}°\:? \\ $$$${besides}\:{you}\:{have}\:{ignored}\:{the}\:{given} \\ $$$${condition}\:{AC}={BD}. \\ $$

Commented by Nicholas666 last updated on 10/Apr/25

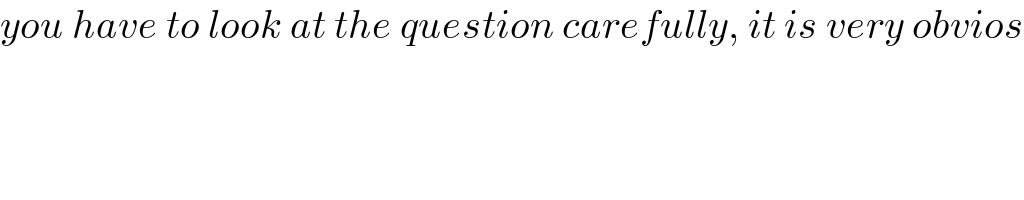
you have to look at the question carefully, it is very obvios

$${you}\:{have}\:{to}\:{look}\:{at}\:{the}\:{question}\:{carefully},\:{it}\:{is}\:{very}\:{obvios} \\ $$

Commented by mr W last updated on 10/Apr/25

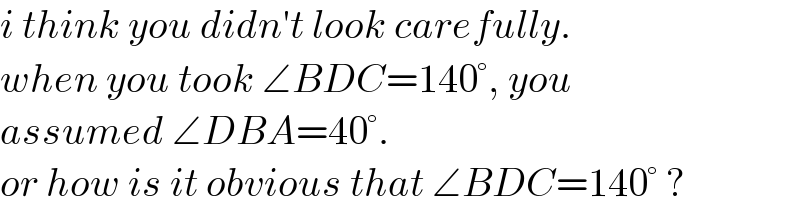
i think you didn′t look carefully. when you took ∠BDC=140°, you assumed ∠DBA=40°. or how is it obvious that ∠BDC=140° ?

$${i}\:{think}\:{you}\:{didn}'{t}\:{look}\:{carefully}. \\ $$$${when}\:{you}\:{took}\:\angle{BDC}=\mathrm{140}°,\:{you} \\ $$$${assumed}\:\angle{DBA}=\mathrm{40}°.\: \\ $$$${or}\:{how}\:{is}\:{it}\:{obvious}\:{that}\:\angle{BDC}=\mathrm{140}°\:? \\ $$

Commented by Nicholas666 last updated on 10/Apr/25

I don′t really like typing at lenght,but okay, I′ll explain to you how I got 10° pay attention to the angle at A is 100° since lines AD and BD have the same sign (jagged lines), this show that triangle ABD is an isosceles triangle AD=BD in an isosceles triangle , the angles opposite the sides of the same lenght are equal. so,angle ABD=ADB calculate the angle ABD and ADB the sum of the angles in a triangle ix 180° in a triangle; ABD:∠BAD+∠ABD+∠ADB=180° 100°+∠ABD+∠ABD=180°(because∠ABD=∠ADB) 2×∠ABD=180°−100° 2×∠ABD=80° ∠ABD=40° so, ∠ADB+∠BDC=180° 40°+∠BDC=180°−40° ∠BDC=140° so,∠CBD+∠BDC+∠BCD x+140°+30°=180° x+170°=180° x=180°−170° x=10° the value of the angle is x=10°

$${I}\:{don}'{t}\:{really}\:{like}\:{typing}\:{at}\:{lenght},{but}\:{okay},\:{I}'{ll}\:{explain}\:{to}\:{you}\:{how}\:{I}\:{got}\:\mathrm{10}° \\ $$$$\:\:{pay}\:{attention}\:{to}\:{the}\:{angle}\:{at}\:{A}\:{is}\:\mathrm{100}° \\ $$$$\:\:{since}\:{lines}\:{AD}\:{and}\:{BD}\:{have}\:{the}\:{same}\:{sign} \\ $$$$\left({jagged}\:{lines}\right),\:{this}\:{show}\:{that}\:{triangle}\:{ABD} \\ $$$${is}\:{an}\:{isosceles}\:{triangle}\:{AD}={BD} \\ $$$$\:\:\:\:{in}\:{an}\:{isosceles}\:{triangle}\:, \\ $$$${the}\:{angles}\:{opposite}\:{the}\:{sides}\:\:{of}\:{the}\:{same}\:{lenght}\:{are}\:{equal}. \\ $$$$\:{so},{angle}\:{ABD}={ADB} \\ $$$$\:\:{calculate}\:{the}\:{angle}\:{ABD}\:{and}\:{ADB} \\ $$$$\:{the}\:{sum}\:{of}\:{the}\:{angles}\:{in}\:{a}\:{triangle}\:{ix}\:\mathrm{180}° \\ $$$${in}\:{a}\:{triangle};\:{ABD}:\angle{BAD}+\angle{ABD}+\angle{ADB}=\mathrm{180}° \\ $$$$\mathrm{100}°+\angle{ABD}+\angle{ABD}=\mathrm{180}°\left({because}\angle{ABD}=\angle{ADB}\right) \\ $$$$\mathrm{2}×\angle{ABD}=\mathrm{180}°−\mathrm{100}° \\ $$$$\mathrm{2}×\angle{ABD}=\mathrm{80}° \\ $$$$\angle{ABD}=\mathrm{40}° \\ $$$${so},\:\angle{ADB}+\angle{BDC}=\mathrm{180}° \\ $$$$\mathrm{40}°+\angle{BDC}=\mathrm{180}°−\mathrm{40}° \\ $$$$\angle{BDC}=\mathrm{140}° \\ $$$${so},\angle{CBD}+\angle{BDC}+\angle{BCD} \\ $$$${x}+\mathrm{140}°+\mathrm{30}°=\mathrm{180}° \\ $$$${x}+\mathrm{170}°=\mathrm{180}° \\ $$$${x}=\mathrm{180}°−\mathrm{170}° \\ $$$${x}=\mathrm{10}° \\ $$$${the}\:{value}\:{of}\:{the}\:{angle}\:{is}\:\boldsymbol{{x}}=\mathrm{10}° \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by mr W last updated on 11/Apr/25

sorry, not AD and BD have the same sign, but AC and BD have the same sign. that means AC=BD, not AD=BD as you said. besides, even if you′re right with AD=BD, then you should not get ∠ABD=∠ADB, but get ∠ABD=∠DAB=100°. that′s definitively not right. please recheck sir.

$${sorry},\:{not}\:{AD}\:{and}\:{BD}\:{have}\:{the} \\ $$$${same}\:{sign},\:{but}\:{AC}\:{and}\:{BD}\:{have} \\ $$$${the}\:{same}\:{sign}.\:{that}\:{means}\:{AC}={BD}, \\ $$$${not}\:{AD}={BD}\:{as}\:{you}\:{said}.\:\:{besides}, \\ $$$${even}\:{if}\:{you}'{re}\:{right}\:{with}\:{AD}={BD},\: \\ $$$${then}\:{you}\:{should}\:{not}\:{get}\: \\ $$$$\angle{ABD}=\angle{ADB},\:{but}\:{get}\: \\ $$$$\angle{ABD}=\angle{DAB}=\mathrm{100}°.\:{that}'{s}\: \\ $$$${definitively}\:{not}\:{right}. \\ $$$${please}\:{recheck}\:{sir}. \\ $$

Answered by lmcp1203 last updated on 10/Apr/25

thanks

$${thanks} \\ $$

Answered by vnm last updated on 10/Apr/25

AC=BD=a ((AB)/(sin 30°))=((AC)/(sin∠ABC)) AB=(a/(2sin 50°)) E is the base of the perpendicular drawn from B to the line AC BE=ABsin 80°=((asin 80°)/(2sin 50°))=BDsin∠BDA=asin∠BDA sin∠BDA=((sin 80°)/(2sin 50°))=sin ∠BDC ∠BDC=180°−sin^(−1) (sin∠BDA) x=∠DBC=180°−(∠DCB+∠BDC)= 180°−(30°+180°−sin^(−1) (((sin 80°)/(2sin 50°))))= sin^(−1) (((sin 80°)/(2sin 50°)))−30° ((sin 80°)/(2sin 50°))=((2sin 40°cos 40°)/(2sin(90°−40°)))=sin 40° x=sin^(−1) (sin 40°)−30°=10°

$$ \\ $$$${AC}={BD}={a} \\ $$$$\frac{{AB}}{\mathrm{sin}\:\mathrm{30}°}=\frac{{AC}}{\mathrm{sin}\angle{ABC}} \\ $$$${AB}=\frac{{a}}{\mathrm{2sin}\:\mathrm{50}°} \\ $$$$\mathrm{E}\:\mathrm{is}\:\mathrm{the}\:\mathrm{base}\:\mathrm{of}\:\mathrm{the}\:\mathrm{perpendicular}\: \\ $$$$\mathrm{drawn}\:\mathrm{from}\:\mathrm{B}\:\mathrm{to}\:\mathrm{the}\:\mathrm{line}\:\mathrm{AC} \\ $$$${BE}={AB}\mathrm{sin}\:\mathrm{80}°=\frac{{a}\mathrm{sin}\:\mathrm{80}°}{\mathrm{2sin}\:\mathrm{50}°}={BD}\mathrm{sin}\angle{BDA}={a}\mathrm{sin}\angle{BDA} \\ $$$$\mathrm{sin}\angle{BDA}=\frac{\mathrm{sin}\:\mathrm{80}°}{\mathrm{2sin}\:\mathrm{50}°}=\mathrm{sin}\:\angle{BDC} \\ $$$$\angle{BDC}=\mathrm{180}°−\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{sin}\angle{BDA}\right) \\ $$$${x}=\angle{DBC}=\mathrm{180}°−\left(\angle{DCB}+\angle{BDC}\right)= \\ $$$$\mathrm{180}°−\left(\mathrm{30}°+\mathrm{180}°−\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{sin}\:\mathrm{80}°}{\mathrm{2sin}\:\mathrm{50}°}\right)\right)= \\ $$$$\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{sin}\:\mathrm{80}°}{\mathrm{2sin}\:\mathrm{50}°}\right)−\mathrm{30}° \\ $$$$\frac{\mathrm{sin}\:\mathrm{80}°}{\mathrm{2sin}\:\mathrm{50}°}=\frac{\mathrm{2sin}\:\mathrm{40}°\mathrm{cos}\:\mathrm{40}°}{\mathrm{2sin}\left(\mathrm{90}°−\mathrm{40}°\right)}=\mathrm{sin}\:\mathrm{40}° \\ $$$${x}=\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{sin}\:\mathrm{40}°\right)−\mathrm{30}°=\mathrm{10}° \\ $$

Commented by mr W last updated on 11/Apr/25

��

Answered by lmcp1203 last updated on 10/Apr/25

thank[you

$${thank}\left[{you}\:\right. \\ $$

Answered by Spillover last updated on 11/Apr/25

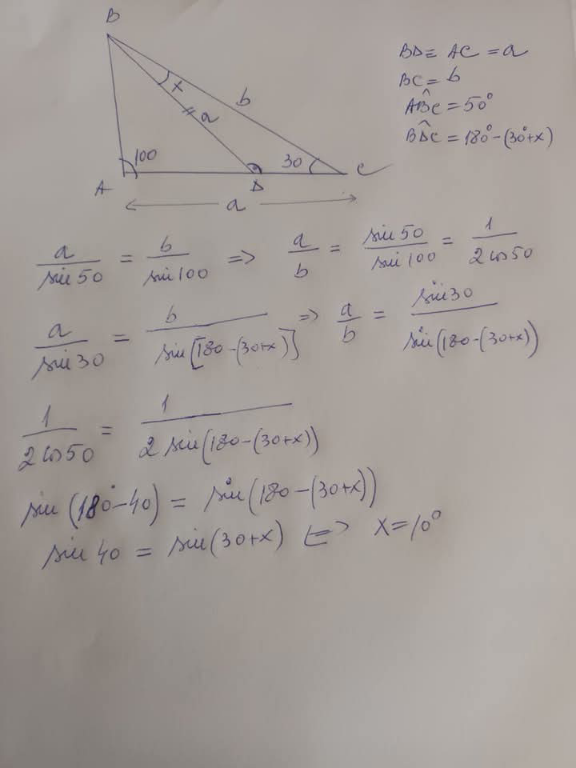
Commented by lmcp1203 last updated on 16/Apr/25

thank you

$${thank}\:{you} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com