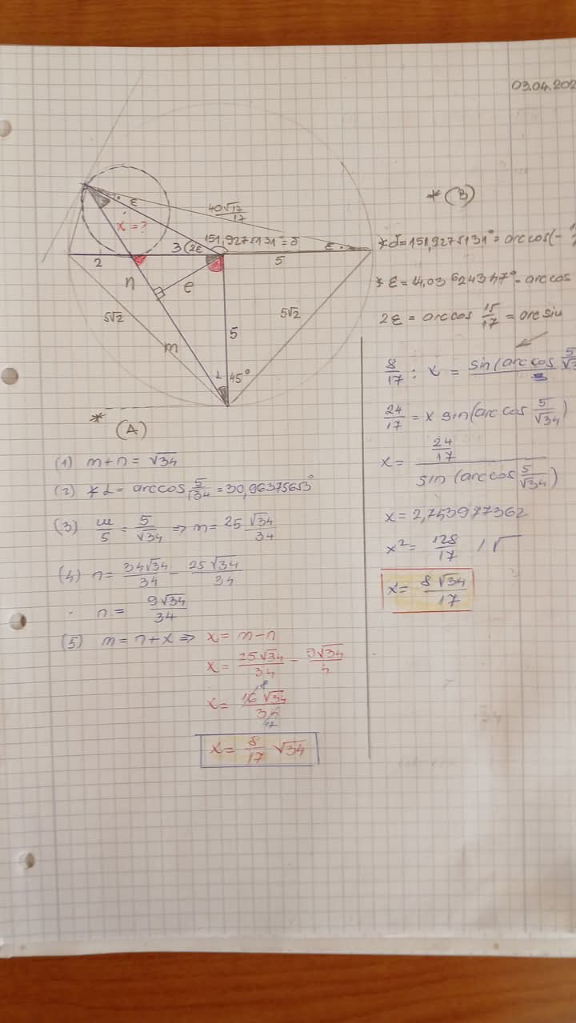
Question Number 218456 by Spillover last updated on 10/Apr/25
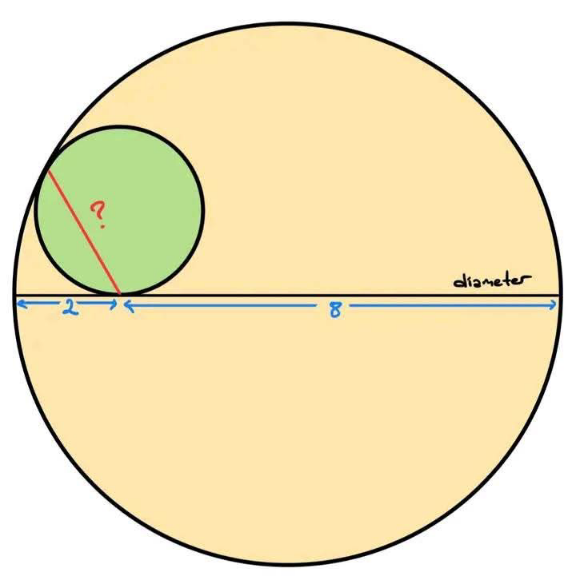
Answered by vnm last updated on 10/Apr/25
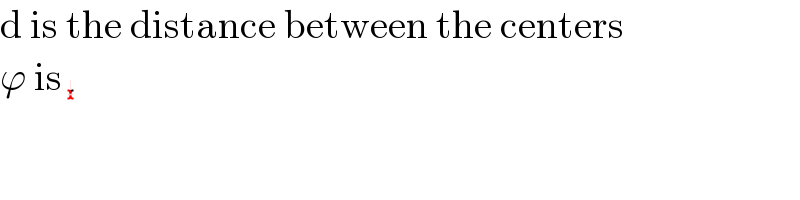
$$\mathrm{d}\:\mathrm{is}\:\mathrm{the}\:\mathrm{distance}\:\mathrm{between}\:\mathrm{the}\:\mathrm{centers} \\ $$$$\varphi\:\mathrm{is}\:\mathscr{L}\cancel{\underbrace{ }} \\ $$
Commented by Spillover last updated on 10/Apr/25

$${correct} \\ $$
Answered by mr W last updated on 10/Apr/25
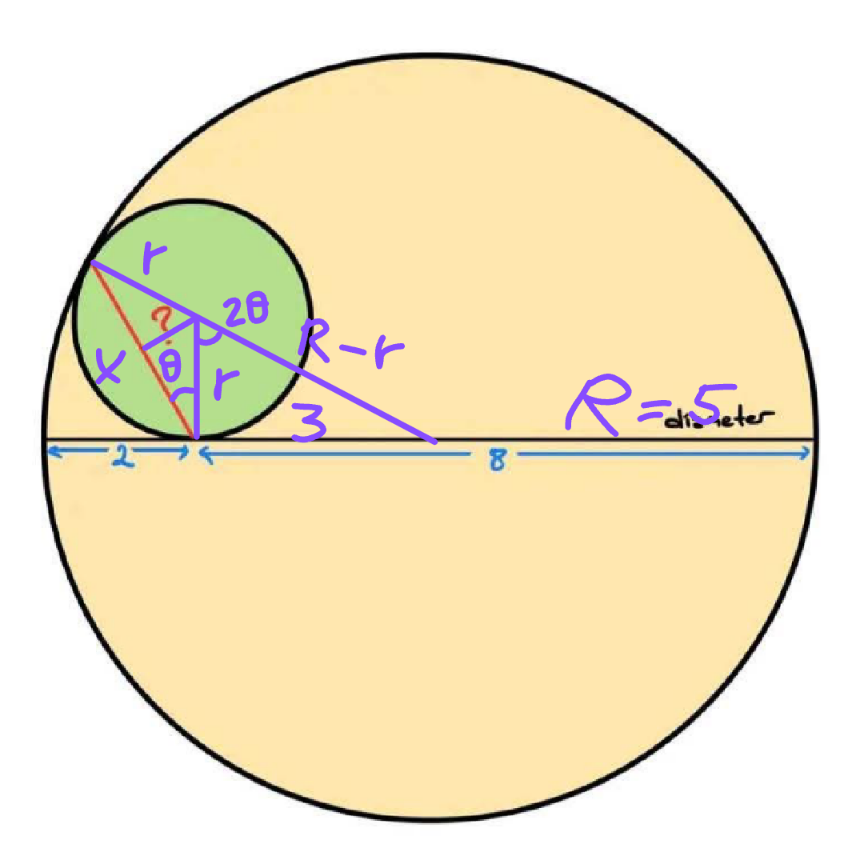
Commented by mr W last updated on 10/Apr/25
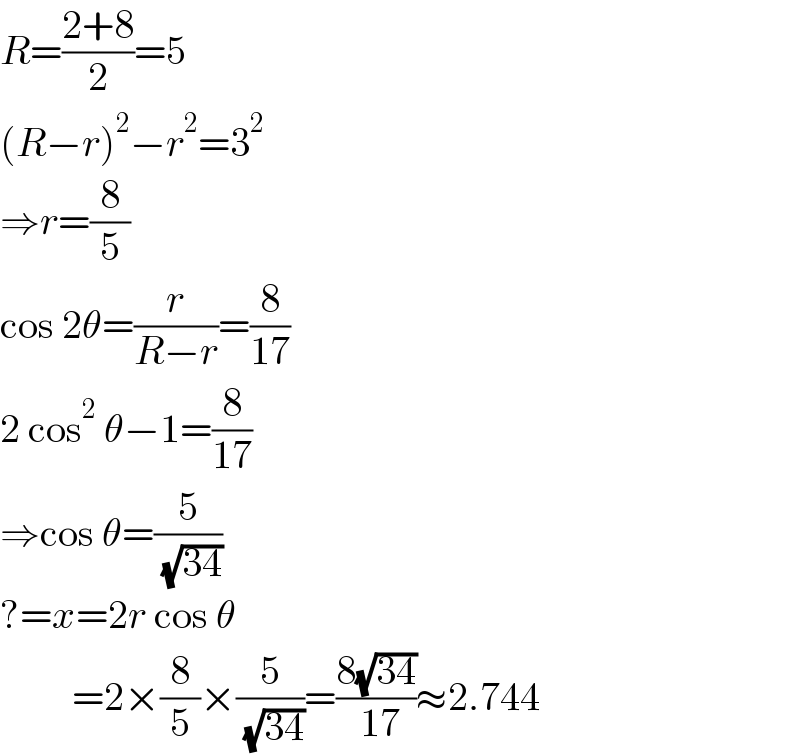
$${R}=\frac{\mathrm{2}+\mathrm{8}}{\mathrm{2}}=\mathrm{5} \\ $$$$\left({R}−{r}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} =\mathrm{3}^{\mathrm{2}} \\ $$$$\Rightarrow{r}=\frac{\mathrm{8}}{\mathrm{5}} \\ $$$$\mathrm{cos}\:\mathrm{2}\theta=\frac{{r}}{{R}−{r}}=\frac{\mathrm{8}}{\mathrm{17}} \\ $$$$\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:\theta−\mathrm{1}=\frac{\mathrm{8}}{\mathrm{17}} \\ $$$$\Rightarrow\mathrm{cos}\:\theta=\frac{\mathrm{5}}{\:\sqrt{\mathrm{34}}} \\ $$$$?={x}=\mathrm{2}{r}\:\mathrm{cos}\:\theta \\ $$$$\:\:\:\:\:\:\:\:\:=\mathrm{2}×\frac{\mathrm{8}}{\mathrm{5}}×\frac{\mathrm{5}}{\:\sqrt{\mathrm{34}}}=\frac{\mathrm{8}\sqrt{\mathrm{34}}}{\:\mathrm{17}}\approx\mathrm{2}.\mathrm{744} \\ $$
Answered by Spillover last updated on 10/Apr/25
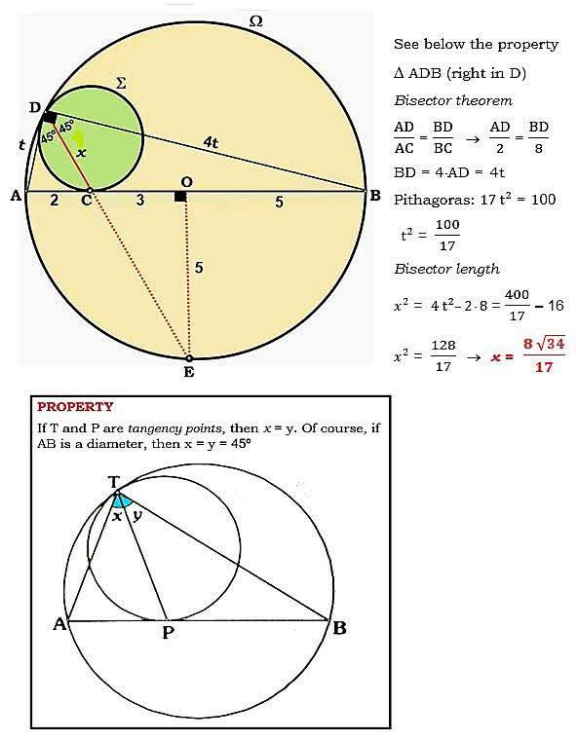
Answered by Spillover last updated on 10/Apr/25
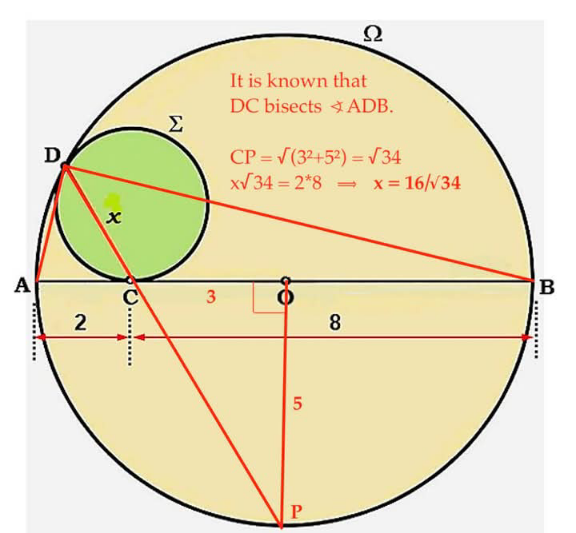
Answered by Spillover last updated on 10/Apr/25