Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

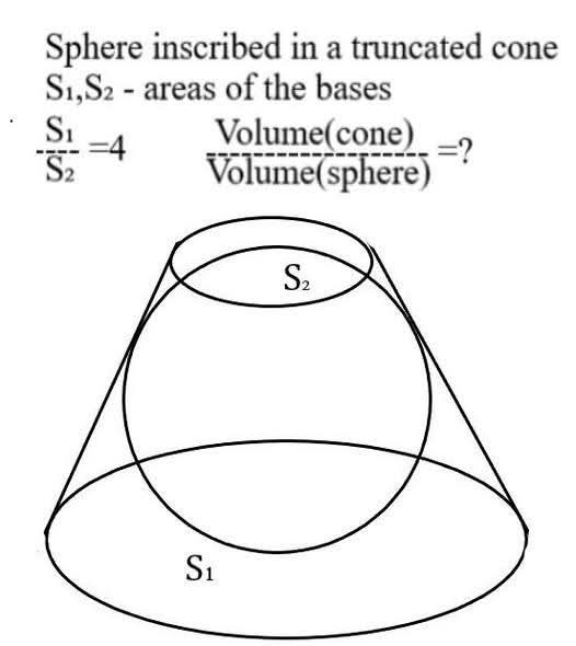
Question Number 218411 by Spillover last updated on 09/Apr/25

Answered by mr W last updated on 09/Apr/25

Commented by mr W last updated on 09/Apr/25

S_1 =πr_1 ^2 S_2 =πr_2 ^2 (S_1 /S_2 )=((r_1 /r_2 ))^2 =4 ⇒(r_1 /r_2 )=2 V_1 =((S_1 h_1 )/3)=((πr_1 ^2 h_1 )/3) V_2 =((S_2 h_2 )/3)=((πr_2 ^2 h_2 )/3) V_C =V_1 −V_2 =volume of cone V_S =((4πR^3 )/3)=volume of sphere h_1 =h_2 +2R (h_1 /h_2 )=(r_1 /r_2 )=2 ((h_2 +2R)/h_2 )=2 ⇒(R/h_2 )=(1/2) ⇒h_2 =2R (r_2 /R)=((√(h_2 ^2 +r_2 ^2 ))/(h_2 +R)) (r_2 /R)=((√(4R^2 +r_2 ^2 ))/(2R+R)) 2r_2 ^2 =R^2 ⇒(r_2 ^2 /R^2 )=(1/2) (V_C /V_S )=((r_1 ^2 h_1 −r_2 ^2 h_2 )/(4R^3 )) =((4r_2 ^2 ×2h_2 −r_2 ^2 h_2 )/(4R^3 )) =((7r_2 ^2 ×2R)/(4R^3 ))=((7r_2 ^2 )/(2R^2 ))=(7/4) ✓

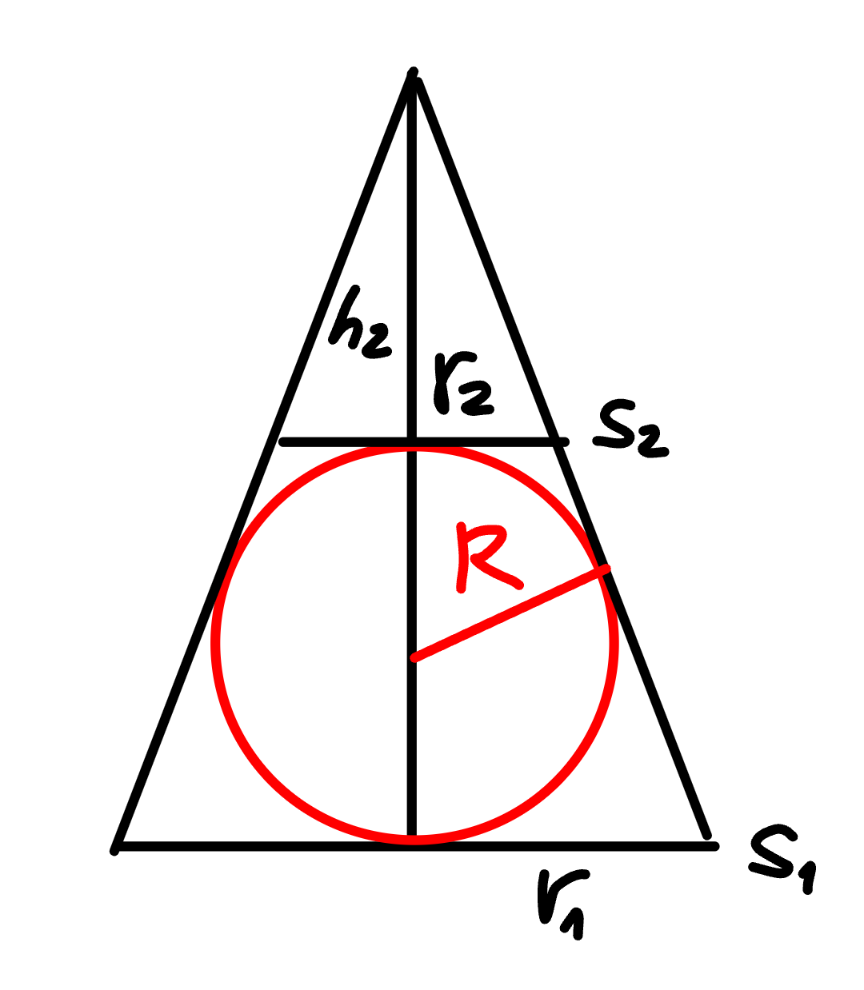
$${S}_{\mathrm{1}} =\pi{r}_{\mathrm{1}} ^{\mathrm{2}} \\ $$$${S}_{\mathrm{2}} =\pi{r}_{\mathrm{2}} ^{\mathrm{2}} \\ $$$$\frac{{S}_{\mathrm{1}} }{{S}_{\mathrm{2}} }=\left(\frac{{r}_{\mathrm{1}} }{{r}_{\mathrm{2}} }\right)^{\mathrm{2}} =\mathrm{4}\:\Rightarrow\frac{{r}_{\mathrm{1}} }{{r}_{\mathrm{2}} }=\mathrm{2} \\ $$$${V}_{\mathrm{1}} =\frac{{S}_{\mathrm{1}} {h}_{\mathrm{1}} }{\mathrm{3}}=\frac{\pi{r}_{\mathrm{1}} ^{\mathrm{2}} {h}_{\mathrm{1}} }{\mathrm{3}} \\ $$$${V}_{\mathrm{2}} =\frac{{S}_{\mathrm{2}} {h}_{\mathrm{2}} }{\mathrm{3}}=\frac{\pi{r}_{\mathrm{2}} ^{\mathrm{2}} {h}_{\mathrm{2}} }{\mathrm{3}} \\ $$$${V}_{{C}} ={V}_{\mathrm{1}} −{V}_{\mathrm{2}} ={volume}\:{of}\:{cone} \\ $$$${V}_{{S}} =\frac{\mathrm{4}\pi{R}^{\mathrm{3}} }{\mathrm{3}}={volume}\:{of}\:{sphere} \\ $$$${h}_{\mathrm{1}} ={h}_{\mathrm{2}} +\mathrm{2}{R} \\ $$$$\frac{{h}_{\mathrm{1}} }{{h}_{\mathrm{2}} }=\frac{{r}_{\mathrm{1}} }{{r}_{\mathrm{2}} }=\mathrm{2} \\ $$$$\frac{{h}_{\mathrm{2}} +\mathrm{2}{R}}{{h}_{\mathrm{2}} }=\mathrm{2}\:\Rightarrow\frac{{R}}{{h}_{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow{h}_{\mathrm{2}} =\mathrm{2}{R} \\ $$$$\frac{{r}_{\mathrm{2}} }{{R}}=\frac{\sqrt{{h}_{\mathrm{2}} ^{\mathrm{2}} +{r}_{\mathrm{2}} ^{\mathrm{2}} }}{{h}_{\mathrm{2}} +{R}} \\ $$$$\frac{{r}_{\mathrm{2}} }{{R}}=\frac{\sqrt{\mathrm{4}{R}^{\mathrm{2}} +{r}_{\mathrm{2}} ^{\mathrm{2}} }}{\mathrm{2}{R}+{R}} \\ $$$$\mathrm{2}{r}_{\mathrm{2}} ^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$$\Rightarrow\frac{{r}_{\mathrm{2}} ^{\mathrm{2}} }{{R}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{{V}_{{C}} }{{V}_{{S}} }=\frac{{r}_{\mathrm{1}} ^{\mathrm{2}} {h}_{\mathrm{1}} −{r}_{\mathrm{2}} ^{\mathrm{2}} {h}_{\mathrm{2}} }{\mathrm{4}{R}^{\mathrm{3}} } \\ $$$$\:\:\:\:\:=\frac{\mathrm{4}{r}_{\mathrm{2}} ^{\mathrm{2}} ×\mathrm{2}{h}_{\mathrm{2}} −{r}_{\mathrm{2}} ^{\mathrm{2}} {h}_{\mathrm{2}} }{\mathrm{4}{R}^{\mathrm{3}} } \\ $$$$\:\:\:\:\:=\frac{\mathrm{7}{r}_{\mathrm{2}} ^{\mathrm{2}} ×\mathrm{2}{R}}{\mathrm{4}{R}^{\mathrm{3}} }=\frac{\mathrm{7}{r}_{\mathrm{2}} ^{\mathrm{2}} }{\mathrm{2}{R}^{\mathrm{2}} }=\frac{\mathrm{7}}{\mathrm{4}}\:\checkmark \\ $$

Commented by Spillover last updated on 09/Apr/25

thank you

$${thank}\:{you} \\ $$

Answered by Nicholas666 last updated on 09/Apr/25

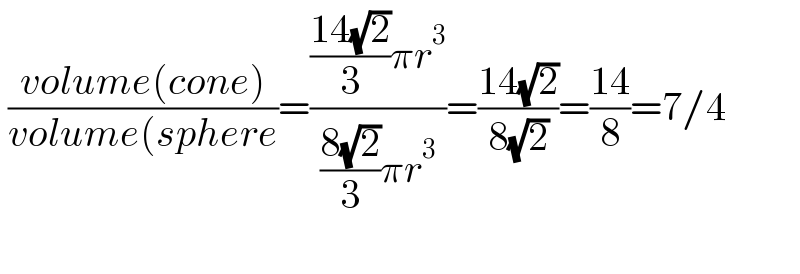
((volume(cone))/(volume(sphere))=((((14(√2))/3)πr^3 )/(((8(√2))/3)πr^3 ))=((14(√2))/(8(√2)))=((14)/8)=7/4

$$\:\frac{{volume}\left({cone}\right)}{{volume}\left({sphere}\right.}=\frac{\frac{\mathrm{14}\sqrt{\mathrm{2}}}{\mathrm{3}}\pi{r}^{\mathrm{3}} }{\frac{\mathrm{8}\sqrt{\mathrm{2}}}{\mathrm{3}}\pi{r}^{\mathrm{3}} }=\frac{\mathrm{14}\sqrt{\mathrm{2}}}{\mathrm{8}\sqrt{\mathrm{2}}}=\frac{\mathrm{14}}{\mathrm{8}}=\mathrm{7}/\mathrm{4} \\ $$$$ \\ $$

Commented by mr W last updated on 11/Apr/25

it makes little sense, when you just post a result without showing how to get it. people want to know the path, not only the final answer.

$${it}\:{makes}\:{little}\:{sense},\:{when}\:{you}\:{just} \\ $$$${post}\:{a}\:{result}\:{without}\:{showing}\:{how} \\ $$$${to}\:{get}\:{it}.\:{people}\:{want}\:{to}\:{know}\:{the} \\ $$$${path},\:{not}\:{only}\:{the}\:{final}\:{answer}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com