Question Number 218410 by Spillover last updated on 09/Apr/25
Answered by Nicholas666 last updated on 09/Apr/25

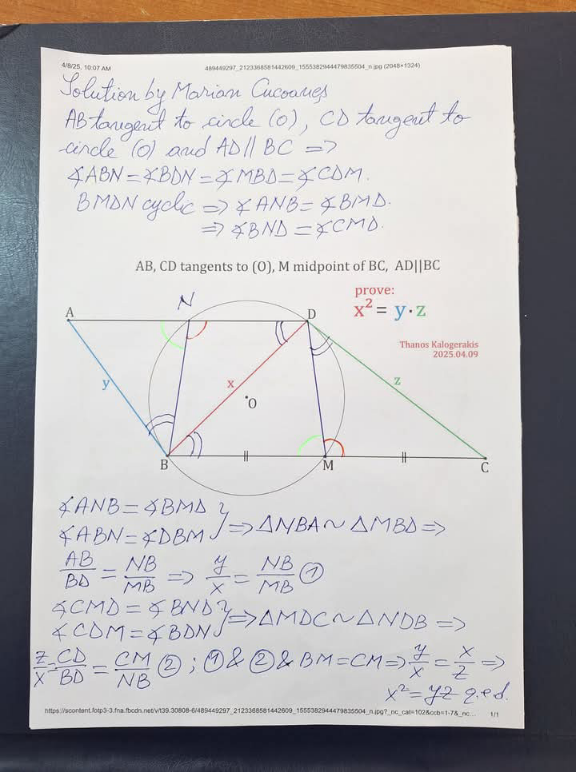
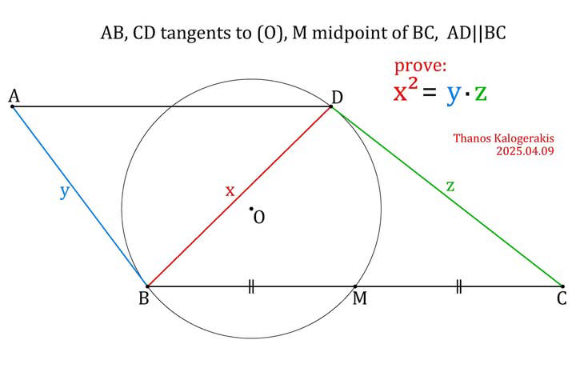
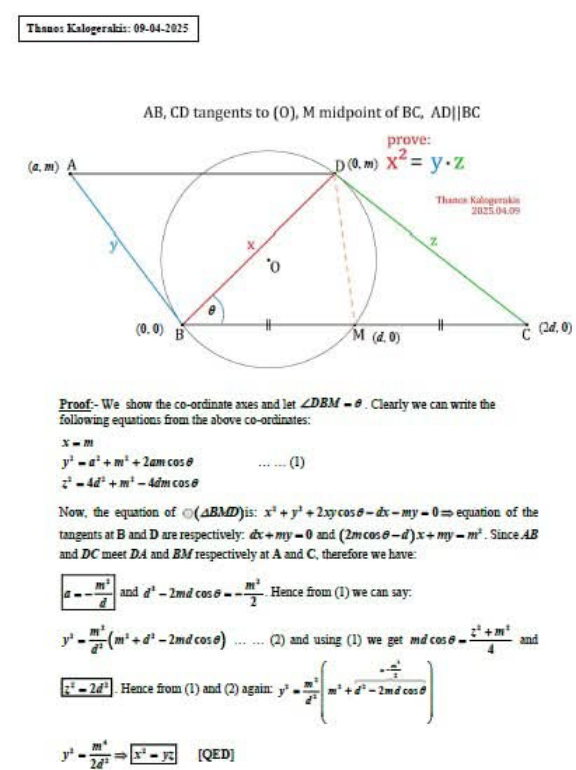
$$\:{given};{AB},{CD}\:{tangents}\:{to}\:{circle}\:{O}: \\ $$$${M}\:{midpoint}\:{of}\:{BC};\:{AD}\mid\mid{BC};\:{BD}={x},{AB}={y},{CD}={z} \\ $$$${prove}\:{x}^{\mathrm{2}} ={y}.{z} \\ $$$${solution} \\ $$$$\ast{AD}\mid\mid{BC} \angle{ABD}=\angle{DBC}\:\:\left({alternate}\:{interior}\:{angles}\right)\: \\ $$$$\ast\angle{ABD}=\angle{BDC}\:\:\left({angle}\:{between}\:{tangent}\:{and}\:{chord}\right)\: \\ $$$$\ast{ABD}\sim\bigtriangleup{BDC}\:\left({AA}:\:\angle{ABD}=\angle{DBC},\:\angle{ABD}=\angle{BDC}\right)\: \\ $$$$\ast{ratio}\:{of}\:{corresponding}\:{sides};\:{AB}/{BD}={BD}/{CD}\: \\ $$$$\ast\:\:{y}/{x}={x}/{z}={y}.{z}={x}.{x}={y}.{z}={x}^{\mathrm{2}} \\ $$$$\ast{cross}−{multiply}\::\:{x}^{\mathrm{2}} ={y}.{z} \\ $$$$ \\ $$$${q}.{e}.{d} \\ $$$$ \\ $$
Answered by Spillover last updated on 10/Apr/25
Answered by Spillover last updated on 10/Apr/25