
Question Number 218385 by Spillover last updated on 08/Apr/25
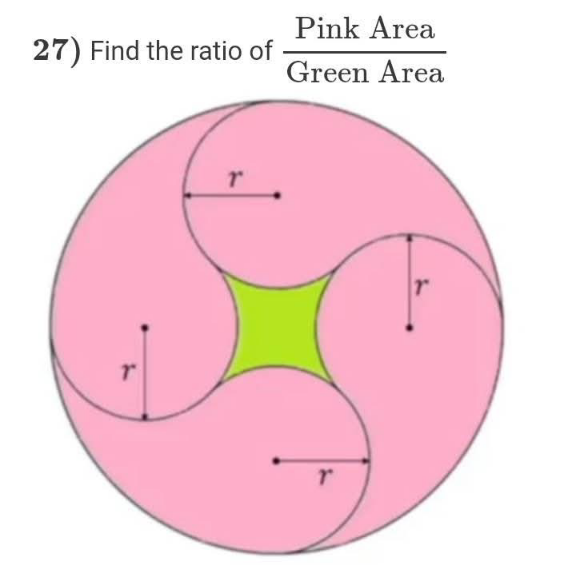
Answered by Nicholas666 last updated on 09/Apr/25
$${ratio}=\frac{\mathrm{3}.\mathrm{2}}{\mathrm{2}.\mathrm{5}}=\mathrm{6}/\mathrm{10}=\mathrm{3}/\mathrm{5}=\mathrm{0}.\mathrm{6} \\ $$
Answered by Spillover last updated on 09/Apr/25

Answered by mr W last updated on 10/Apr/25
![R=radius of big circle 2R=r+(√2)×2r+r ⇒R=(1+(√2))r A_(green) =(2r)^2 −4×((πr^2 )/4)=(4−π)r^2 A_(pink) =πR^2 −A_(green) =(1+(√2))^2 πr^2 −(4−π)r^2 =[(4+2(√2))π−4]r^2 ((pink)/(green))=(((4+2(√2))π−4)/(4−π))≈20.331](Q218442.png)
$${R}={radius}\:{of}\:{big}\:{circle} \\ $$$$\mathrm{2}{R}={r}+\sqrt{\mathrm{2}}×\mathrm{2}{r}+{r} \\ $$$$\Rightarrow{R}=\left(\mathrm{1}+\sqrt{\mathrm{2}}\right){r} \\ $$$${A}_{{green}} =\left(\mathrm{2}{r}\right)^{\mathrm{2}} −\mathrm{4}×\frac{\pi{r}^{\mathrm{2}} }{\mathrm{4}}=\left(\mathrm{4}−\pi\right){r}^{\mathrm{2}} \\ $$$${A}_{{pink}} =\pi{R}^{\mathrm{2}} −{A}_{{green}} =\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \pi{r}^{\mathrm{2}} −\left(\mathrm{4}−\pi\right){r}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\left[\left(\mathrm{4}+\mathrm{2}\sqrt{\mathrm{2}}\right)\pi−\mathrm{4}\right]{r}^{\mathrm{2}} \\ $$$$\frac{{pink}}{{green}}=\frac{\left(\mathrm{4}+\mathrm{2}\sqrt{\mathrm{2}}\right)\pi−\mathrm{4}}{\mathrm{4}−\pi}\approx\mathrm{20}.\mathrm{331} \\ $$
Commented by Spillover last updated on 10/Apr/25
$${thank}\:{you} \\ $$
