
Question Number 218366 by Mingma last updated on 08/Apr/25

Commented by Mingma last updated on 08/Apr/25
Find the dimensions
Commented by zetamaths last updated on 08/Apr/25
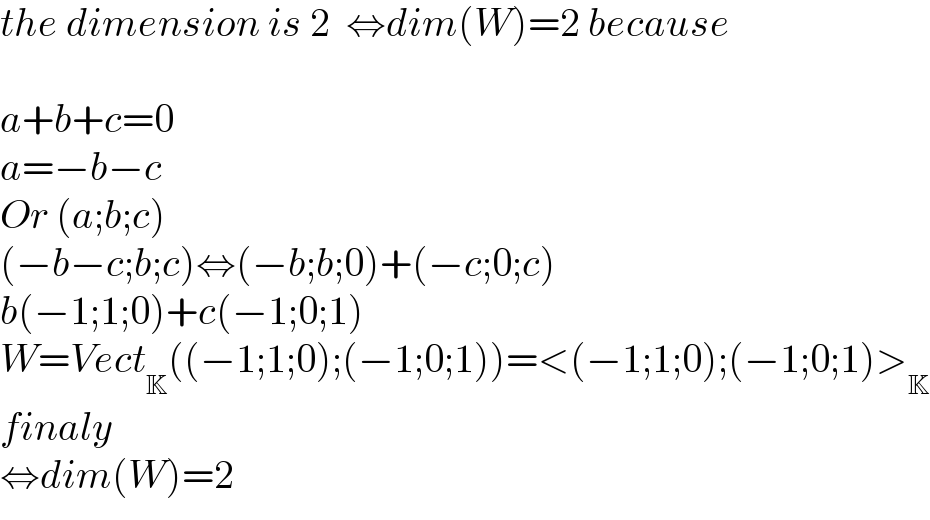
$${the}\:{dimension}\:{is}\:\mathrm{2}\:\:\Leftrightarrow{dim}\left({W}\right)=\mathrm{2}\:{because} \\ $$$$ \\ $$$${a}+{b}+{c}=\mathrm{0} \\ $$$${a}=−{b}−{c}\:\: \\ $$$${Or}\:\left({a};{b};{c}\right) \\ $$$$\left(−{b}−{c};{b};{c}\right)\Leftrightarrow\left(−{b};{b};\mathrm{0}\right)+\left(−{c};\mathrm{0};{c}\right) \\ $$$${b}\left(−\mathrm{1};\mathrm{1};\mathrm{0}\right)+{c}\left(−\mathrm{1};\mathrm{0};\mathrm{1}\right) \\ $$$${W}={Vect}_{\mathbb{K}} \left(\left(−\mathrm{1};\mathrm{1};\mathrm{0}\right);\left(−\mathrm{1};\mathrm{0};\mathrm{1}\right)\right)=<\left(−\mathrm{1};\mathrm{1};\mathrm{0}\right);\left(−\mathrm{1};\mathrm{0};\mathrm{1}\right)>_{\mathbb{K}} \\ $$$${finaly} \\ $$$$\Leftrightarrow{dim}\left({W}\right)=\mathrm{2} \\ $$
