
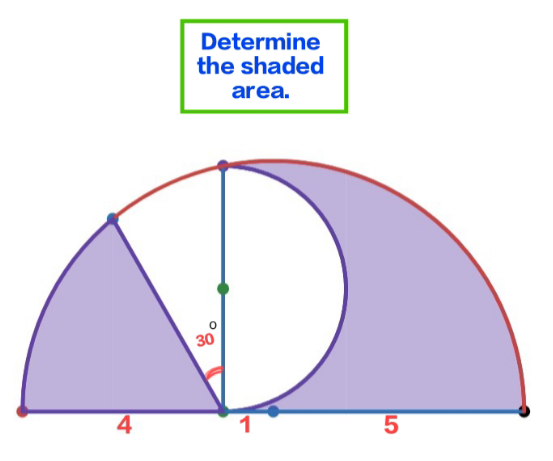
Question Number 218349 by Hanuda354 last updated on 07/Apr/25
Answered by vnm last updated on 07/Apr/25
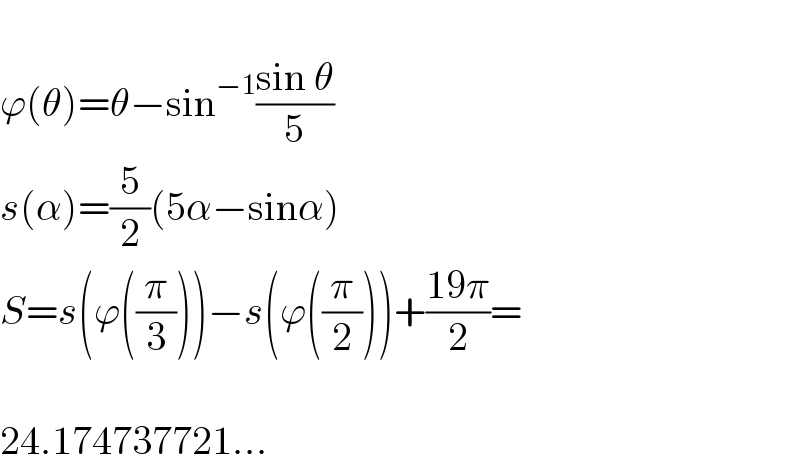
$$ \\ $$$$\varphi\left(\theta\right)=\theta−\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{sin}\:\theta}{\mathrm{5}} \\ $$$${s}\left(\alpha\right)=\frac{\mathrm{5}}{\mathrm{2}}\left(\mathrm{5}\alpha−\mathrm{sin}\alpha\right) \\ $$$${S}={s}\left(\varphi\left(\frac{\pi}{\mathrm{3}}\right)\right)−{s}\left(\varphi\left(\frac{\pi}{\mathrm{2}}\right)\right)+\frac{\mathrm{19}\pi}{\mathrm{2}}= \\ $$$$ \\ $$$$\mathrm{24}.\mathrm{174737721}... \\ $$
Commented by Hanuda354 last updated on 07/Apr/25

$$\mathrm{Thanks} \\ $$
Answered by mr W last updated on 08/Apr/25
Commented by mr W last updated on 08/Apr/25
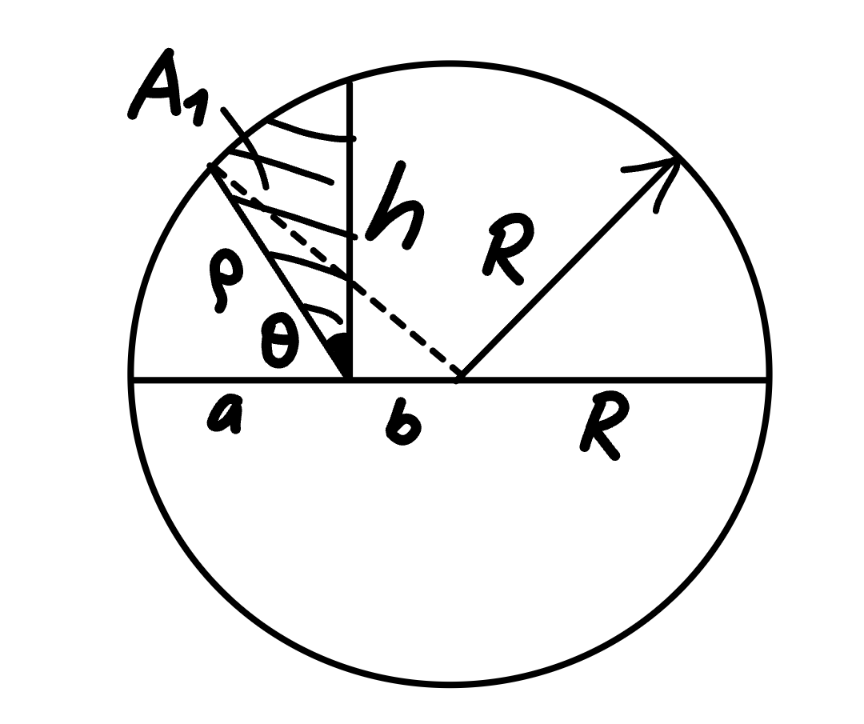
![R^2 =ρ^2 +b^2 −2bρ cos ((π/2)+θ) ρ^2 +2bρ sin θ−(R^2 −b^2 )=0 ρ=−b sin θ+(√(R^2 −b^2 cos^2 θ)) A_1 =(1/2)∫_0 ^θ ρ^2 dθ =(1/2)∫_0 ^θ (R^2 −b^2 cos 2θ−2b sin θ(√(R^2 −b^2 cos^2 θ)) )dθ =((R^2 θ)/2)−((b^2 sin 2θ)/4)+R^2 ∫_0 ^θ (√(1−(((b cos θ)/R))^2 )) d(((b cos θ)/R)) =((R^2 θ)/2)−((b^2 sin 2θ)/4)+(R^2 /2)[sin^(−1) ((b cos θ)/R)+((b cos θ)/R)(√(1−(((b cos θ)/R))^2 ))]_0 ^θ =((R^2 θ)/2)−((b^2 sin 2θ)/4)−(R^2 /2)[sin^(−1) (b/R)−sin^(−1) ((b cos θ)/R)+(b/R)(√(1−(b^2 /R^2 )))−((b cos θ)/R)(√(1−(((b cos θ)/R))^2 ))] =(R^2 /2)(θ−sin^(−1) (b/R)+sin^(−1) ((b cos θ)/R))−((b^2 sin 2θ)/4)−((bR)/2)[(√(1−(b^2 /R^2 )))−cos θ(√(1−(((b cos θ)/R))^2 ))] with b=1, R=5, θ=(π/6) A_1 =((25)/2)((π/6)−sin^(−1) (1/5)+sin^(−1) ((√3)/(10)))−((√3)/8)−(5/2)((√(1−(1/(25))))−((√3)/2)(√(1−(3/(100))))) ≈5.670392 h^2 =a(b+R)=4×(1+5)=24 ⇒r=(h/2)=(√6) A_(shade) =((πR^2 )/2)−((πr^2 )/2)−A_1 =((π×5^2 )/2)−((π×6)/2)−A_1 ≈24.174738](Q218379.png)
$${R}^{\mathrm{2}} =\rho^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{b}\rho\:\mathrm{cos}\:\left(\frac{\pi}{\mathrm{2}}+\theta\right) \\ $$$$\rho^{\mathrm{2}} +\mathrm{2}{b}\rho\:\mathrm{sin}\:\theta−\left({R}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\rho=−{b}\:\mathrm{sin}\:\theta+\sqrt{{R}^{\mathrm{2}} −{b}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta} \\ $$$${A}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\theta} \rho^{\mathrm{2}} {d}\theta \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\theta} \left({R}^{\mathrm{2}} −{b}^{\mathrm{2}} \mathrm{cos}\:\mathrm{2}\theta−\mathrm{2}{b}\:\mathrm{sin}\:\theta\sqrt{{R}^{\mathrm{2}} −{b}^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\theta}\:\right){d}\theta \\ $$$$\:\:\:=\frac{{R}^{\mathrm{2}} \theta}{\mathrm{2}}−\frac{{b}^{\mathrm{2}} \mathrm{sin}\:\mathrm{2}\theta}{\mathrm{4}}+{R}^{\mathrm{2}} \int_{\mathrm{0}} ^{\theta} \sqrt{\mathrm{1}−\left(\frac{{b}\:\mathrm{cos}\:\theta}{{R}}\right)^{\mathrm{2}} }\:{d}\left(\frac{{b}\:\mathrm{cos}\:\theta}{{R}}\right) \\ $$$$\:\:\:=\frac{{R}^{\mathrm{2}} \theta}{\mathrm{2}}−\frac{{b}^{\mathrm{2}} \mathrm{sin}\:\mathrm{2}\theta}{\mathrm{4}}+\frac{{R}^{\mathrm{2}} }{\mathrm{2}}\left[\mathrm{sin}^{−\mathrm{1}} \frac{{b}\:\mathrm{cos}\:\theta}{{R}}+\frac{{b}\:\mathrm{cos}\:\theta}{{R}}\sqrt{\mathrm{1}−\left(\frac{{b}\:\mathrm{cos}\:\theta}{{R}}\right)^{\mathrm{2}} }\right]_{\mathrm{0}} ^{\theta} \\ $$$$\:\:\:=\frac{{R}^{\mathrm{2}} \theta}{\mathrm{2}}−\frac{{b}^{\mathrm{2}} \mathrm{sin}\:\mathrm{2}\theta}{\mathrm{4}}−\frac{{R}^{\mathrm{2}} }{\mathrm{2}}\left[\mathrm{sin}^{−\mathrm{1}} \frac{{b}}{{R}}−\mathrm{sin}^{−\mathrm{1}} \frac{{b}\:\mathrm{cos}\:\theta}{{R}}+\frac{{b}}{{R}}\sqrt{\mathrm{1}−\frac{{b}^{\mathrm{2}} }{{R}^{\mathrm{2}} }}−\frac{{b}\:\mathrm{cos}\:\theta}{{R}}\sqrt{\mathrm{1}−\left(\frac{{b}\:\mathrm{cos}\:\theta}{{R}}\right)^{\mathrm{2}} }\right] \\ $$$$\:\:\:=\frac{{R}^{\mathrm{2}} }{\mathrm{2}}\left(\theta−\mathrm{sin}^{−\mathrm{1}} \frac{{b}}{{R}}+\mathrm{sin}^{−\mathrm{1}} \frac{{b}\:\mathrm{cos}\:\theta}{{R}}\right)−\frac{{b}^{\mathrm{2}} \mathrm{sin}\:\mathrm{2}\theta}{\mathrm{4}}−\frac{{bR}}{\mathrm{2}}\left[\sqrt{\mathrm{1}−\frac{{b}^{\mathrm{2}} }{{R}^{\mathrm{2}} }}−\mathrm{cos}\:\theta\sqrt{\mathrm{1}−\left(\frac{{b}\:\mathrm{cos}\:\theta}{{R}}\right)^{\mathrm{2}} }\right] \\ $$$${with}\:{b}=\mathrm{1},\:{R}=\mathrm{5},\:\theta=\frac{\pi}{\mathrm{6}} \\ $$$${A}_{\mathrm{1}} =\frac{\mathrm{25}}{\mathrm{2}}\left(\frac{\pi}{\mathrm{6}}−\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{5}}+\mathrm{sin}^{−\mathrm{1}} \frac{\sqrt{\mathrm{3}}}{\mathrm{10}}\right)−\frac{\sqrt{\mathrm{3}}}{\mathrm{8}}−\frac{\mathrm{5}}{\mathrm{2}}\left(\sqrt{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{25}}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\sqrt{\mathrm{1}−\frac{\mathrm{3}}{\mathrm{100}}}\right) \\ $$$$\:\:\:\:\:\approx\mathrm{5}.\mathrm{670392} \\ $$$$ \\ $$$${h}^{\mathrm{2}} ={a}\left({b}+{R}\right)=\mathrm{4}×\left(\mathrm{1}+\mathrm{5}\right)=\mathrm{24} \\ $$$$\Rightarrow{r}=\frac{{h}}{\mathrm{2}}=\sqrt{\mathrm{6}} \\ $$$${A}_{{shade}} =\frac{\pi{R}^{\mathrm{2}} }{\mathrm{2}}−\frac{\pi{r}^{\mathrm{2}} }{\mathrm{2}}−{A}_{\mathrm{1}} \\ $$$$\:\:\:=\frac{\pi×\mathrm{5}^{\mathrm{2}} }{\mathrm{2}}−\frac{\pi×\mathrm{6}}{\mathrm{2}}−{A}_{\mathrm{1}} \\ $$$$\:\:\:\approx\mathrm{24}.\mathrm{174738} \\ $$
Commented by Hanuda354 last updated on 08/Apr/25

$$\mathrm{Nice}!!!\:\mathrm{Thnks} \\ $$
Answered by mr W last updated on 09/Apr/25
Commented by mr W last updated on 09/Apr/25
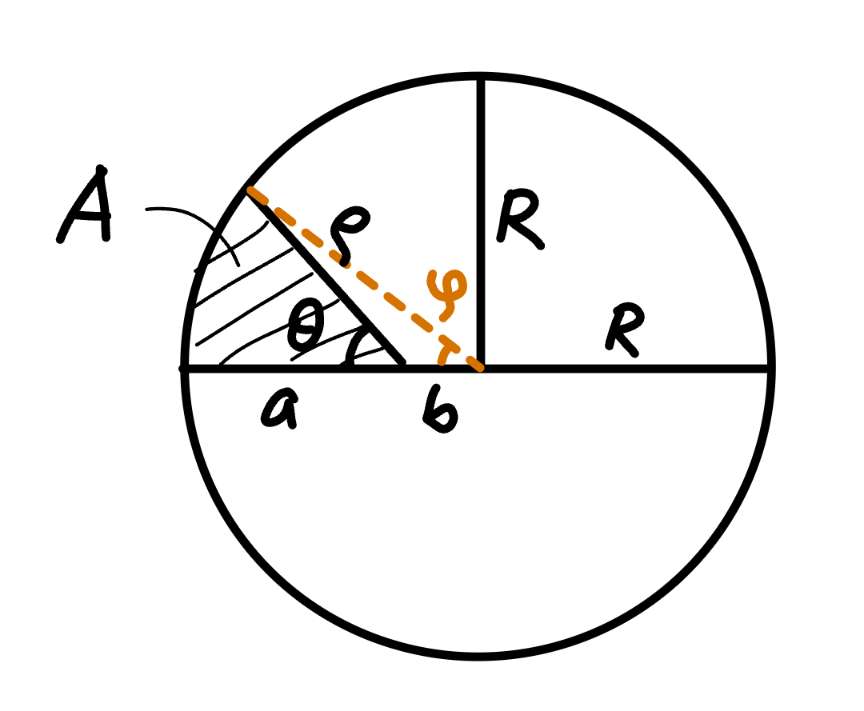
![((sin (θ−ϕ))/b)=((sin θ)/R) ⇒ϕ=θ−sin^(−1) ((b sin θ)/R) A=((R^2 ϕ)/2)−((bR sin ϕ)/2)=(R^2 /2)(ϕ−((b sin ϕ)/R)) A=(R^2 /2)[θ−sin^(−1) ((b sin θ)/R)−(b/R) sin (θ−sin^(−1) ((b sin θ)/R))] A_1 =A∣_(θ=(π/2)) −A∣_(θ=(π/3)) =(5^2 /2)[(π/2)−sin^(−1) (1/5)−(1/5) sin ((π/2)−sin^(−1) (1/5))] −(5^2 /2)[(π/3)−sin^(−1) (( (√3))/(10))−(1/5) sin ((π/3)−sin^(−1) ((√3)/(10)))] =(5^2 /2)[(π/6)−sin^(−1) (1/5)+sin^(−1) ((√3)/(10))−(1/5) cos (sin^(−1) (1/5))+(1/5) sin ((π/3)−sin^(−1) ((√3)/(10)))] ≈5.679392 A_(shade) =((π×5^2 )/2)−((π×((√6))^2 )/2)−A_1 ≈24.174738](Q218416.png)
$$\frac{\mathrm{sin}\:\left(\theta−\varphi\right)}{{b}}=\frac{\mathrm{sin}\:\theta}{{R}} \\ $$$$\Rightarrow\varphi=\theta−\mathrm{sin}^{−\mathrm{1}} \frac{{b}\:\mathrm{sin}\:\theta}{{R}} \\ $$$${A}=\frac{{R}^{\mathrm{2}} \varphi}{\mathrm{2}}−\frac{{bR}\:\mathrm{sin}\:\varphi}{\mathrm{2}}=\frac{{R}^{\mathrm{2}} }{\mathrm{2}}\left(\varphi−\frac{{b}\:\mathrm{sin}\:\varphi}{{R}}\right) \\ $$$${A}=\frac{{R}^{\mathrm{2}} }{\mathrm{2}}\left[\theta−\mathrm{sin}^{−\mathrm{1}} \frac{{b}\:\mathrm{sin}\:\theta}{{R}}−\frac{{b}}{{R}}\:\mathrm{sin}\:\left(\theta−\mathrm{sin}^{−\mathrm{1}} \frac{{b}\:\mathrm{sin}\:\theta}{{R}}\right)\right] \\ $$$${A}_{\mathrm{1}} ={A}\mid_{\theta=\frac{\pi}{\mathrm{2}}} −{A}\mid_{\theta=\frac{\pi}{\mathrm{3}}} \\ $$$$\:\:\:\:\:=\frac{\mathrm{5}^{\mathrm{2}} }{\mathrm{2}}\left[\frac{\pi}{\mathrm{2}}−\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{5}}\:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{5}}\right)\right] \\ $$$$\:\:\:\:\:\:\:\:−\frac{\mathrm{5}^{\mathrm{2}} }{\mathrm{2}}\left[\frac{\pi}{\mathrm{3}}−\mathrm{sin}^{−\mathrm{1}} \frac{\:\sqrt{\mathrm{3}}}{\mathrm{10}}−\frac{\mathrm{1}}{\mathrm{5}}\:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}−\mathrm{sin}^{−\mathrm{1}} \frac{\sqrt{\mathrm{3}}}{\mathrm{10}}\right)\right] \\ $$$$\:\:\:\:\:=\frac{\mathrm{5}^{\mathrm{2}} }{\mathrm{2}}\left[\frac{\pi}{\mathrm{6}}−\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{5}}+\mathrm{sin}^{−\mathrm{1}} \frac{\sqrt{\mathrm{3}}}{\mathrm{10}}−\frac{\mathrm{1}}{\mathrm{5}}\:\mathrm{cos}\:\:\left(\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{5}}\right)+\frac{\mathrm{1}}{\mathrm{5}}\:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}−\mathrm{sin}^{−\mathrm{1}} \frac{\sqrt{\mathrm{3}}}{\mathrm{10}}\right)\right] \\ $$$$\:\:\:\:\:\approx\mathrm{5}.\mathrm{679392} \\ $$$${A}_{{shade}} =\frac{\pi×\mathrm{5}^{\mathrm{2}} }{\mathrm{2}}−\frac{\pi×\left(\sqrt{\mathrm{6}}\right)^{\mathrm{2}} }{\mathrm{2}}−{A}_{\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\approx\mathrm{24}.\mathrm{174738} \\ $$
