Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 218318 by Tawa11 last updated on 06/Apr/25

Commented by Tawa11 last updated on 06/Apr/25

Area of circle.

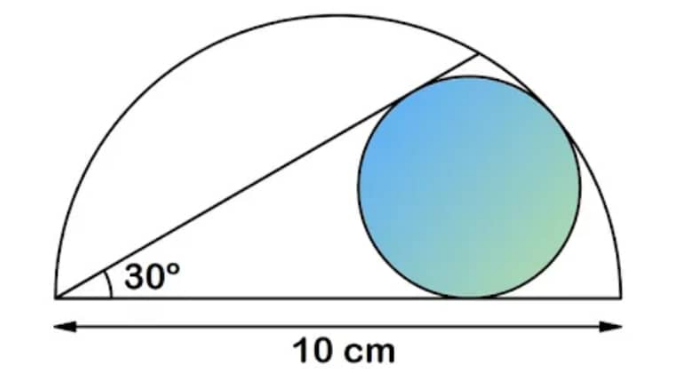
$$\mathrm{Area}\:\mathrm{of}\:\mathrm{circle}. \\ $$

Commented by AlagaIbile last updated on 06/Apr/25

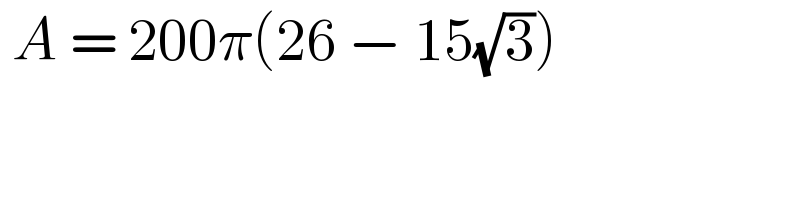
A = 200π(26 − 15(√3))

$$\:{A}\:=\:\mathrm{200}\pi\left(\mathrm{26}\:−\:\mathrm{15}\sqrt{\mathrm{3}}\right) \\ $$

Commented by Tawa11 last updated on 06/Apr/25

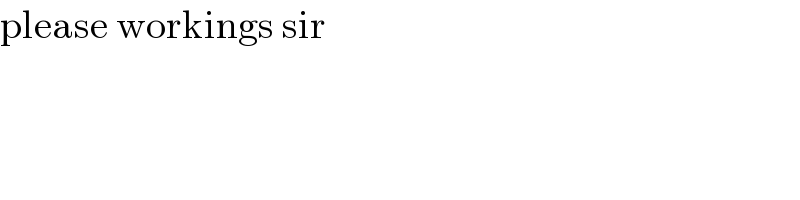
please workings sir

$$\mathrm{please}\:\mathrm{workings}\:\mathrm{sir} \\ $$

Answered by mr W last updated on 06/Apr/25

Commented by mr W last updated on 06/Apr/25

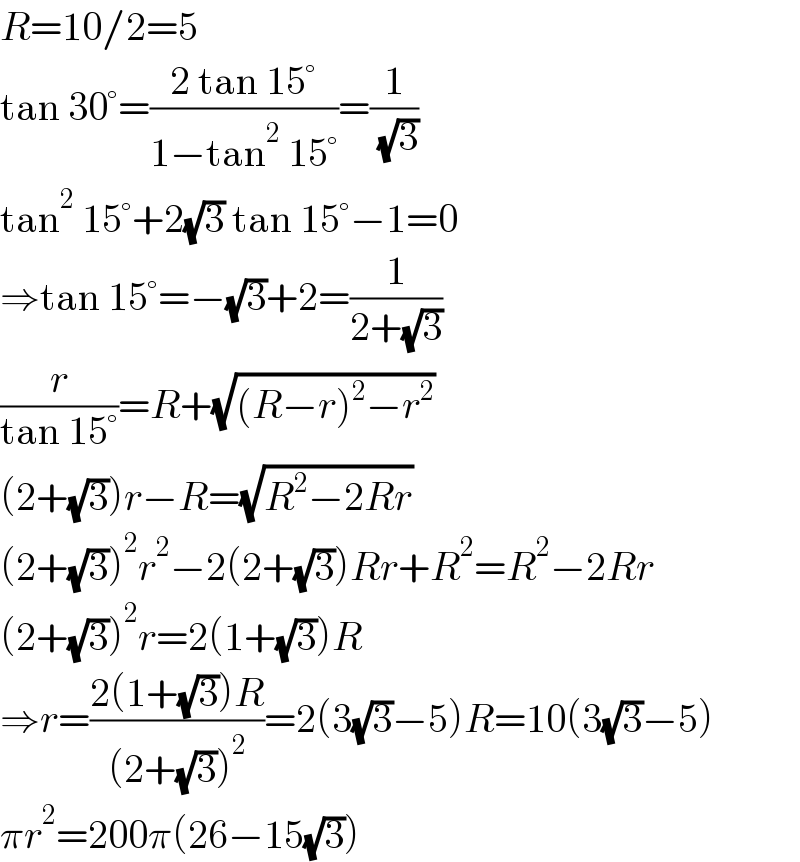
R=10/2=5 tan 30°=((2 tan 15°)/(1−tan^2 15°))=(1/( (√3))) tan^2 15°+2(√3) tan 15°−1=0 ⇒tan 15°=−(√3)+2=(1/(2+(√3))) (r/(tan 15°))=R+(√((R−r)^2 −r^2 )) (2+(√3))r−R=(√(R^2 −2Rr)) (2+(√3))^2 r^2 −2(2+(√3))Rr+R^2 =R^2 −2Rr (2+(√3))^2 r=2(1+(√3))R ⇒r=((2(1+(√3))R)/((2+(√3))^2 ))=2(3(√3)−5)R=10(3(√3)−5) πr^2 =200π(26−15(√3))

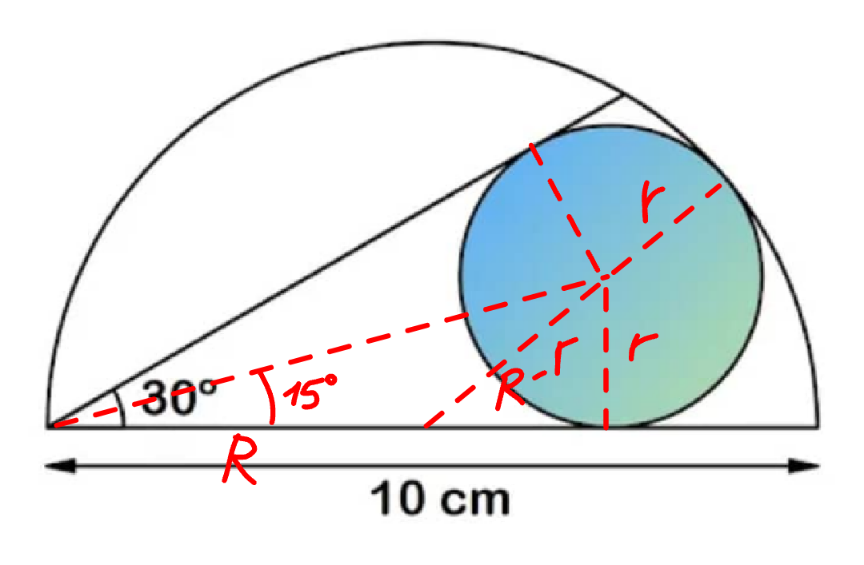
$${R}=\mathrm{10}/\mathrm{2}=\mathrm{5} \\ $$$$\mathrm{tan}\:\mathrm{30}°=\frac{\mathrm{2}\:\mathrm{tan}\:\mathrm{15}°}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\mathrm{15}°}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$$\mathrm{tan}^{\mathrm{2}} \:\mathrm{15}°+\mathrm{2}\sqrt{\mathrm{3}}\:\mathrm{tan}\:\mathrm{15}°−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{tan}\:\mathrm{15}°=−\sqrt{\mathrm{3}}+\mathrm{2}=\frac{\mathrm{1}}{\mathrm{2}+\sqrt{\mathrm{3}}} \\ $$$$\frac{{r}}{\mathrm{tan}\:\mathrm{15}°}={R}+\sqrt{\left({R}−{r}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} } \\ $$$$\left(\mathrm{2}+\sqrt{\mathrm{3}}\right){r}−{R}=\sqrt{{R}^{\mathrm{2}} −\mathrm{2}{Rr}} \\ $$$$\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{2}} {r}^{\mathrm{2}} −\mathrm{2}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right){Rr}+{R}^{\mathrm{2}} ={R}^{\mathrm{2}} −\mathrm{2}{Rr} \\ $$$$\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{2}} {r}=\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{3}}\right){R} \\ $$$$\Rightarrow{r}=\frac{\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{3}}\right){R}}{\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }=\mathrm{2}\left(\mathrm{3}\sqrt{\mathrm{3}}−\mathrm{5}\right){R}=\mathrm{10}\left(\mathrm{3}\sqrt{\mathrm{3}}−\mathrm{5}\right) \\ $$$$\pi{r}^{\mathrm{2}} =\mathrm{200}\pi\left(\mathrm{26}−\mathrm{15}\sqrt{\mathrm{3}}\right) \\ $$

Commented by Tawa11 last updated on 07/Apr/25

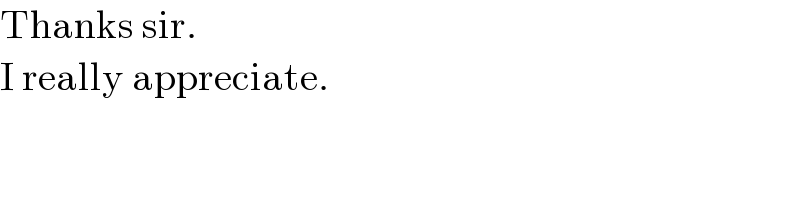
Thanks sir. I really appreciate.

$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$$$\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com