Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

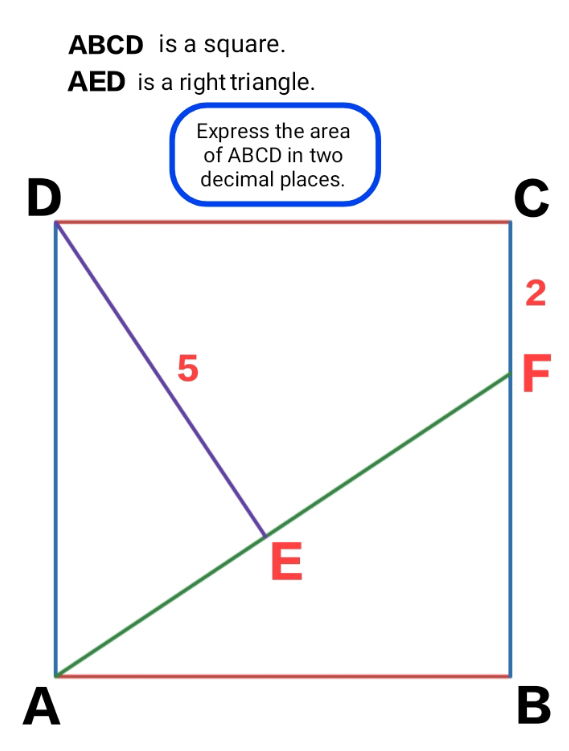
Question Number 218317 by Hanuda354 last updated on 06/Apr/25

Answered by mr W last updated on 06/Apr/25

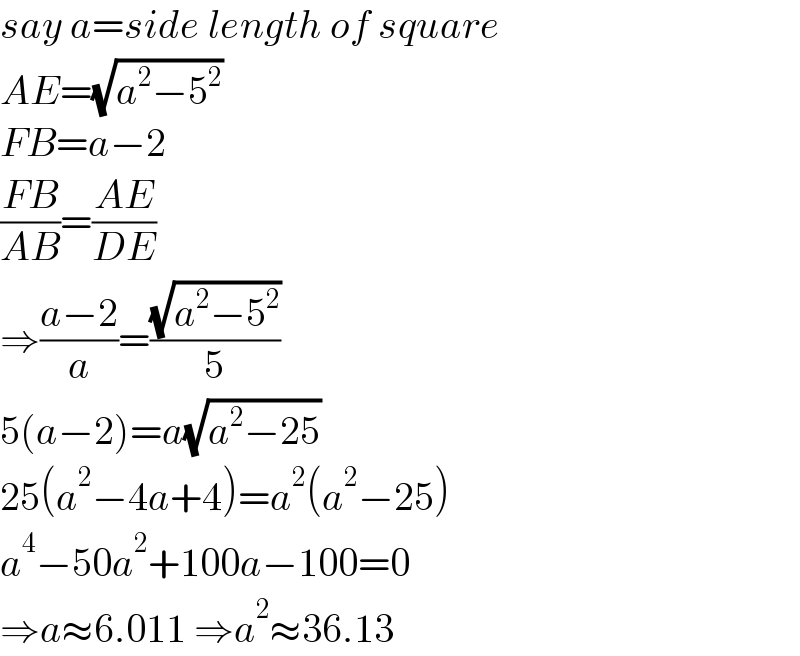
say a=side length of square AE=(√(a^2 −5^2 )) FB=a−2 ((FB)/(AB))=((AE)/(DE)) ⇒((a−2)/a)=((√(a^2 −5^2 ))/5) 5(a−2)=a(√(a^2 −25)) 25(a^2 −4a+4)=a^2 (a^2 −25) a^4 −50a^2 +100a−100=0 ⇒a≈6.011 ⇒a^2 ≈36.13

$${say}\:{a}={side}\:{length}\:{of}\:{square} \\ $$$${AE}=\sqrt{{a}^{\mathrm{2}} −\mathrm{5}^{\mathrm{2}} } \\ $$$${FB}={a}−\mathrm{2} \\ $$$$\frac{{FB}}{{AB}}=\frac{{AE}}{{DE}} \\ $$$$\Rightarrow\frac{{a}−\mathrm{2}}{{a}}=\frac{\sqrt{{a}^{\mathrm{2}} −\mathrm{5}^{\mathrm{2}} }}{\mathrm{5}} \\ $$$$\mathrm{5}\left({a}−\mathrm{2}\right)={a}\sqrt{{a}^{\mathrm{2}} −\mathrm{25}} \\ $$$$\mathrm{25}\left({a}^{\mathrm{2}} −\mathrm{4}{a}+\mathrm{4}\right)={a}^{\mathrm{2}} \left({a}^{\mathrm{2}} −\mathrm{25}\right) \\ $$$${a}^{\mathrm{4}} −\mathrm{50}{a}^{\mathrm{2}} +\mathrm{100}{a}−\mathrm{100}=\mathrm{0} \\ $$$$\Rightarrow{a}\approx\mathrm{6}.\mathrm{011}\:\Rightarrow{a}^{\mathrm{2}} \approx\mathrm{36}.\mathrm{13} \\ $$

Commented by Hanuda354 last updated on 07/Apr/25

Thank you, sir.

$$\mathrm{Thank}\:\mathrm{you},\:\mathrm{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com