
Previous in Relation and Functions Next in Relation and Functions
Question Number 218311 by mr W last updated on 06/Apr/25
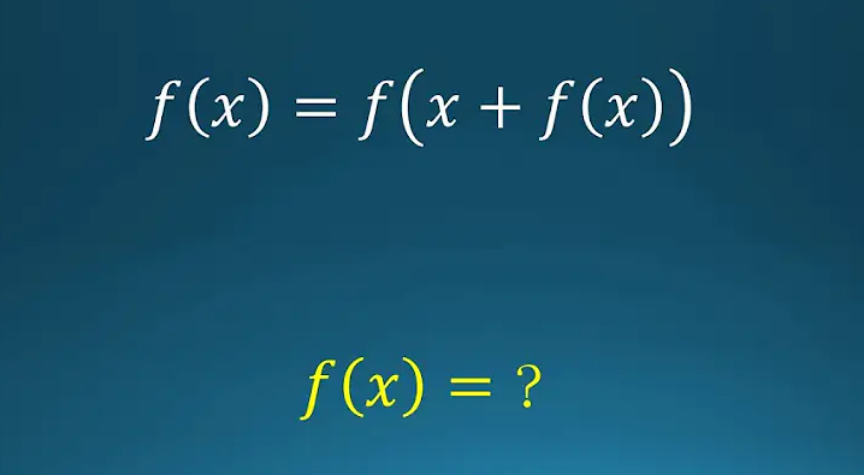
Answered by Frix last updated on 06/Apr/25

$${f}\left({x}\right)={c} \\ $$
Commented by mr W last updated on 06/Apr/25
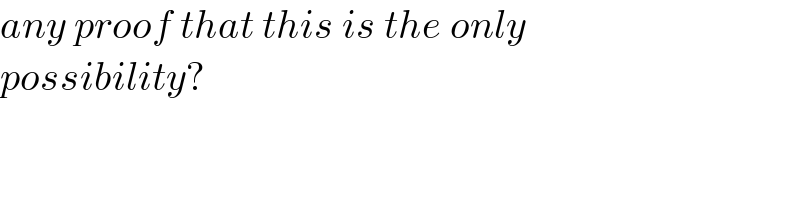
$${any}\:{proof}\:{that}\:{this}\:{is}\:{the}\:{only} \\ $$$${possibility}? \\ $$
Commented by Frix last updated on 06/Apr/25

$$\mathrm{It}\:\mathrm{seems}\:\mathrm{obvious}\:\mathrm{to}\:\mathrm{me}... \\ $$$$\mathrm{Try}\:\mathrm{any}\:\mathrm{function}\:\mathrm{to}\:\mathrm{see}\:\mathrm{what}\:\mathrm{happens}: \\ $$$${f}\left({x}\right)={kx}+{d} \\ $$$${kx}+{d}={x}+{k}\left({kx}+{d}\right)+{d} \\ $$$${f}\left({x}\right)=\mathrm{sin}\:{x} \\ $$$$\left.\mathrm{sin}\:{x}\:=\mathrm{sin}\:\left({x}+\mathrm{sin}\:{x}\right)\right) \\ $$$${f}\left({x}\right)={x}^{{r}} \\ $$$${x}^{{r}} =\left({x}+{x}^{{r}} \right)^{{r}} \\ $$$${f}\left({x}\right)=\mathrm{e}^{{x}} \\ $$$$\mathrm{e}^{{x}} =\mathrm{e}^{{x}+\mathrm{e}^{{x}} } \\ $$$${f}\left({x}\right)=\mathrm{ln}\:{x} \\ $$$$\mathrm{ln}\:{x}\:=\mathrm{ln}\:\left({x}+\mathrm{ln}\:{x}\right) \\ $$$$\mathrm{All}\:\mathrm{of}\:\mathrm{these}\:\mathrm{can}\:\mathrm{be}\:\mathrm{solved}\:\mathrm{for}\:{x}\:\mathrm{but}\:\mathrm{they} \\ $$$$\mathrm{never}\:\mathrm{are}\:\mathrm{true}\:\mathrm{for}\:\mathrm{all}\:{x} \\ $$
