Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 218267 by lmcp1203 last updated on 04/Apr/25

Commented by lmcp1203 last updated on 04/Apr/25

thanks

$${thanks} \\ $$

Answered by vnm last updated on 04/Apr/25

Nothing has changed with the drawings, they still won′t load.The dot on the left is A, on the top is B, on the right is C and at the bottom in the middle is D. let AC=1, AD=BC=a ∡ABC=120° ((AC)/(sin ∡ABC))=((BC)/(sin∡BAC )) a=BC=AC((sin ∡BAC)/(sin ∡ABC))=((sin (60°−2x))/(sin 120^° ))= (((√3)cos 2x−sin 2x)/( (√3))) ((BC)/(sin ∡BDC))=((CD)/(sin ∡CBD)) (a/(sin(180°−3x) ))=((1−a)/(sin x)) ((((√3)cos 2x−sin 2x)/( (√3)))/(sin 3x))=((1−(((√3)cos 2x−sin 2x)/( (√3))))/(sin x)) 2x=t (√3)(2cos^2 t−1)=2sin t∙(1+cos t) 16cos^4 t+8cos^3 t−12cos^2 t−8cos t−1=0 2cos t=u u^4 +u^3 −3u^2 −4u−1=0 u^3 (u+1)−(3u+1)(u+1)=0 (u^3 −3u−1)(u+1)=0 u^3 −3u−1=0 (1/2)=cos 60°=cos (3∙20°)= cos 40°cos 20°−sin 40^° sin 20°= (2cos^2 20°−1)cos 20°− 2cos 20^° (1−cos^2 20°)= 4cos^3 20°−3cos 20^° (2cos 20°)^3 −3(2cos 20°)−1=0 x=10°

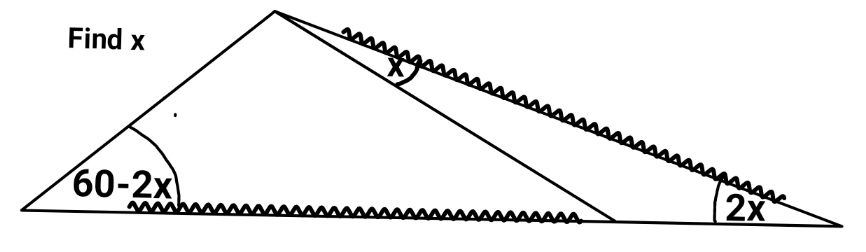
$$ \\ $$$$\mathrm{Nothing}\:\mathrm{has}\:\mathrm{changed}\:\mathrm{with}\:\mathrm{the} \\ $$$$\mathrm{drawings},\:\mathrm{they}\:\mathrm{still}\:\mathrm{won}'\mathrm{t} \\ $$$$\mathrm{load}.\mathrm{The}\:\mathrm{dot}\:\mathrm{on}\:\mathrm{the}\:\mathrm{left}\:\mathrm{is}\:\mathrm{A},\:\mathrm{on} \\ $$$$\mathrm{the}\:\mathrm{top}\:\mathrm{is}\:\mathrm{B},\:\mathrm{on}\:\mathrm{the}\:\mathrm{right}\:\mathrm{is}\:\mathrm{C}\: \\ $$$$\mathrm{and}\:\mathrm{at}\:\mathrm{the}\:\mathrm{bottom}\:\mathrm{in}\:\mathrm{the}\: \\ $$$$\mathrm{middle}\:\mathrm{is}\:\mathrm{D}. \\ $$$${let}\:{AC}=\mathrm{1},\:{AD}={BC}={a} \\ $$$$\measuredangle{ABC}=\mathrm{120}° \\ $$$$\frac{{AC}}{\mathrm{sin}\:\measuredangle{ABC}}=\frac{{BC}}{\mathrm{sin}\measuredangle{BAC}\:} \\ $$$${a}={BC}={AC}\frac{\mathrm{sin}\:\measuredangle{BAC}}{\mathrm{sin}\:\measuredangle{ABC}}=\frac{\mathrm{sin}\:\left(\mathrm{60}°−\mathrm{2}{x}\right)}{\mathrm{sin}\:\mathrm{120}^{°} }= \\ $$$$\frac{\sqrt{\mathrm{3}}\mathrm{cos}\:\mathrm{2}{x}−\mathrm{sin}\:\mathrm{2}{x}}{\:\sqrt{\mathrm{3}}} \\ $$$$\frac{{BC}}{\mathrm{sin}\:\measuredangle{BDC}}=\frac{{CD}}{\mathrm{sin}\:\measuredangle{CBD}} \\ $$$$\frac{{a}}{\mathrm{sin}\left(\mathrm{180}°−\mathrm{3}{x}\right)\:}=\frac{\mathrm{1}−{a}}{\mathrm{sin}\:{x}} \\ $$$$\frac{\frac{\sqrt{\mathrm{3}}\mathrm{cos}\:\mathrm{2}{x}−\mathrm{sin}\:\mathrm{2}{x}}{\:\sqrt{\mathrm{3}}}}{\mathrm{sin}\:\mathrm{3}{x}}=\frac{\mathrm{1}−\frac{\sqrt{\mathrm{3}}\mathrm{cos}\:\mathrm{2}{x}−\mathrm{sin}\:\mathrm{2}{x}}{\:\sqrt{\mathrm{3}}}}{\mathrm{sin}\:{x}} \\ $$$$ \\ $$$$\mathrm{2}{x}={t} \\ $$$$\sqrt{\mathrm{3}}\left(\mathrm{2cos}^{\mathrm{2}} {t}−\mathrm{1}\right)=\mathrm{2sin}\:{t}\centerdot\left(\mathrm{1}+\mathrm{cos}\:{t}\right) \\ $$$$\mathrm{16cos}^{\mathrm{4}} {t}+\mathrm{8cos}^{\mathrm{3}} {t}−\mathrm{12cos}^{\mathrm{2}} {t}−\mathrm{8cos}\:{t}−\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{2cos}\:{t}={u} \\ $$$${u}^{\mathrm{4}} +{u}^{\mathrm{3}} −\mathrm{3}{u}^{\mathrm{2}} −\mathrm{4}{u}−\mathrm{1}=\mathrm{0} \\ $$$${u}^{\mathrm{3}} \left({u}+\mathrm{1}\right)−\left(\mathrm{3}{u}+\mathrm{1}\right)\left({u}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\left({u}^{\mathrm{3}} −\mathrm{3}{u}−\mathrm{1}\right)\left({u}+\mathrm{1}\right)=\mathrm{0} \\ $$$${u}^{\mathrm{3}} −\mathrm{3}{u}−\mathrm{1}=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{cos}\:\mathrm{60}°=\mathrm{cos}\:\left(\mathrm{3}\centerdot\mathrm{20}°\right)= \\ $$$$\mathrm{cos}\:\mathrm{40}°\mathrm{cos}\:\mathrm{20}°−\mathrm{sin}\:\mathrm{40}^{°} \mathrm{sin}\:\mathrm{20}°= \\ $$$$\left(\mathrm{2cos}^{\mathrm{2}} \mathrm{20}°−\mathrm{1}\right)\mathrm{cos}\:\mathrm{20}°− \\ $$$$\mathrm{2cos}\:\mathrm{20}^{°} \left(\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \mathrm{20}°\right)= \\ $$$$\mathrm{4cos}^{\mathrm{3}} \mathrm{20}°−\mathrm{3cos}\:\mathrm{20}^{°} \\ $$$$\left(\mathrm{2cos}\:\mathrm{20}°\right)^{\mathrm{3}} −\mathrm{3}\left(\mathrm{2cos}\:\mathrm{20}°\right)−\mathrm{1}=\mathrm{0} \\ $$$${x}=\mathrm{10}° \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com