
Question Number 218262 by hardmath last updated on 03/Apr/25
Commented by hardmath last updated on 03/Apr/25
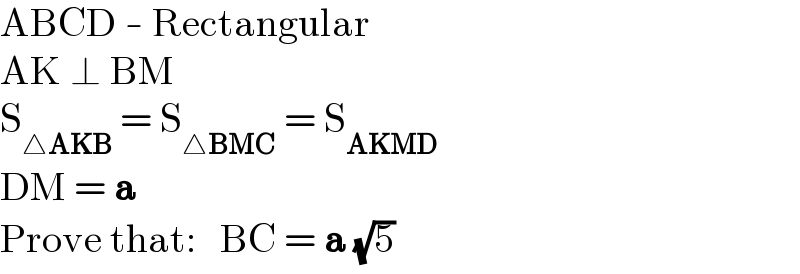
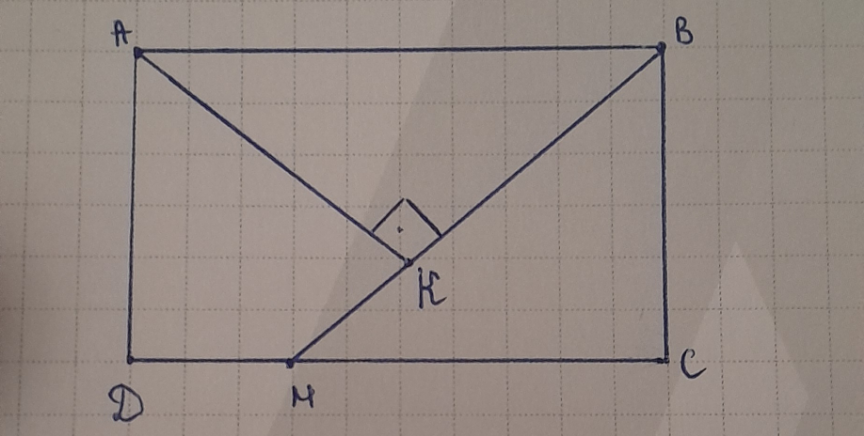
$$\mathrm{ABCD}\:-\:\mathrm{Rectangular} \\ $$$$\mathrm{AK}\:\bot\:\mathrm{BM} \\ $$$$\mathrm{S}_{\bigtriangleup\boldsymbol{\mathrm{AKB}}} \:=\:\mathrm{S}_{\bigtriangleup\boldsymbol{\mathrm{BMC}}} \:=\:\mathrm{S}_{\boldsymbol{\mathrm{AKMD}}} \\ $$$$\mathrm{DM}\:=\:\boldsymbol{\mathrm{a}} \\ $$$$\mathrm{Prove}\:\mathrm{that}:\:\:\:\mathrm{BC}\:=\:\boldsymbol{\mathrm{a}}\:\sqrt{\mathrm{5}} \\ $$
Answered by mr W last updated on 04/Apr/25
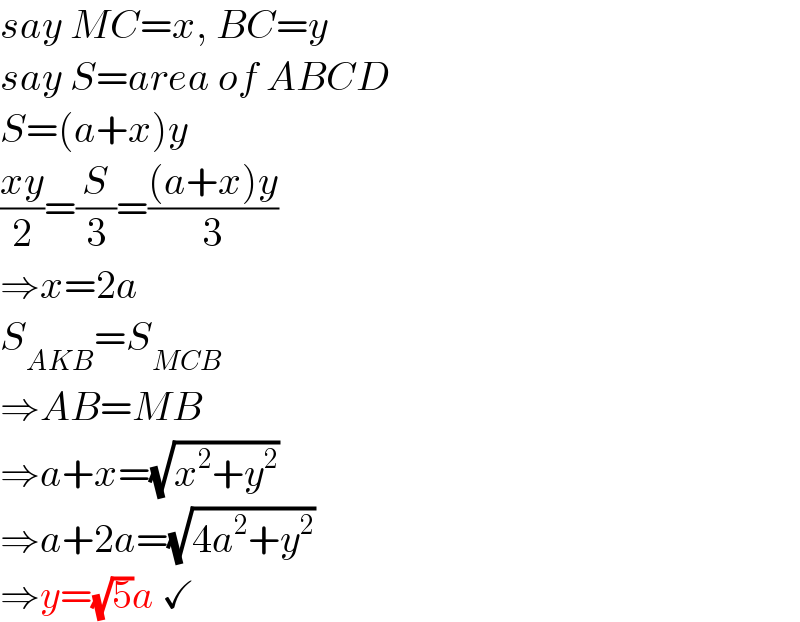
$${say}\:{MC}={x},\:{BC}={y} \\ $$$${say}\:{S}={area}\:{of}\:{ABCD} \\ $$$${S}=\left({a}+{x}\right){y} \\ $$$$\frac{{xy}}{\mathrm{2}}=\frac{{S}}{\mathrm{3}}=\frac{\left({a}+{x}\right){y}}{\mathrm{3}} \\ $$$$\Rightarrow{x}=\mathrm{2}{a} \\ $$$${S}_{{AKB}} ={S}_{{MCB}} \: \\ $$$$\Rightarrow{AB}={MB} \\ $$$$\Rightarrow{a}+{x}=\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} } \\ $$$$\Rightarrow{a}+\mathrm{2}{a}=\sqrt{\mathrm{4}{a}^{\mathrm{2}} +{y}^{\mathrm{2}} } \\ $$$$\Rightarrow{y}=\sqrt{\mathrm{5}}{a}\:\checkmark \\ $$
Commented by mehdee7396 last updated on 05/Apr/25

$$ \\ $$$${thank}\:{you}.{i}\:{understand} \\ $$$$\blacktriangleright\:\:\angle{ABK}=\angle{BMC}\:\:\:\blacktriangleleft \\ $$$$ \\ $$
Commented by hardmath last updated on 04/Apr/25
$$\mathrm{thankyou}\:\mathrm{dear}\:\mathrm{professor} \\ $$
Commented by mehdee7396 last updated on 05/Apr/25

$$ \\ $$$$\Rightarrow?\:{AB}={MB} \\ $$
Commented by hardmath last updated on 05/Apr/25
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{dear}\:\mathrm{professor} \\ $$
Commented by mr W last updated on 05/Apr/25
Commented by mr W last updated on 05/Apr/25
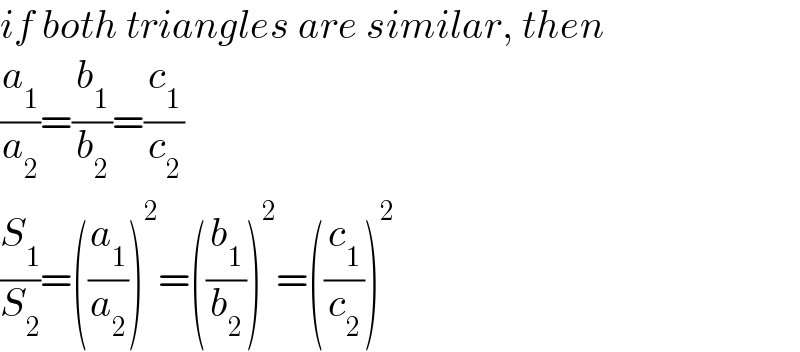
$${if}\:{both}\:{triangles}\:{are}\:{similar},\:{then} \\ $$$$\frac{{a}_{\mathrm{1}} }{{a}_{\mathrm{2}} }=\frac{{b}_{\mathrm{1}} }{{b}_{\mathrm{2}} }=\frac{{c}_{\mathrm{1}} }{{c}_{\mathrm{2}} } \\ $$$$\frac{{S}_{\mathrm{1}} }{{S}_{\mathrm{2}} }=\left(\frac{{a}_{\mathrm{1}} }{{a}_{\mathrm{2}} }\right)^{\mathrm{2}} =\left(\frac{{b}_{\mathrm{1}} }{{b}_{\mathrm{2}} }\right)^{\mathrm{2}} =\left(\frac{{c}_{\mathrm{1}} }{{c}_{\mathrm{2}} }\right)^{\mathrm{2}} \\ $$
Commented by mr W last updated on 05/Apr/25
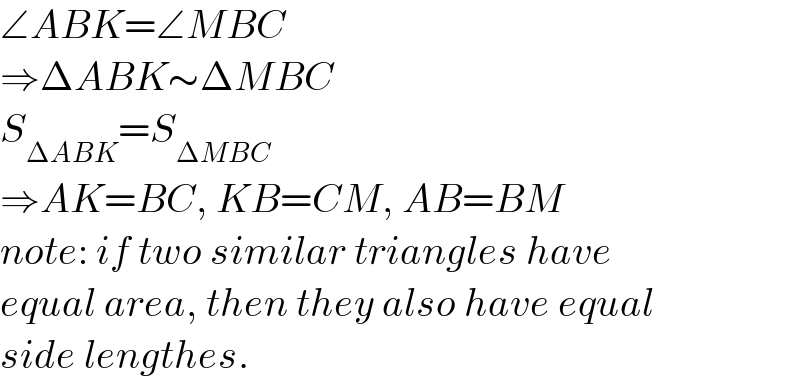
$$\angle{ABK}=\angle{MBC} \\ $$$$\Rightarrow\Delta{ABK}\sim\Delta{MBC} \\ $$$${S}_{\Delta{ABK}} ={S}_{\Delta{MBC}} \\ $$$$\Rightarrow{AK}={BC},\:{KB}={CM},\:{AB}={BM} \\ $$$${note}:\:{if}\:{two}\:{similar}\:{triangles}\:{have} \\ $$$${equal}\:{area},\:{then}\:{they}\:{also}\:{have}\:{equal} \\ $$$${side}\:{lengthes}. \\ $$
