Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

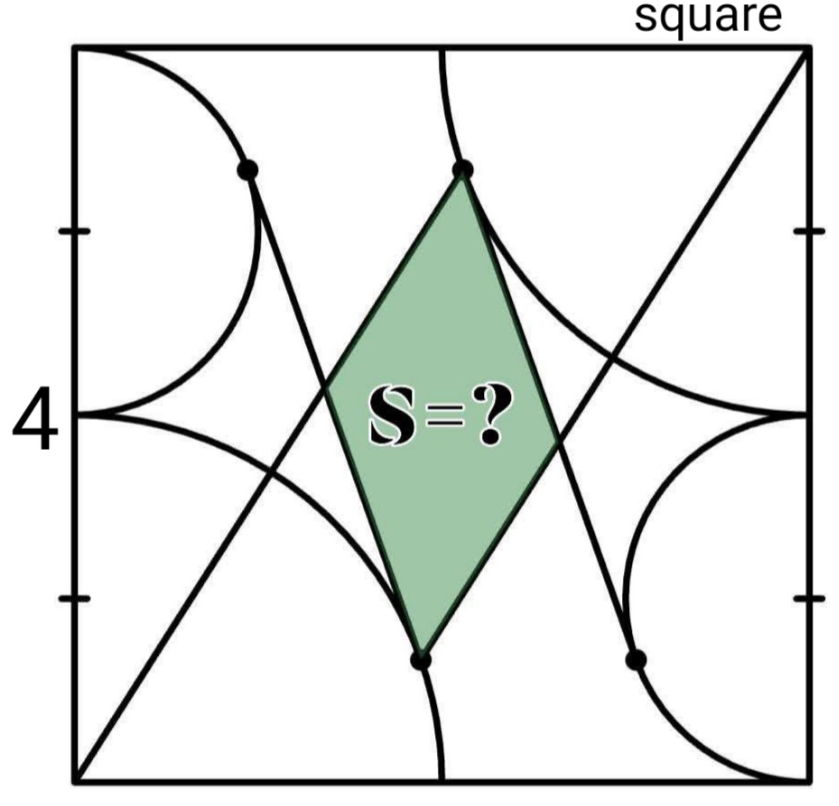
Question Number 218257 by cherokeesay last updated on 03/Apr/25

Commented by cherokeesay last updated on 03/Apr/25

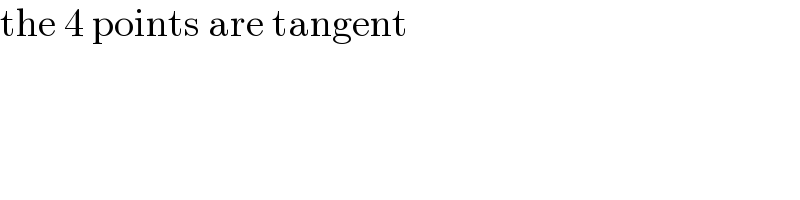
the 4 points are tangent

$$\mathrm{the}\:\mathrm{4}\:\mathrm{points}\:\mathrm{are}\:\mathrm{tangent} \\ $$

Commented by Nicholas666 last updated on 09/Apr/25

beautifull problem

$${beautifull}\:{problem} \\ $$

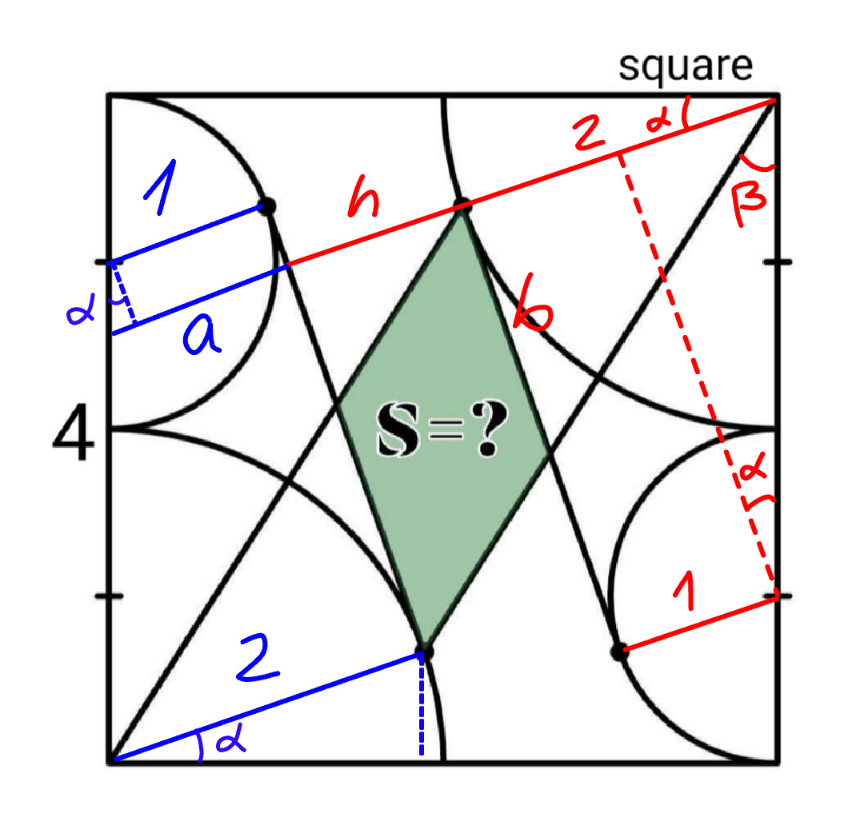
Answered by mr W last updated on 05/Apr/25

Commented by mr W last updated on 04/Apr/25

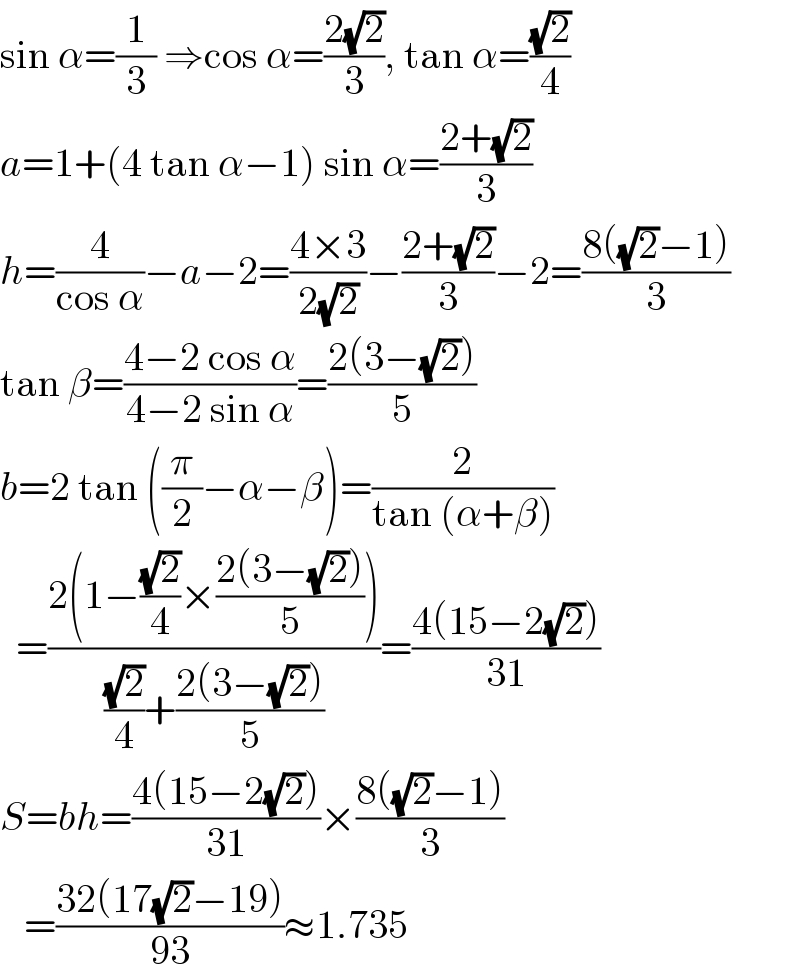
sin α=(1/3) ⇒cos α=((2(√2))/3), tan α=((√2)/4) a=1+(4 tan α−1) sin α=((2+(√2))/3) h=(4/(cos α))−a−2=((4×3)/(2(√2)))−((2+(√2))/3)−2=((8((√2)−1))/3) tan β=((4−2 cos α)/(4−2 sin α))=((2(3−(√2)))/5) b=2 tan ((π/2)−α−β)=(2/(tan (α+β))) =((2(1−((√2)/4)×((2(3−(√2)))/5)))/(((√2)/4)+((2(3−(√2)))/5)))=((4(15−2(√2)))/(31)) S=bh=((4(15−2(√2)))/(31))×((8((√2)−1))/3) =((32(17(√2)−19))/(93))≈1.735

$$\mathrm{sin}\:\alpha=\frac{\mathrm{1}}{\mathrm{3}}\:\Rightarrow\mathrm{cos}\:\alpha=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}},\:\mathrm{tan}\:\alpha=\frac{\sqrt{\mathrm{2}}}{\mathrm{4}} \\ $$$${a}=\mathrm{1}+\left(\mathrm{4}\:\mathrm{tan}\:\alpha−\mathrm{1}\right)\:\mathrm{sin}\:\alpha=\frac{\mathrm{2}+\sqrt{\mathrm{2}}}{\mathrm{3}} \\ $$$${h}=\frac{\mathrm{4}}{\mathrm{cos}\:\alpha}−{a}−\mathrm{2}=\frac{\mathrm{4}×\mathrm{3}}{\mathrm{2}\sqrt{\mathrm{2}}}−\frac{\mathrm{2}+\sqrt{\mathrm{2}}}{\mathrm{3}}−\mathrm{2}=\frac{\mathrm{8}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)}{\mathrm{3}} \\ $$$$\mathrm{tan}\:\beta=\frac{\mathrm{4}−\mathrm{2}\:\mathrm{cos}\:\alpha}{\mathrm{4}−\mathrm{2}\:\mathrm{sin}\:\alpha}=\frac{\mathrm{2}\left(\mathrm{3}−\sqrt{\mathrm{2}}\right)}{\mathrm{5}} \\ $$$${b}=\mathrm{2}\:\mathrm{tan}\:\left(\frac{\pi}{\mathrm{2}}−\alpha−\beta\right)=\frac{\mathrm{2}}{\mathrm{tan}\:\left(\alpha+\beta\right)} \\ $$$$\:\:=\frac{\mathrm{2}\left(\mathrm{1}−\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}×\frac{\mathrm{2}\left(\mathrm{3}−\sqrt{\mathrm{2}}\right)}{\mathrm{5}}\right)}{\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}+\frac{\mathrm{2}\left(\mathrm{3}−\sqrt{\mathrm{2}}\right)}{\mathrm{5}}}=\frac{\mathrm{4}\left(\mathrm{15}−\mathrm{2}\sqrt{\mathrm{2}}\right)}{\mathrm{31}} \\ $$$${S}={bh}=\frac{\mathrm{4}\left(\mathrm{15}−\mathrm{2}\sqrt{\mathrm{2}}\right)}{\mathrm{31}}×\frac{\mathrm{8}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)}{\mathrm{3}} \\ $$$$\:\:\:=\frac{\mathrm{32}\left(\mathrm{17}\sqrt{\mathrm{2}}−\mathrm{19}\right)}{\mathrm{93}}\approx\mathrm{1}.\mathrm{735} \\ $$

Commented by cherokeesay last updated on 04/Apr/25

thank you master !

$${thank}\:{you}\:{master}\:! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com