Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 218236 by mr W last updated on 02/Apr/25

Commented by mr W last updated on 02/Apr/25

why is this question deleted?

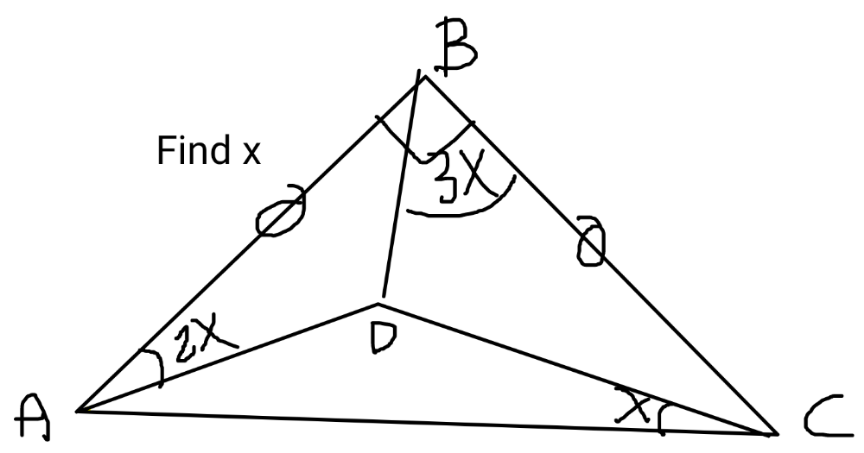
$${why}\:{is}\:{this}\:{question}\:{deleted}? \\ $$

Commented by mr W last updated on 02/Apr/25

i got x=15°

$${i}\:{got}\:{x}=\mathrm{15}° \\ $$

Commented by mr W last updated on 02/Apr/25

Answered by mr W last updated on 02/Apr/25

Commented by mr W last updated on 02/Apr/25

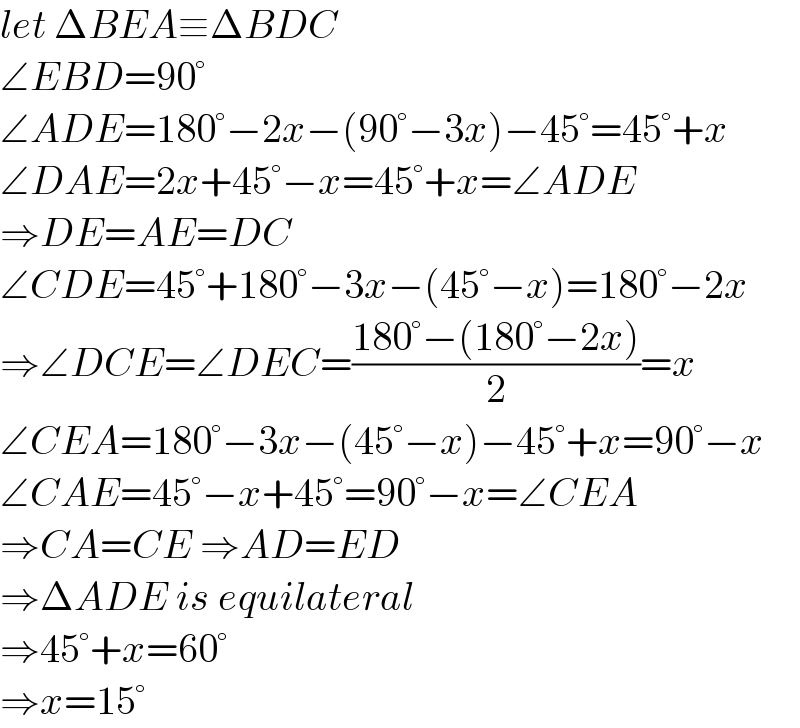
let ΔBEA≡ΔBDC ∠EBD=90° ∠ADE=180°−2x−(90°−3x)−45°=45°+x ∠DAE=2x+45°−x=45°+x=∠ADE ⇒DE=AE=DC ∠CDE=45°+180°−3x−(45°−x)=180°−2x ⇒∠DCE=∠DEC=((180°−(180°−2x))/2)=x ∠CEA=180°−3x−(45°−x)−45°+x=90°−x ∠CAE=45°−x+45°=90°−x=∠CEA ⇒CA=CE ⇒AD=ED ⇒ΔADE is equilateral ⇒45°+x=60° ⇒x=15°

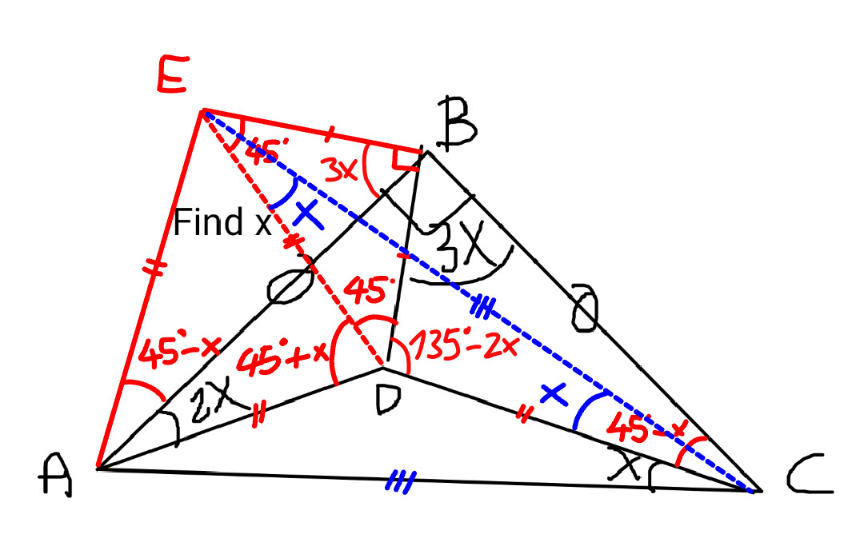
$${let}\:\Delta{BEA}\equiv\Delta{BDC} \\ $$$$\angle{EBD}=\mathrm{90}° \\ $$$$\angle{ADE}=\mathrm{180}°−\mathrm{2}{x}−\left(\mathrm{90}°−\mathrm{3}{x}\right)−\mathrm{45}°=\mathrm{45}°+{x} \\ $$$$\angle{DAE}=\mathrm{2}{x}+\mathrm{45}°−{x}=\mathrm{45}°+{x}=\angle{ADE} \\ $$$$\Rightarrow{DE}={AE}={DC} \\ $$$$\angle{CDE}=\mathrm{45}°+\mathrm{180}°−\mathrm{3}{x}−\left(\mathrm{45}°−{x}\right)=\mathrm{180}°−\mathrm{2}{x} \\ $$$$\Rightarrow\angle{DCE}=\angle{DEC}=\frac{\mathrm{180}°−\left(\mathrm{180}°−\mathrm{2}{x}\right)}{\mathrm{2}}={x} \\ $$$$\angle{CEA}=\mathrm{180}°−\mathrm{3}{x}−\left(\mathrm{45}°−{x}\right)−\mathrm{45}°+{x}=\mathrm{90}°−{x} \\ $$$$\angle{CAE}=\mathrm{45}°−{x}+\mathrm{45}°=\mathrm{90}°−{x}=\angle{CEA} \\ $$$$\Rightarrow{CA}={CE}\:\Rightarrow{AD}={ED} \\ $$$$\Rightarrow\Delta{ADE}\:{is}\:{equilateral} \\ $$$$\Rightarrow\mathrm{45}°+{x}=\mathrm{60}° \\ $$$$\Rightarrow{x}=\mathrm{15}° \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com