Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 218221 by Tawa11 last updated on 01/Apr/25

Commented by Tawa11 last updated on 01/Apr/25

Ground is rough But resistance not given how come sir.

$$ \\ $$Ground is rough But resistance not given how come sir.

Commented by mr W last updated on 02/Apr/25

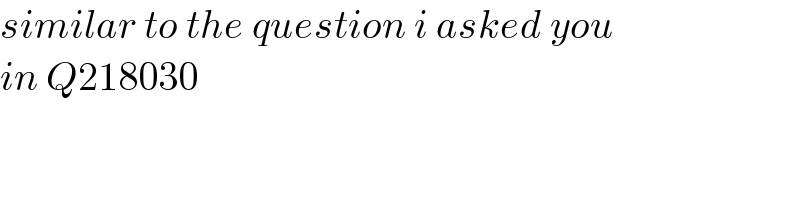
similar to the question i asked you in Q218030

$${similar}\:{to}\:{the}\:{question}\:{i}\:{asked}\:{you}\: \\ $$$${in}\:{Q}\mathrm{218030} \\ $$

Commented by mr W last updated on 02/Apr/25

acc. to that solved question what′s your answer to this question?

$${acc}.\:{to}\:{that}\:{solved}\:{question}\:{what}'{s} \\ $$$${your}\:{answer}\:{to}\:{this}\:{question}? \\ $$

Commented by Tawa11 last updated on 02/Apr/25

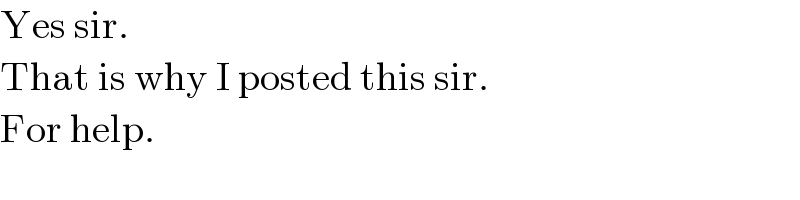
Yes sir. That is why I posted this sir. For help.

$$\mathrm{Yes}\:\mathrm{sir}. \\ $$$$\mathrm{That}\:\mathrm{is}\:\mathrm{why}\:\mathrm{I}\:\mathrm{posted}\:\mathrm{this}\:\mathrm{sir}. \\ $$$$\mathrm{For}\:\mathrm{help}. \\ $$

Commented by Tawa11 last updated on 02/Apr/25

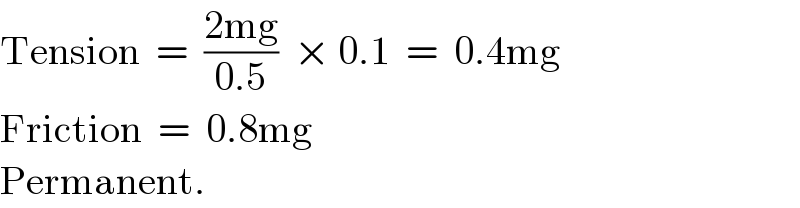
Tension = ((2mg)/(0.5)) × 0.1 = 0.4mg Friction = 0.8mg Permanent.

$$\mathrm{Tension}\:\:=\:\:\frac{\mathrm{2mg}}{\mathrm{0}.\mathrm{5}}\:\:×\:\mathrm{0}.\mathrm{1}\:\:=\:\:\mathrm{0}.\mathrm{4mg} \\ $$$$\mathrm{Friction}\:\:=\:\:\mathrm{0}.\mathrm{8mg} \\ $$$$\mathrm{Permanent}. \\ $$

Commented by mr W last updated on 02/Apr/25

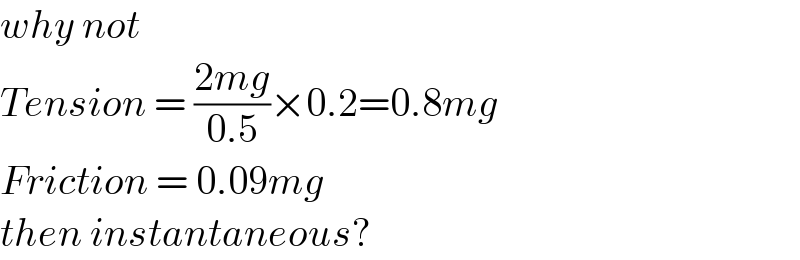
why not Tension = ((2mg)/(0.5))×0.2=0.8mg Friction = 0.09mg then instantaneous?

$${why}\:{not}\: \\ $$$${Tension}\:=\:\frac{\mathrm{2}{mg}}{\mathrm{0}.\mathrm{5}}×\mathrm{0}.\mathrm{2}=\mathrm{0}.\mathrm{8}{mg} \\ $$$${Friction}\:=\:\mathrm{0}.\mathrm{09}{mg} \\ $$$${then}\:{instantaneous}? \\ $$

Commented by mr W last updated on 03/Apr/25

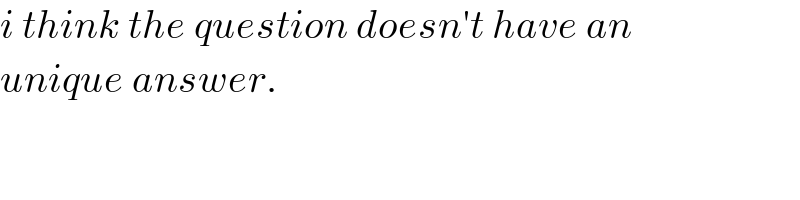
i think the question doesn′t have an unique answer.

$${i}\:{think}\:{the}\:{question}\:{doesn}'{t}\:{have}\:{an} \\ $$$${unique}\:{answer}. \\ $$

Answered by mr W last updated on 02/Apr/25

Commented by mr W last updated on 04/Apr/25

say ∣BC∣=x f=friction force (=μmg) k=(λ/l_0 )=((2mg)/l_0 ) v=1.4 m/s KE_B −PE_C =work done by friction ((mv^2 )/2)−((kx^2 )/2)=fx=μmgx ((mv^2 )/2)−((2mgx^2 )/(2l_0 ))=μmgx (x^2 /l_0 )+μx−(v^2 /(2g))=0 ⇒x=(−μ+(√(μ^2 +((2v^2 )/(gl_0 )))))(l_0 /2) tension in string T=kx=((2mg)/l_0 )×(−μ+(√(μ^2 +((2v^2 )/(gl_0 )))))(l_0 /2) =(−μ+(√(μ^2 +((2v^2 )/(gl_0 )))))mg if T>f, particle will move further. if T≤f, particle rests permanently. T−f=(−2μ+(√(μ^2 +((2v^2 )/(gl_0 )))))mg −2μ+(√(μ^2 +((2v^2 )/(gl_0 ))))=0 ⇒μ=(√((2v^2 )/(3gl_0 )))=(√((2×1.4^2 )/(3×9.81×0.5)))≈0.516 if μ<0.516, position of rest is instantaneous. if μ≥0.516, position of rest is permanent. since μ is unknown in question, we can not uniquely determine if the position of rest is permanent or instantaneous.

$${say}\:\mid{BC}\mid={x} \\ $$$${f}={friction}\:{force}\:\left(=\mu{mg}\right) \\ $$$${k}=\frac{\lambda}{{l}_{\mathrm{0}} }=\frac{\mathrm{2}{mg}}{{l}_{\mathrm{0}} } \\ $$$${v}=\mathrm{1}.\mathrm{4}\:{m}/{s} \\ $$$${KE}_{{B}} −{PE}_{{C}} ={work}\:{done}\:{by}\:{friction} \\ $$$$\frac{{mv}^{\mathrm{2}} }{\mathrm{2}}−\frac{{kx}^{\mathrm{2}} }{\mathrm{2}}={fx}=\mu{mgx} \\ $$$$\frac{{mv}^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{2}{mgx}^{\mathrm{2}} }{\mathrm{2}{l}_{\mathrm{0}} }=\mu{mgx} \\ $$$$\frac{{x}^{\mathrm{2}} }{{l}_{\mathrm{0}} }+\mu{x}−\frac{{v}^{\mathrm{2}} }{\mathrm{2}{g}}=\mathrm{0} \\ $$$$\Rightarrow{x}=\left(−\mu+\sqrt{\mu^{\mathrm{2}} +\frac{\mathrm{2}{v}^{\mathrm{2}} }{{gl}_{\mathrm{0}} }}\right)\frac{{l}_{\mathrm{0}} }{\mathrm{2}} \\ $$$${tension}\:{in}\:{string} \\ $$$${T}={kx}=\frac{\mathrm{2}{mg}}{{l}_{\mathrm{0}} }×\left(−\mu+\sqrt{\mu^{\mathrm{2}} +\frac{\mathrm{2}{v}^{\mathrm{2}} }{{gl}_{\mathrm{0}} }}\right)\frac{{l}_{\mathrm{0}} }{\mathrm{2}} \\ $$$$\:\:\:=\left(−\mu+\sqrt{\mu^{\mathrm{2}} +\frac{\mathrm{2}{v}^{\mathrm{2}} }{{gl}_{\mathrm{0}} }}\right){mg} \\ $$$${if}\:{T}>{f},\:{particle}\:{will}\:{move}\:{further}. \\ $$$${if}\:{T}\leqslant{f},\:{particle}\:{rests}\:{permanently}. \\ $$$${T}−{f}=\left(−\mathrm{2}\mu+\sqrt{\mu^{\mathrm{2}} +\frac{\mathrm{2}{v}^{\mathrm{2}} }{{gl}_{\mathrm{0}} }}\right){mg} \\ $$$$−\mathrm{2}\mu+\sqrt{\mu^{\mathrm{2}} +\frac{\mathrm{2}{v}^{\mathrm{2}} }{{gl}_{\mathrm{0}} }}=\mathrm{0} \\ $$$$\Rightarrow\mu=\sqrt{\frac{\mathrm{2}{v}^{\mathrm{2}} }{\mathrm{3}{gl}_{\mathrm{0}} }}=\sqrt{\frac{\mathrm{2}×\mathrm{1}.\mathrm{4}^{\mathrm{2}} }{\mathrm{3}×\mathrm{9}.\mathrm{81}×\mathrm{0}.\mathrm{5}}}\approx\mathrm{0}.\mathrm{516} \\ $$$${if}\:\mu<\mathrm{0}.\mathrm{516},\:{position}\:{of}\:{rest}\:{is}\: \\ $$$${instantaneous}.\:{if}\:\mu\geqslant\mathrm{0}.\mathrm{516},\:{position} \\ $$$${of}\:{rest}\:{is}\:{permanent}. \\ $$$$ \\ $$$${since}\:\mu\:{is}\:{unknown}\:{in}\:{question}, \\ $$$${we}\:{can}\:{not}\:{uniquely}\:{determine}\:{if} \\ $$$${the}\:{position}\:{of}\:{rest}\:{is}\:{permanent} \\ $$$${or}\:{instantaneous}. \\ $$

Commented by Tawa11 last updated on 02/Apr/25

Commented by Tawa11 last updated on 02/Apr/25

Sir, see ∣BC∣ = 0.1. Is this approach correct?. This will tally with your working sir. If ∣BC∣ ≤ 0.13m it is permanent.

$$\mathrm{Sir},\:\mathrm{see}\:\mid\mathrm{BC}\mid\:=\:\mathrm{0}.\mathrm{1}. \\ $$$$\mathrm{Is}\:\mathrm{this}\:\mathrm{approach}\:\mathrm{correct}?. \\ $$$$\mathrm{This}\:\mathrm{will}\:\mathrm{tally}\:\mathrm{with}\:\mathrm{your}\:\mathrm{working}\:\mathrm{sir}. \\ $$$$\mathrm{If}\:\mid\mathrm{BC}\mid\:\leqslant\:\mathrm{0}.\mathrm{13m}\:\:\:\mathrm{it}\:\mathrm{is}\:\mathrm{permanent}. \\ $$

Commented by mr W last updated on 03/Apr/25

i asked you what you got, but you answered me what an other person did and you are not sure if he or she is right. i have showed my complete working with all steps which you can follow and check to make your own judge. as i have said with given conditions the question doesn′t have an unique answer. i have showed why. in the solution you presented above a friction coefficient μ=0.8 is taken, but this is not given in the original question. in this case how can i answer you if the approach is correct? why didn′t he/she take μ=0.1? then he/she would have got a totally different result and say that the stop is instantaneous.

$${i}\:{asked}\:{you}\:{what}\:{you}\:{got},\:{but}\:{you} \\ $$$${answered}\:{me}\:{what}\:{an}\:{other}\:{person} \\ $$$${did}\:{and}\:{you}\:{are}\:{not}\:{sure}\:{if}\:{he} \\ $$$${or}\:{she}\:{is}\:{right}.\:{i}\:{have}\:{showed}\:{my} \\ $$$${complete}\:{working}\:{with}\:{all}\:{steps} \\ $$$${which}\:{you}\:{can}\:{follow}\:{and}\:{check}\:{to} \\ $$$${make}\:{your}\:{own}\:{judge}. \\ $$$${as}\:{i}\:{have}\:{said}\:{with}\:{given}\:{conditions} \\ $$$${the}\:{question}\:{doesn}'{t}\:{have}\:{an}\:{unique} \\ $$$${answer}.\:{i}\:{have}\:{showed}\:{why}. \\ $$$${in}\:{the}\:{solution}\:{you}\:{presented}\:{above} \\ $$$${a}\:{friction}\:{coefficient}\:\mu=\mathrm{0}.\mathrm{8}\:{is} \\ $$$${taken},\:{but}\:\underline{{this}\:{is}\:{not}\:{given}\:{in}\:{the}} \\ $$$$\underline{{original}\:{question}}.\:{in}\:{this}\:{case}\:{how} \\ $$$${can}\:{i}\:{answer}\:{you}\:{if}\:{the}\:{approach}\: \\ $$$${is}\:{correct}?\:{why}\:{didn}'{t}\:{he}/{she}\:{take}\: \\ $$$$\mu=\mathrm{0}.\mathrm{1}?\:{then}\:{he}/{she}\:{would}\:{have}\: \\ $$$${got}\:{a}\:{totally}\:{different}\:{result}\:{and}\: \\ $$$${say}\:{that}\:{the}\:{stop}\:{is}\:{instantaneous}. \\ $$

Commented by Tawa11 last updated on 03/Apr/25

Sir, I am only showing you sir. After I see your solution. I see the mistake I also made. I followed their concept before. But I understand your point sir. And I asked the question because I doubt their workings. I just need to show you that you are right since I have their duplicate workings. I only doubt their workings. Thanks for your time sir

$$\mathrm{Sir}, \\ $$$$\mathrm{I}\:\mathrm{am}\:\mathrm{only}\:\mathrm{showing}\:\mathrm{you}\:\mathrm{sir}. \\ $$$$\mathrm{After}\:\mathrm{I}\:\mathrm{see}\:\mathrm{your}\:\mathrm{solution}. \\ $$$$\mathrm{I}\:\mathrm{see}\:\mathrm{the}\:\mathrm{mistake}\:\mathrm{I}\:\mathrm{also}\:\mathrm{made}. \\ $$$$\mathrm{I}\:\mathrm{followed}\:\mathrm{their}\:\mathrm{concept}\:\mathrm{before}. \\ $$$$\mathrm{But}\:\mathrm{I}\:\mathrm{understand}\:\mathrm{your}\:\mathrm{point}\:\mathrm{sir}. \\ $$$$\mathrm{And}\:\mathrm{I}\:\mathrm{asked}\:\mathrm{the}\:\mathrm{question}\:\mathrm{because} \\ $$$$\mathrm{I}\:\mathrm{doubt}\:\mathrm{their}\:\mathrm{workings}. \\ $$$$ \\ $$$$\mathrm{I}\:\mathrm{just}\:\mathrm{need}\:\mathrm{to}\:\mathrm{show}\:\mathrm{you}\:\mathrm{that}\:\mathrm{you}\:\mathrm{are} \\ $$$$\mathrm{right}\:\mathrm{since}\:\mathrm{I}\:\mathrm{have}\:\mathrm{their}\:\mathrm{duplicate}\:\mathrm{workings}. \\ $$$$\mathrm{I}\:\mathrm{only}\:\mathrm{doubt}\:\mathrm{their}\:\mathrm{workings}. \\ $$$$ \\ $$$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir} \\ $$

Commented by mr W last updated on 03/Apr/25

ok. now you know that the problem lies in the question itself.

$${ok}.\:{now}\:{you}\:{know}\:{that}\:{the}\:{problem} \\ $$$${lies}\:{in}\:{the}\:{question}\:{itself}. \\ $$

Commented by Tawa11 last updated on 03/Apr/25

Yes sir. Clearly seen.

$$\mathrm{Yes}\:\mathrm{sir}.\:\mathrm{Clearly}\:\mathrm{seen}. \\ $$

Commented by Tawa11 last updated on 03/Apr/25

God bless you more sir.

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{more}\:\mathrm{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com