
Question Number 218115 by Hanuda354 last updated on 29/Mar/25
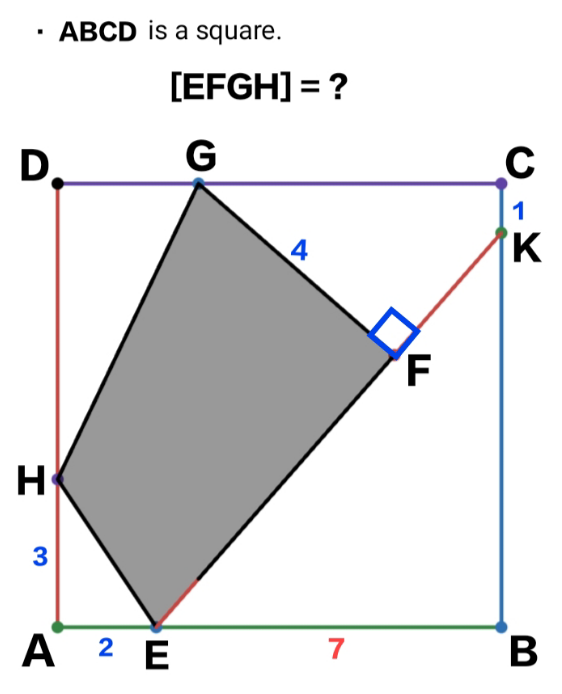
Answered by mr W last updated on 30/Mar/25
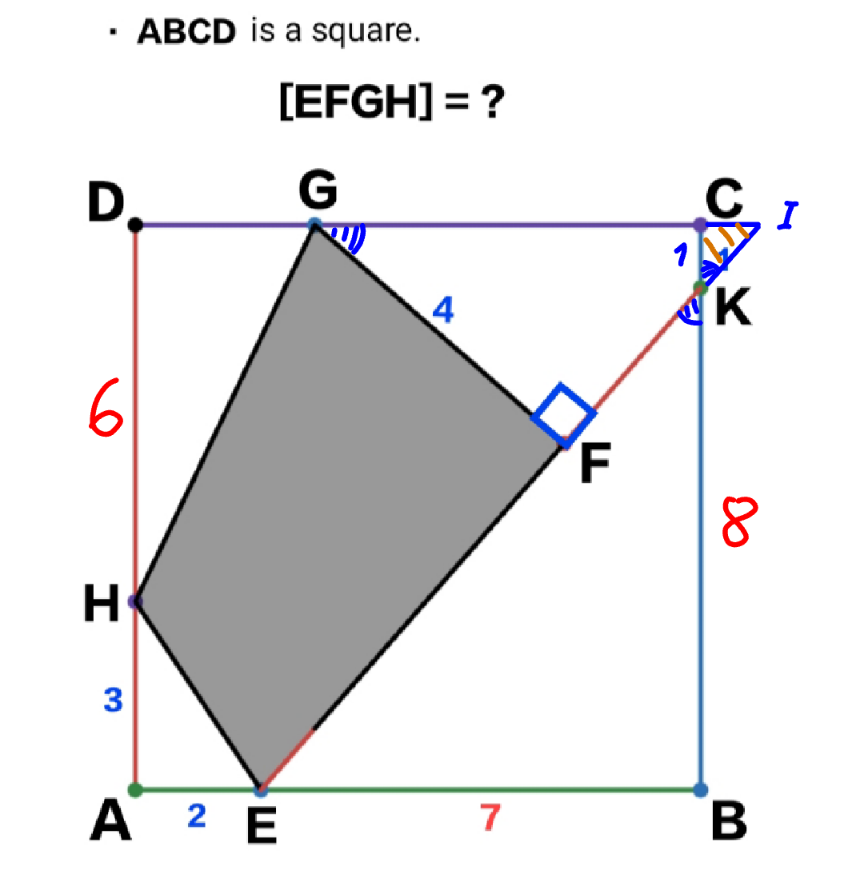
Commented by mr W last updated on 30/Mar/25
![EK=(√(7^2 +8^2 ))=(√(113)) CI=((1×7)/8)=(7/8) GI=((4×(√(113)))/8)=((√(113))/2) DG=9+(7/8)−((√(113))/2)=((79)/8)−((√(113))/2) [EFGH]=9^2 −((2×3)/2)−(6/2)×(((79)/8)−((√(113))/2))−((7×8)/2)×(1+(1/2^2 )−(1/8^2 )) =((221)/(16))+((3(√(113)))/2)≈29.76](Q218122.png)
$${EK}=\sqrt{\mathrm{7}^{\mathrm{2}} +\mathrm{8}^{\mathrm{2}} }=\sqrt{\mathrm{113}} \\ $$$${CI}=\frac{\mathrm{1}×\mathrm{7}}{\mathrm{8}}=\frac{\mathrm{7}}{\mathrm{8}} \\ $$$${GI}=\frac{\mathrm{4}×\sqrt{\mathrm{113}}}{\mathrm{8}}=\frac{\sqrt{\mathrm{113}}}{\mathrm{2}} \\ $$$${DG}=\mathrm{9}+\frac{\mathrm{7}}{\mathrm{8}}−\frac{\sqrt{\mathrm{113}}}{\mathrm{2}}=\frac{\mathrm{79}}{\mathrm{8}}−\frac{\sqrt{\mathrm{113}}}{\mathrm{2}} \\ $$$$\left[{EFGH}\right]=\mathrm{9}^{\mathrm{2}} −\frac{\mathrm{2}×\mathrm{3}}{\mathrm{2}}−\frac{\mathrm{6}}{\mathrm{2}}×\left(\frac{\mathrm{79}}{\mathrm{8}}−\frac{\sqrt{\mathrm{113}}}{\mathrm{2}}\right)−\frac{\mathrm{7}×\mathrm{8}}{\mathrm{2}}×\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{8}^{\mathrm{2}} }\right) \\ $$$$\:\:\:\:\:\:\:\:=\frac{\mathrm{221}}{\mathrm{16}}+\frac{\mathrm{3}\sqrt{\mathrm{113}}}{\mathrm{2}}\approx\mathrm{29}.\mathrm{76}\: \\ $$
Commented by Hanuda354 last updated on 30/Mar/25

$$\mathrm{Thank}\:\mathrm{you},\:\mathrm{sir}. \\ $$
