
Question Number 218030 by Tawa11 last updated on 26/Mar/25

Commented by mr W last updated on 26/Mar/25
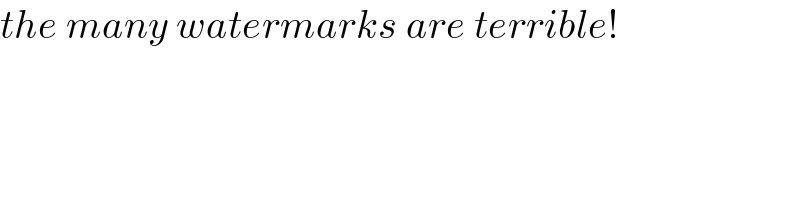
$${the}\:{many}\:{watermarks}\:{are}\:{terrible}! \\ $$
Commented by mr W last updated on 26/Mar/25

$${see}\:{Q}\mathrm{216110} \\ $$
Commented by Tawa11 last updated on 26/Mar/25

$$\mathrm{Done}\:\mathrm{sir}. \\ $$$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$$$\mathrm{I}\:\mathrm{appreciate}. \\ $$
Commented by mr W last updated on 26/Mar/25
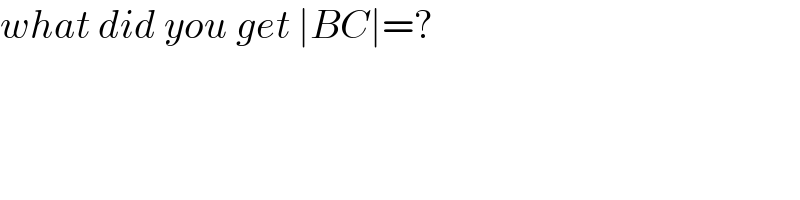
$${what}\:{did}\:{you}\:{get}\:\mid{BC}\mid=? \\ $$
Commented by Tawa11 last updated on 26/Mar/25

$$\mathrm{0}.\mathrm{4m}\:\:\mathrm{sir} \\ $$
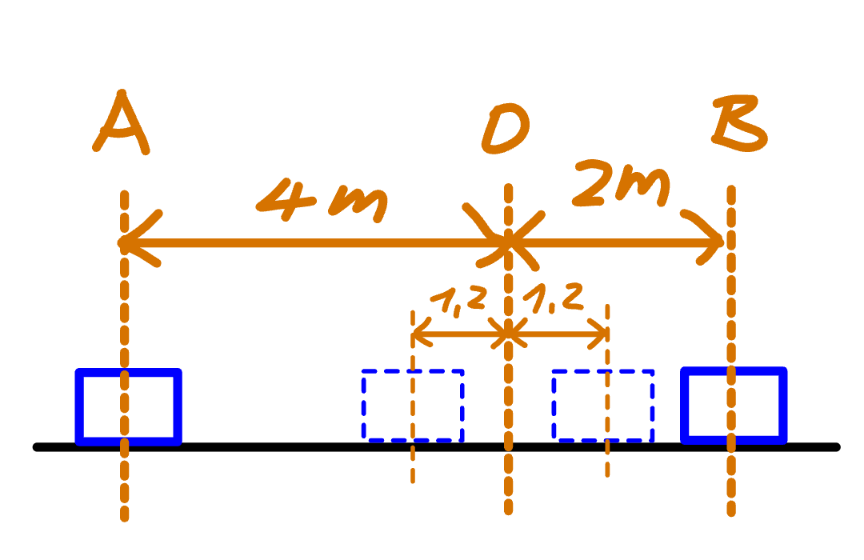
Answered by mr W last updated on 02/Apr/25
Commented by Tawa11 last updated on 02/Apr/25

$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$$$\mathrm{I}\:\mathrm{appreciate}. \\ $$
Commented by mr W last updated on 02/Apr/25
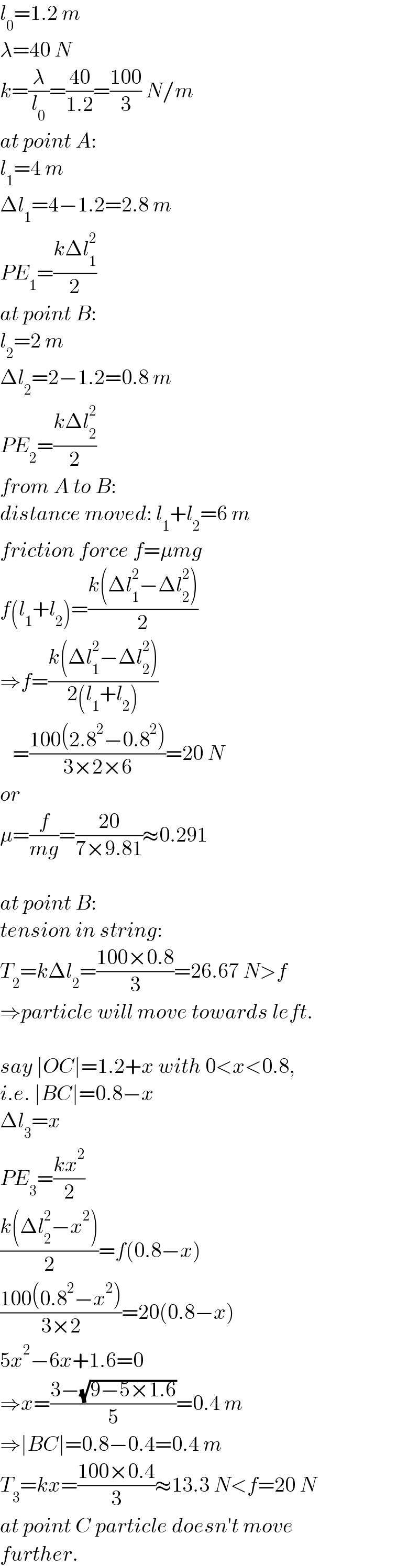
$${l}_{\mathrm{0}} =\mathrm{1}.\mathrm{2}\:{m} \\ $$$$\lambda=\mathrm{40}\:{N} \\ $$$${k}=\frac{\lambda}{{l}_{\mathrm{0}} }=\frac{\mathrm{40}}{\mathrm{1}.\mathrm{2}}=\frac{\mathrm{100}}{\mathrm{3}}\:{N}/{m} \\ $$$${at}\:{point}\:{A}: \\ $$$${l}_{\mathrm{1}} =\mathrm{4}\:{m} \\ $$$$\Delta{l}_{\mathrm{1}} =\mathrm{4}−\mathrm{1}.\mathrm{2}=\mathrm{2}.\mathrm{8}\:{m} \\ $$$${PE}_{\mathrm{1}} =\frac{{k}\Delta{l}_{\mathrm{1}} ^{\mathrm{2}} }{\mathrm{2}} \\ $$$${at}\:{point}\:{B}: \\ $$$${l}_{\mathrm{2}} =\mathrm{2}\:{m} \\ $$$$\Delta{l}_{\mathrm{2}} =\mathrm{2}−\mathrm{1}.\mathrm{2}=\mathrm{0}.\mathrm{8}\:{m} \\ $$$${PE}_{\mathrm{2}} =\frac{{k}\Delta{l}_{\mathrm{2}} ^{\mathrm{2}} }{\mathrm{2}} \\ $$$${from}\:{A}\:{to}\:{B}: \\ $$$${distance}\:{moved}:\:{l}_{\mathrm{1}} +{l}_{\mathrm{2}} =\mathrm{6}\:{m} \\ $$$${friction}\:{force}\:{f}=\mu{mg} \\ $$$${f}\left({l}_{\mathrm{1}} +{l}_{\mathrm{2}} \right)=\frac{{k}\left(\Delta{l}_{\mathrm{1}} ^{\mathrm{2}} −\Delta{l}_{\mathrm{2}} ^{\mathrm{2}} \right)}{\mathrm{2}} \\ $$$$\Rightarrow{f}=\frac{{k}\left(\Delta{l}_{\mathrm{1}} ^{\mathrm{2}} −\Delta{l}_{\mathrm{2}} ^{\mathrm{2}} \right)}{\mathrm{2}\left({l}_{\mathrm{1}} +{l}_{\mathrm{2}} \right)} \\ $$$$\:\:\:=\frac{\mathrm{100}\left(\mathrm{2}.\mathrm{8}^{\mathrm{2}} −\mathrm{0}.\mathrm{8}^{\mathrm{2}} \right)}{\mathrm{3}×\mathrm{2}×\mathrm{6}}=\mathrm{20}\:{N} \\ $$$${or} \\ $$$$\mu=\frac{{f}}{{mg}}=\frac{\mathrm{20}}{\mathrm{7}×\mathrm{9}.\mathrm{81}}\approx\mathrm{0}.\mathrm{291} \\ $$$$ \\ $$$${at}\:{point}\:{B}: \\ $$$${tension}\:{in}\:{string}: \\ $$$${T}_{\mathrm{2}} ={k}\Delta{l}_{\mathrm{2}} =\frac{\mathrm{100}×\mathrm{0}.\mathrm{8}}{\mathrm{3}}=\mathrm{26}.\mathrm{67}\:{N}>{f} \\ $$$$\Rightarrow{particle}\:{will}\:{move}\:{towards}\:{left}. \\ $$$$ \\ $$$${say}\:\mid{OC}\mid=\mathrm{1}.\mathrm{2}+{x}\:{with}\:\mathrm{0}<{x}<\mathrm{0}.\mathrm{8},\: \\ $$$${i}.{e}.\:\mid{BC}\mid=\mathrm{0}.\mathrm{8}−{x} \\ $$$$\Delta{l}_{\mathrm{3}} ={x} \\ $$$${PE}_{\mathrm{3}} =\frac{{kx}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\frac{{k}\left(\Delta{l}_{\mathrm{2}} ^{\mathrm{2}} −{x}^{\mathrm{2}} \right)}{\mathrm{2}}={f}\left(\mathrm{0}.\mathrm{8}−{x}\right) \\ $$$$\frac{\mathrm{100}\left(\mathrm{0}.\mathrm{8}^{\mathrm{2}} −{x}^{\mathrm{2}} \right)}{\mathrm{3}×\mathrm{2}}=\mathrm{20}\left(\mathrm{0}.\mathrm{8}−{x}\right) \\ $$$$\mathrm{5}{x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{1}.\mathrm{6}=\mathrm{0} \\ $$$$\Rightarrow{x}=\frac{\mathrm{3}−\sqrt{\mathrm{9}−\mathrm{5}×\mathrm{1}.\mathrm{6}}}{\mathrm{5}}=\mathrm{0}.\mathrm{4}\:{m}\: \\ $$$$\Rightarrow\mid{BC}\mid=\mathrm{0}.\mathrm{8}−\mathrm{0}.\mathrm{4}=\mathrm{0}.\mathrm{4}\:{m} \\ $$$${T}_{\mathrm{3}} ={kx}=\frac{\mathrm{100}×\mathrm{0}.\mathrm{4}}{\mathrm{3}}\approx\mathrm{13}.\mathrm{3}\:{N}<{f}=\mathrm{20}\:{N} \\ $$$${at}\:{point}\:{C}\:{particle}\:{doesn}'{t}\:{move} \\ $$$${further}. \\ $$
