
Question Number 218021 by mnjuly1970 last updated on 26/Mar/25
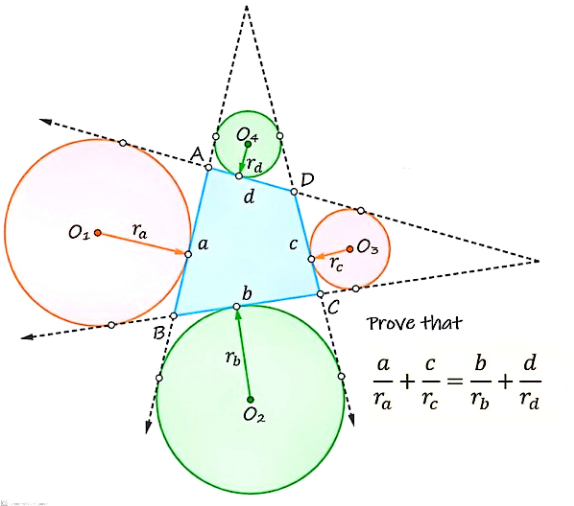
Answered by mr W last updated on 27/Mar/25
Commented by mr W last updated on 27/Mar/25
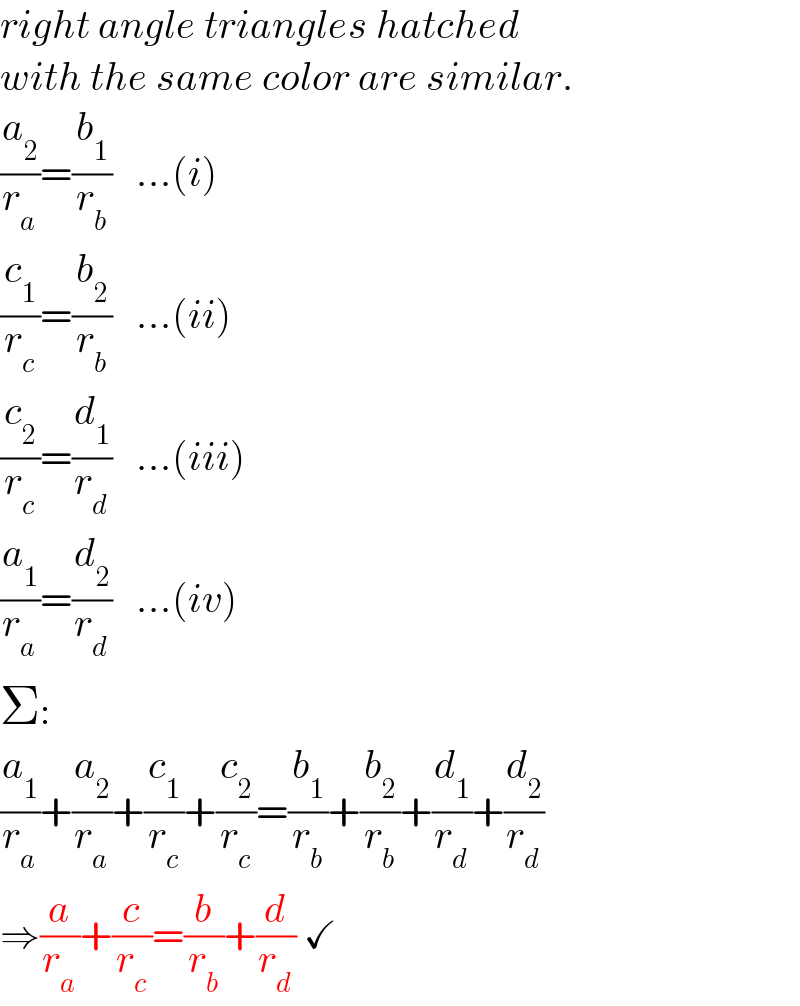
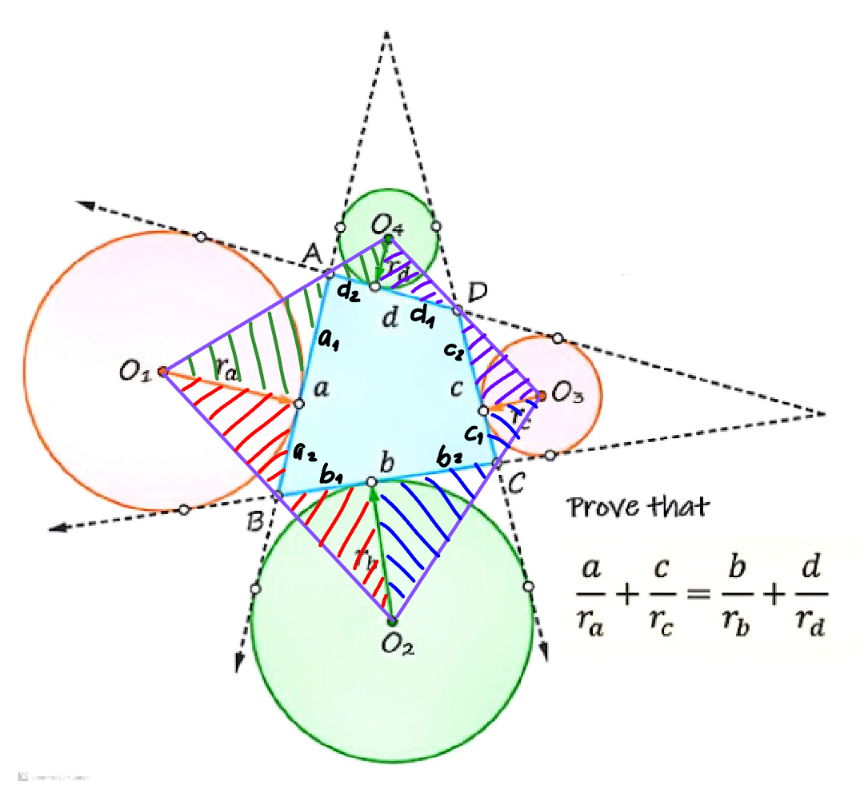
$${right}\:{angle}\:{triangles}\:{hatched} \\ $$$${with}\:{the}\:{same}\:{color}\:{are}\:{similar}. \\ $$$$\frac{{a}_{\mathrm{2}} }{{r}_{{a}} }=\frac{{b}_{\mathrm{1}} }{{r}_{{b}} }\:\:\:...\left({i}\right) \\ $$$$\frac{{c}_{\mathrm{1}} }{{r}_{{c}} }=\frac{{b}_{\mathrm{2}} }{{r}_{{b}} }\:\:\:...\left({ii}\right) \\ $$$$\frac{{c}_{\mathrm{2}} }{{r}_{{c}} }=\frac{{d}_{\mathrm{1}} }{{r}_{{d}} }\:\:\:...\left({iii}\right) \\ $$$$\frac{{a}_{\mathrm{1}} }{{r}_{{a}} }=\frac{{d}_{\mathrm{2}} }{{r}_{{d}} }\:\:\:...\left({iv}\right) \\ $$$$\Sigma: \\ $$$$\frac{{a}_{\mathrm{1}} }{{r}_{{a}} }+\frac{{a}_{\mathrm{2}} }{{r}_{{a}} }+\frac{{c}_{\mathrm{1}} }{{r}_{{c}} }+\frac{{c}_{\mathrm{2}} }{{r}_{{c}} }=\frac{{b}_{\mathrm{1}} }{{r}_{{b}} }+\frac{{b}_{\mathrm{2}} }{{r}_{{b}} }+\frac{{d}_{\mathrm{1}} }{{r}_{{d}} }+\frac{{d}_{\mathrm{2}} }{{r}_{{d}} } \\ $$$$\Rightarrow\frac{{a}}{{r}_{{a}} }+\frac{{c}}{{r}_{{c}} }=\frac{{b}}{{r}_{{b}} }+\frac{{d}}{{r}_{{d}} }\:\checkmark \\ $$
Commented by mnjuly1970 last updated on 27/Mar/25
$${thank}\:{you}\:{so}\:{much}\:{sir}\:{W} \\ $$
