Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 218013 by Tawa11 last updated on 25/Mar/25

Answered by mr W last updated on 26/Mar/25

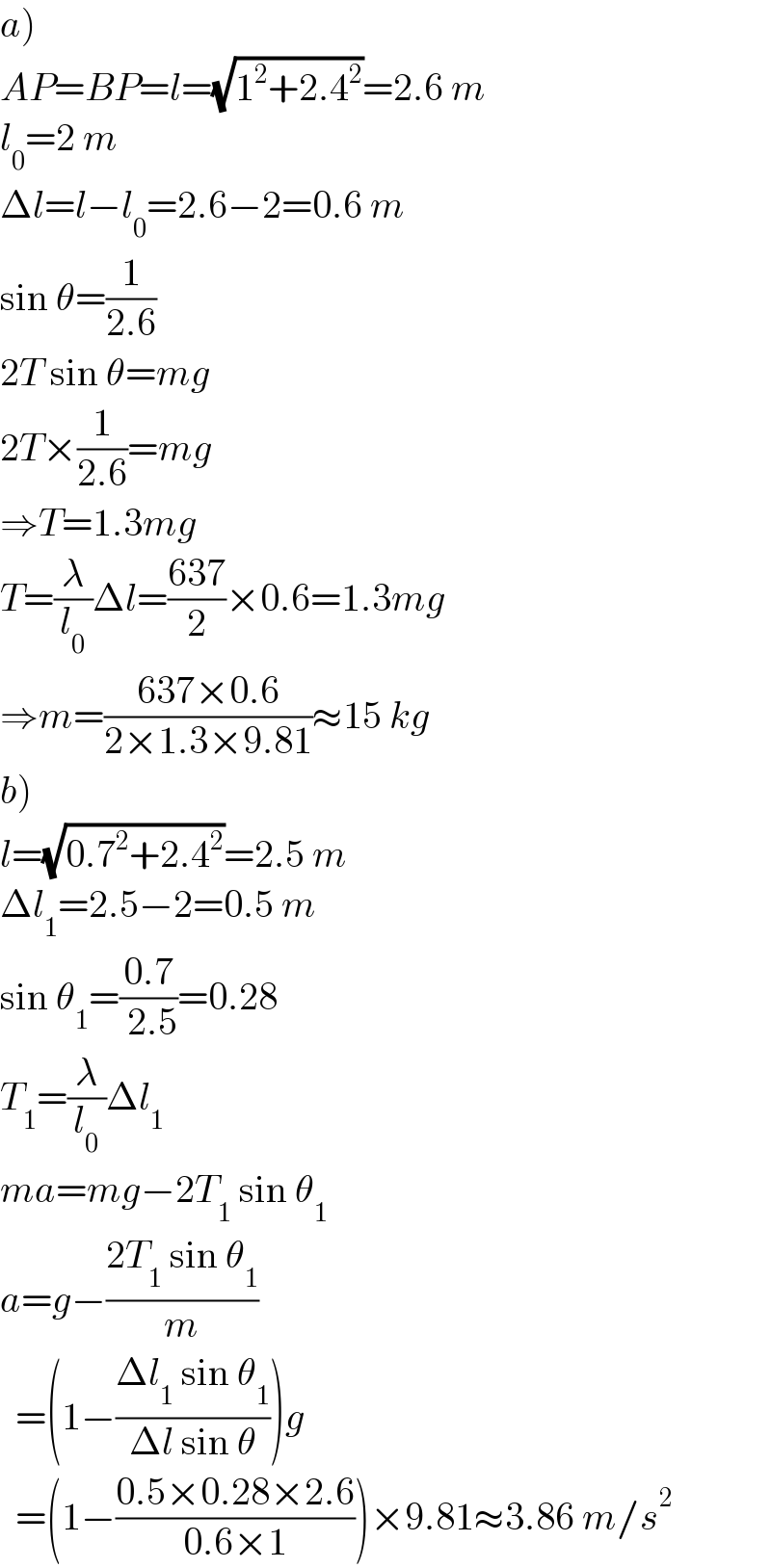
a) AP=BP=l=(√(1^2 +2.4^2 ))=2.6 m l_0 =2 m Δl=l−l_0 =2.6−2=0.6 m sin θ=(1/(2.6)) 2T sin θ=mg 2T×(1/(2.6))=mg ⇒T=1.3mg T=(λ/l_0 )Δl=((637)/2)×0.6=1.3mg ⇒m=((637×0.6)/(2×1.3×9.81))≈15 kg b) l=(√(0.7^2 +2.4^2 ))=2.5 m Δl_1 =2.5−2=0.5 m sin θ_1 =((0.7)/( 2.5))=0.28 T_1 =(λ/l_0 )Δl_1 ma=mg−2T_1 sin θ_1 a=g−((2T_1 sin θ_1 )/m) =(1−((Δl_1 sin θ_1 )/(Δl sin θ)))g =(1−((0.5×0.28×2.6)/(0.6×1)))×9.81≈3.86 m/s^2

$$\left.{a}\right) \\ $$$${AP}={BP}={l}=\sqrt{\mathrm{1}^{\mathrm{2}} +\mathrm{2}.\mathrm{4}^{\mathrm{2}} }=\mathrm{2}.\mathrm{6}\:{m} \\ $$$${l}_{\mathrm{0}} =\mathrm{2}\:{m} \\ $$$$\Delta{l}={l}−{l}_{\mathrm{0}} =\mathrm{2}.\mathrm{6}−\mathrm{2}=\mathrm{0}.\mathrm{6}\:{m} \\ $$$$\mathrm{sin}\:\theta=\frac{\mathrm{1}}{\mathrm{2}.\mathrm{6}} \\ $$$$\mathrm{2}{T}\:\mathrm{sin}\:\theta={mg} \\ $$$$\mathrm{2}{T}×\frac{\mathrm{1}}{\mathrm{2}.\mathrm{6}}={mg} \\ $$$$\Rightarrow{T}=\mathrm{1}.\mathrm{3}{mg} \\ $$$${T}=\frac{\lambda}{{l}_{\mathrm{0}} }\Delta{l}=\frac{\mathrm{637}}{\mathrm{2}}×\mathrm{0}.\mathrm{6}=\mathrm{1}.\mathrm{3}{mg} \\ $$$$\Rightarrow{m}=\frac{\mathrm{637}×\mathrm{0}.\mathrm{6}}{\mathrm{2}×\mathrm{1}.\mathrm{3}×\mathrm{9}.\mathrm{81}}\approx\mathrm{15}\:{kg} \\ $$$$\left.{b}\right) \\ $$$${l}=\sqrt{\mathrm{0}.\mathrm{7}^{\mathrm{2}} +\mathrm{2}.\mathrm{4}^{\mathrm{2}} }=\mathrm{2}.\mathrm{5}\:{m} \\ $$$$\Delta{l}_{\mathrm{1}} =\mathrm{2}.\mathrm{5}−\mathrm{2}=\mathrm{0}.\mathrm{5}\:{m} \\ $$$$\mathrm{sin}\:\theta_{\mathrm{1}} =\frac{\mathrm{0}.\mathrm{7}}{\:\mathrm{2}.\mathrm{5}}=\mathrm{0}.\mathrm{28} \\ $$$${T}_{\mathrm{1}} =\frac{\lambda}{{l}_{\mathrm{0}} }\Delta{l}_{\mathrm{1}} \\ $$$${ma}={mg}−\mathrm{2}{T}_{\mathrm{1}} \:\mathrm{sin}\:\theta_{\mathrm{1}} \\ $$$${a}={g}−\frac{\mathrm{2}{T}_{\mathrm{1}} \:\mathrm{sin}\:\theta_{\mathrm{1}} }{{m}} \\ $$$$\:\:=\left(\mathrm{1}−\frac{\Delta{l}_{\mathrm{1}} \:\mathrm{sin}\:\theta_{\mathrm{1}} }{\Delta{l}\:\mathrm{sin}\:\theta}\right){g} \\ $$$$\:\:=\left(\mathrm{1}−\frac{\mathrm{0}.\mathrm{5}×\mathrm{0}.\mathrm{28}×\mathrm{2}.\mathrm{6}}{\mathrm{0}.\mathrm{6}×\mathrm{1}}\right)×\mathrm{9}.\mathrm{81}\approx\mathrm{3}.\mathrm{86}\:{m}/{s}^{\mathrm{2}} \\ $$

Commented by Tawa11 last updated on 26/Mar/25

Thanks sir. I appreciate.

$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$$$\mathrm{I}\:\mathrm{appreciate}. \\ $$

Commented by Tawa11 last updated on 26/Mar/25

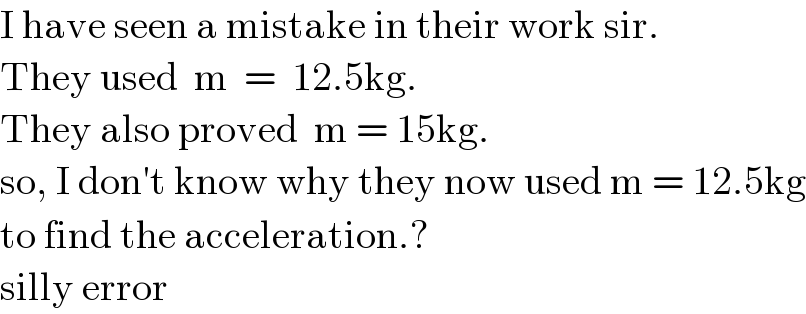
I have seen a mistake in their work sir. They used m = 12.5kg. They also proved m = 15kg. so, I don′t know why they now used m = 12.5kg to find the acceleration.? silly error

$$\mathrm{I}\:\mathrm{have}\:\mathrm{seen}\:\mathrm{a}\:\mathrm{mistake}\:\mathrm{in}\:\mathrm{their}\:\mathrm{work}\:\mathrm{sir}. \\ $$$$\mathrm{They}\:\mathrm{used}\:\:\mathrm{m}\:\:=\:\:\mathrm{12}.\mathrm{5kg}. \\ $$$$\mathrm{They}\:\mathrm{also}\:\mathrm{proved}\:\:\mathrm{m}\:=\:\mathrm{15kg}. \\ $$$$\mathrm{so},\:\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{know}\:\mathrm{why}\:\mathrm{they}\:\mathrm{now}\:\mathrm{used}\:\mathrm{m}\:=\:\mathrm{12}.\mathrm{5kg} \\ $$$$\mathrm{to}\:\mathrm{find}\:\mathrm{the}\:\mathrm{acceleration}.? \\ $$$$\mathrm{silly}\:\mathrm{error} \\ $$

Commented by Tawa11 last updated on 26/Mar/25

Commented by mr W last updated on 26/Mar/25

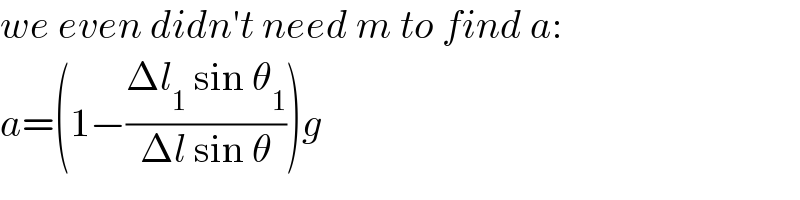
we even didn′t need m to find a: a=(1−((Δl_1 sin θ_1 )/(Δl sin θ)))g

$${we}\:{even}\:{didn}'{t}\:{need}\:{m}\:{to}\:{find}\:{a}: \\ $$$${a}=\left(\mathrm{1}−\frac{\Delta{l}_{\mathrm{1}} \:\mathrm{sin}\:\theta_{\mathrm{1}} }{\Delta{l}\:\mathrm{sin}\:\theta}\right){g} \\ $$

Commented by Tawa11 last updated on 26/Mar/25

Yes, I observed it in your workings sir. God bless you always sir.

$$\mathrm{Yes},\:\mathrm{I}\:\mathrm{observed}\:\mathrm{it}\:\mathrm{in}\:\mathrm{your}\:\mathrm{workings}\:\mathrm{sir}. \\ $$$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{always}\:\mathrm{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com