Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 217937 by Tawa11 last updated on 23/Mar/25

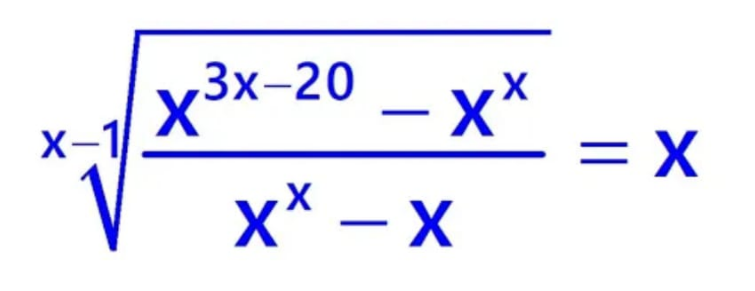
Commented by Tawa11 last updated on 23/Mar/25

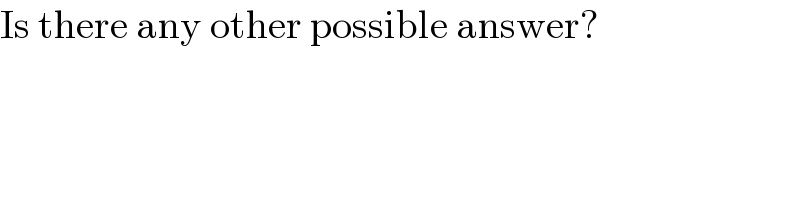
Is there any other possible answer?

$$\mathrm{Is}\:\mathrm{there}\:\mathrm{any}\:\mathrm{other}\:\mathrm{possible}\:\mathrm{answer}? \\ $$

Commented by Tawa11 last updated on 23/Mar/25

Solve for x. I got x = 19

$$\mathrm{Solve}\:\mathrm{for}\:\:\mathrm{x}. \\ $$$$\mathrm{I}\:\mathrm{got}\:\:\mathrm{x}\:\:=\:\:\mathrm{19} \\ $$

Commented by Ghisom last updated on 23/Mar/25

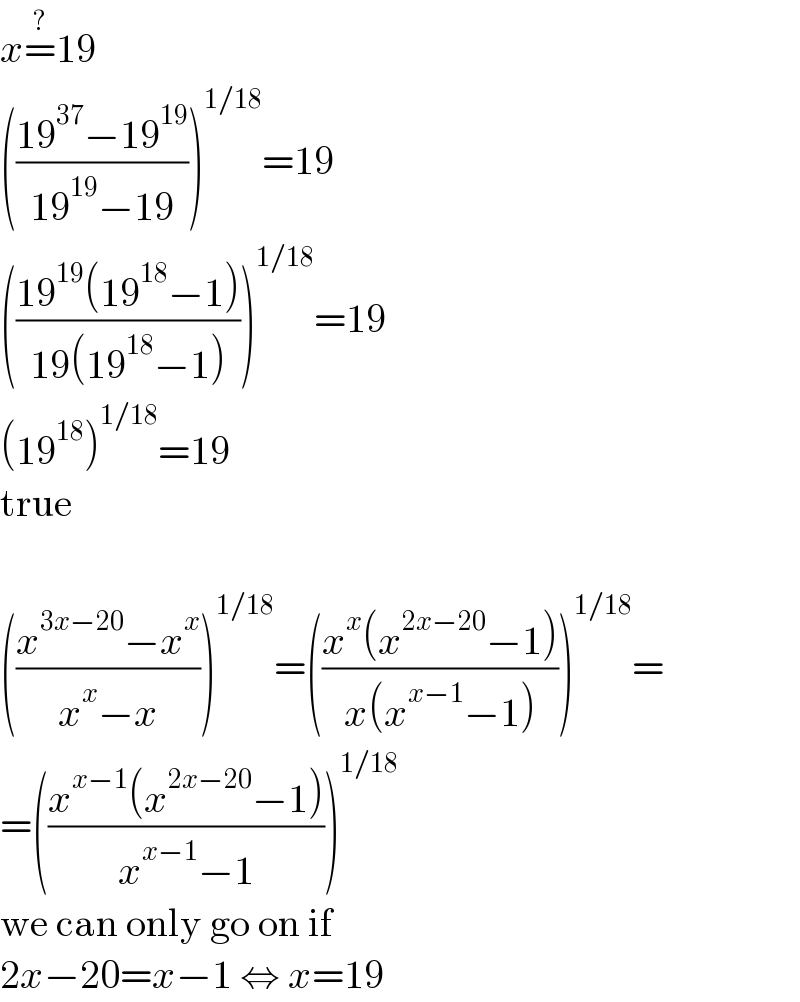
x=^? 19 (((19^(37) −19^(19) )/(19^(19) −19)))^(1/18) =19 (((19^(19) (19^(18) −1))/(19(19^(18) −1))))^(1/18) =19 (19^(18) )^(1/18) =19 true (((x^(3x−20) −x^x )/(x^x −x)))^(1/18) =(((x^x (x^(2x−20) −1))/(x(x^(x−1) −1))))^(1/18) = =(((x^(x−1) (x^(2x−20) −1))/(x^(x−1) −1)))^(1/18) we can only go on if 2x−20=x−1 ⇔ x=19

$${x}\overset{?} {=}\mathrm{19} \\ $$$$\left(\frac{\mathrm{19}^{\mathrm{37}} −\mathrm{19}^{\mathrm{19}} }{\mathrm{19}^{\mathrm{19}} −\mathrm{19}}\right)^{\mathrm{1}/\mathrm{18}} =\mathrm{19} \\ $$$$\left(\frac{\mathrm{19}^{\mathrm{19}} \left(\mathrm{19}^{\mathrm{18}} −\mathrm{1}\right)}{\mathrm{19}\left(\mathrm{19}^{\mathrm{18}} −\mathrm{1}\right)}\right)^{\mathrm{1}/\mathrm{18}} =\mathrm{19} \\ $$$$\left(\mathrm{19}^{\mathrm{18}} \right)^{\mathrm{1}/\mathrm{18}} =\mathrm{19} \\ $$$$\mathrm{true} \\ $$$$ \\ $$$$\left(\frac{{x}^{\mathrm{3}{x}−\mathrm{20}} −{x}^{{x}} }{{x}^{{x}} −{x}}\right)^{\mathrm{1}/\mathrm{18}} =\left(\frac{{x}^{{x}} \left({x}^{\mathrm{2}{x}−\mathrm{20}} −\mathrm{1}\right)}{{x}\left({x}^{{x}−\mathrm{1}} −\mathrm{1}\right)}\right)^{\mathrm{1}/\mathrm{18}} = \\ $$$$=\left(\frac{{x}^{{x}−\mathrm{1}} \left({x}^{\mathrm{2}{x}−\mathrm{20}} −\mathrm{1}\right)}{{x}^{{x}−\mathrm{1}} −\mathrm{1}}\right)^{\mathrm{1}/\mathrm{18}} \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{only}\:\mathrm{go}\:\mathrm{on}\:\mathrm{if} \\ $$$$\mathrm{2}{x}−\mathrm{20}={x}−\mathrm{1}\:\Leftrightarrow\:{x}=\mathrm{19} \\ $$

Commented by Tawa11 last updated on 23/Mar/25

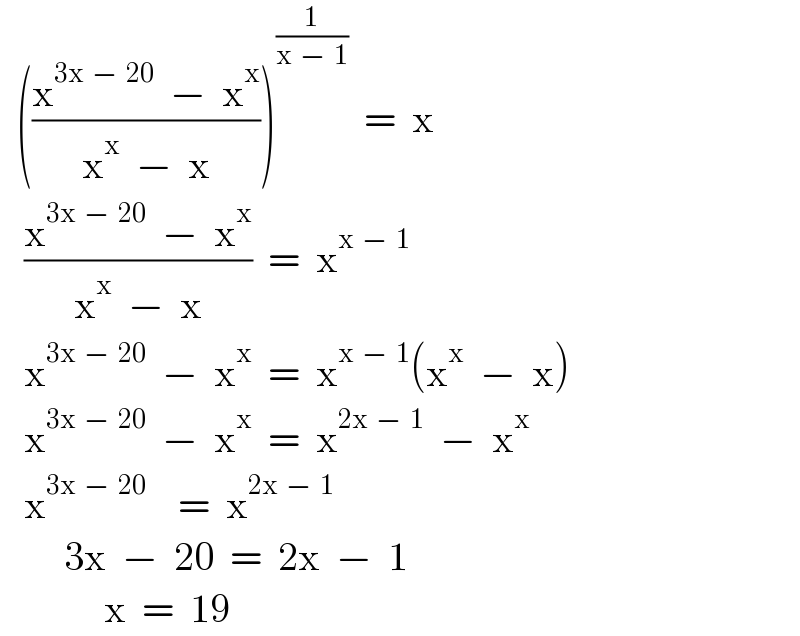
(((x^(3x − 20) − x^x )/(x^x − x)))^(1/(x − 1)) = x ((x^(3x − 20) − x^x )/(x^x − x)) = x^(x − 1) x^(3x − 20) − x^x = x^(x − 1) (x^x − x) x^(3x − 20) − x^x = x^(2x − 1) − x^x x^(3x − 20) = x^(2x − 1) 3x − 20 = 2x − 1 x = 19

$$\:\:\left(\frac{\mathrm{x}^{\mathrm{3x}\:\:−\:\:\mathrm{20}} \:\:−\:\:\mathrm{x}^{\mathrm{x}} }{\mathrm{x}^{\mathrm{x}} \:\:−\:\:\mathrm{x}}\right)^{\frac{\mathrm{1}}{\mathrm{x}\:\:−\:\:\mathrm{1}}} \:\:=\:\:\mathrm{x} \\ $$$$\:\:\:\frac{\mathrm{x}^{\mathrm{3x}\:\:−\:\:\mathrm{20}} \:\:−\:\:\mathrm{x}^{\mathrm{x}} }{\mathrm{x}^{\mathrm{x}} \:\:−\:\:\mathrm{x}}\:\:=\:\:\mathrm{x}^{\mathrm{x}\:\:−\:\:\mathrm{1}} \\ $$$$\:\:\:\mathrm{x}^{\mathrm{3x}\:\:−\:\:\mathrm{20}} \:\:−\:\:\mathrm{x}^{\mathrm{x}} \:\:=\:\:\mathrm{x}^{\mathrm{x}\:\:−\:\:\mathrm{1}} \left(\mathrm{x}^{\mathrm{x}} \:\:−\:\:\mathrm{x}\right) \\ $$$$\:\:\:\mathrm{x}^{\mathrm{3x}\:\:−\:\:\mathrm{20}} \:\:−\:\:\mathrm{x}^{\mathrm{x}} \:\:=\:\:\mathrm{x}^{\mathrm{2x}\:\:−\:\:\mathrm{1}} \:\:−\:\:\mathrm{x}^{\mathrm{x}} \\ $$$$\:\:\:\mathrm{x}^{\mathrm{3x}\:\:−\:\:\mathrm{20}} \:\:\:\:=\:\:\mathrm{x}^{\mathrm{2x}\:\:−\:\:\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{3x}\:\:−\:\:\mathrm{20}\:\:=\:\:\mathrm{2x}\:\:−\:\:\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{x}\:\:=\:\:\mathrm{19} \\ $$

Commented by Tawa11 last updated on 23/Mar/25

19 is possible sir.

$$\mathrm{19}\:\mathrm{is}\:\mathrm{possible}\:\mathrm{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com