
Question Number 217691 by PaulDirac last updated on 18/Mar/25
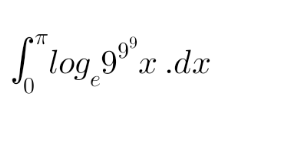
Answered by mr W last updated on 19/Mar/25
![let a=9^9^9 I=∫_0 ^π ln (ax)dx =(1/a)∫_0 ^π ln (ax)d(ax) =(1/a)∫_0 ^(aπ) ln t dt =(1/a){[t ln t]_0 ^(aπ) −∫_0 ^(aπ) dt} =(1/a)[t(ln t−1)]_0 ^(aπ) =(1/a)×aπ(ln aπ−1)−(1/a)lim_(t→0) t(ln t−1) =π(ln aπ−1)−(1/a)lim_(t→0) (ln t^t −t) ^(∗)) =π(ln aπ−1) =π[ln (9^9^9 π)−1] ✓ ^(∗)) Note: lim_(x→0) x^x =1 ⇒lim_(x→0) (ln x^x )=0](Q217707.png)
$${let}\:{a}=\mathrm{9}^{\mathrm{9}^{\mathrm{9}} } \\ $$$${I}=\int_{\mathrm{0}} ^{\pi} \mathrm{ln}\:\left({ax}\right){dx} \\ $$$$\:\:=\frac{\mathrm{1}}{{a}}\int_{\mathrm{0}} ^{\pi} \mathrm{ln}\:\left({ax}\right){d}\left({ax}\right) \\ $$$$\:\:=\frac{\mathrm{1}}{{a}}\int_{\mathrm{0}} ^{{a}\pi} \mathrm{ln}\:{t}\:{dt} \\ $$$$\:\:=\frac{\mathrm{1}}{{a}}\left\{\left[{t}\:\mathrm{ln}\:{t}\right]_{\mathrm{0}} ^{{a}\pi} −\int_{\mathrm{0}} ^{{a}\pi} {dt}\right\} \\ $$$$\:\:=\frac{\mathrm{1}}{{a}}\left[{t}\left(\mathrm{ln}\:{t}−\mathrm{1}\right)\right]_{\mathrm{0}} ^{{a}\pi} \\ $$$$\:\:=\frac{\mathrm{1}}{{a}}×{a}\pi\left(\mathrm{ln}\:{a}\pi−\mathrm{1}\right)−\frac{\mathrm{1}}{{a}}\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{t}\left(\mathrm{ln}\:{t}−\mathrm{1}\right) \\ $$$$\:\:=\pi\left(\mathrm{ln}\:{a}\pi−\mathrm{1}\right)−\frac{\mathrm{1}}{{a}}\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\mathrm{ln}\:{t}^{{t}} −{t}\right)\:\:\:\:\:\:^{\left.\ast\right)} \\ $$$$\:\:=\pi\left(\mathrm{ln}\:{a}\pi−\mathrm{1}\right) \\ $$$$\:\:=\pi\left[\mathrm{ln}\:\left(\mathrm{9}^{\mathrm{9}^{\mathrm{9}} } \pi\right)−\mathrm{1}\right]\:\checkmark \\ $$$$ \\ $$$$\:^{\left.\ast\right)} \:{Note}: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{x}^{{x}} =\mathrm{1}\:\Rightarrow\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{ln}\:{x}^{{x}} \right)=\mathrm{0} \\ $$
Commented by SdC355 last updated on 19/Mar/25

$$\mathrm{sorry},\:\mathrm{i}\:\mathrm{was}\:\mathrm{careless}. \\ $$
Commented by mr W last updated on 19/Mar/25
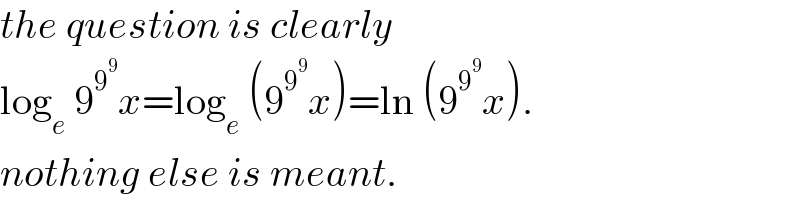
$${the}\:{question}\:{is}\:{clearly} \\ $$$$\mathrm{log}_{{e}} \:\mathrm{9}^{\mathrm{9}^{\mathrm{9}} } {x}=\mathrm{log}_{{e}} \:\left(\mathrm{9}^{\mathrm{9}^{\mathrm{9}} } {x}\right)=\mathrm{ln}\:\left(\mathrm{9}^{\mathrm{9}^{\mathrm{9}} } {x}\right). \\ $$$${nothing}\:{else}\:{is}\:{meant}. \\ $$
Commented by mr W last updated on 19/Mar/25
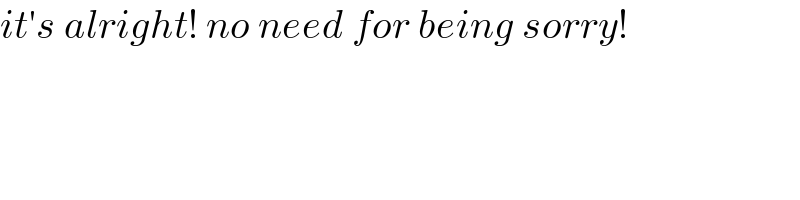
$${it}'{s}\:{alright}!\:{no}\:{need}\:{for}\:{being}\:{sorry}! \\ $$
Commented by SdC355 last updated on 19/Mar/25
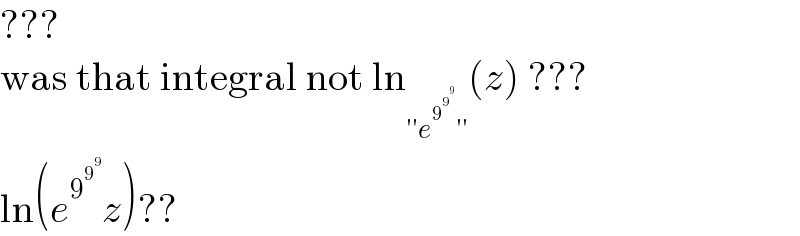
$$??? \\ $$$$\mathrm{was}\:\mathrm{that}\:\mathrm{integral}\:\mathrm{not}\:\mathrm{ln}_{''{e}^{\mathrm{9}^{\mathrm{9}^{\mathrm{9}} } } ''} \left({z}\right)\:??? \\ $$$$\mathrm{ln}\left({e}^{\mathrm{9}^{\mathrm{9}^{\mathrm{9}} } } {z}\right)?? \\ $$
Answered by Wuji last updated on 19/Mar/25
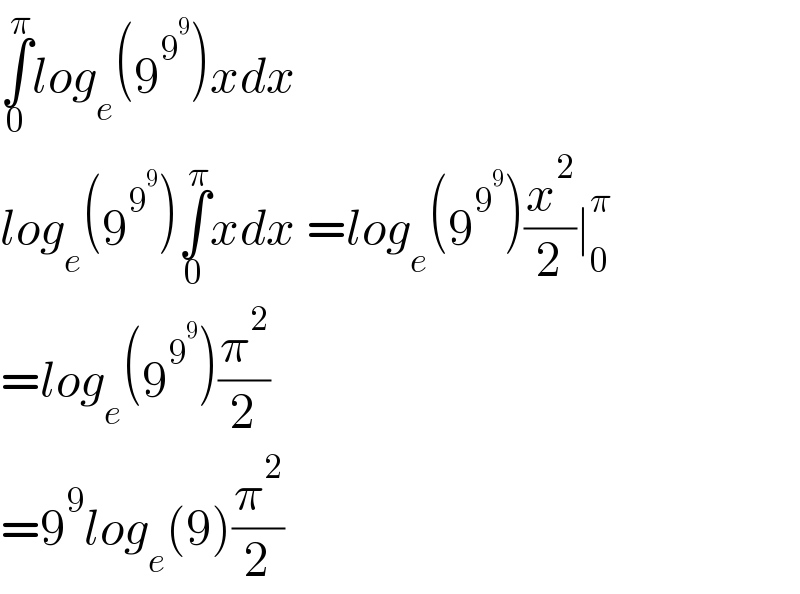
$$\underset{\mathrm{0}} {\overset{\pi} {\int}}{log}_{{e}} \left(\mathrm{9}^{\mathrm{9}^{\mathrm{9}} } \right){xdx} \\ $$$${log}_{{e}} \left(\mathrm{9}^{\mathrm{9}^{\mathrm{9}} } \right)\underset{\mathrm{0}} {\overset{\pi} {\int}}{xdx}\:={log}_{{e}} \left(\mathrm{9}^{\mathrm{9}^{\mathrm{9}} } \right)\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\mid_{\mathrm{0}} ^{\pi} \: \\ $$$$={log}_{{e}} \left(\mathrm{9}^{\mathrm{9}^{\mathrm{9}} } \right)\frac{\pi^{\mathrm{2}} }{\mathrm{2}} \\ $$$$=\mathrm{9}^{\mathrm{9}} {log}_{{e}} \left(\mathrm{9}\right)\frac{\pi^{\mathrm{2}} }{\mathrm{2}} \\ $$
Commented by mr W last updated on 20/Mar/25
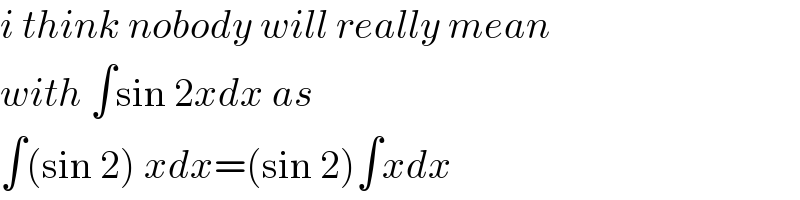
$${i}\:{think}\:{nobody}\:{will}\:{really}\:{mean} \\ $$$${with}\:\int\mathrm{sin}\:\mathrm{2}{xdx}\:{as}\: \\ $$$$\int\left(\mathrm{sin}\:\mathrm{2}\right)\:{xdx}=\left(\mathrm{sin}\:\mathrm{2}\right)\int{xdx} \\ $$
Commented by Wuji last updated on 22/Mar/25
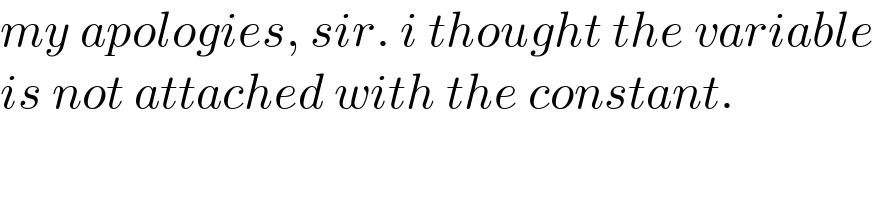
$${my}\:{apologies},\:{sir}.\:{i}\:{thought}\:{the}\:{variable} \\ $$$${is}\:{not}\:{attached}\:{with}\:{the}\:{constant}. \\ $$
Answered by Wuji last updated on 22/Mar/25
![Thanks to Mr. W for pointing out my errors ∫_0 ^π log_e (9^9^9 x)dx =∫_0 ^π ln(9^9^9 x)dx I(a)=∫_0 ^π ln(ax)dx {a=9^9^9 } (d/da)I(a)=∫_0 ^π (d/da)ln(ax)dx=∫_0 ^π (1/(ax))xdx=∫_0 ^π (1/a)dx=(π/a) I(a)=∫_0 ^π (π/a)da =πln(a)+C I(1)=∫_0 ^π ln(x)dx =xln(x)−x+C I(1)=[πln(π)−π]−lim_(x→0^+ ) (xln(x)−x)=πln(π)−π I(a)=πln(a)+πln(π)−π=π(ln(aπ)−1) a=9^9^9 I=π[ln(9^9^9 π)−1] =π(9^9 ln(9π)−1)](Q217864.png)
$${Thanks}\:{to}\:{Mr}.\:{W}\:{for}\:{pointing}\:{out}\:{my}\:{errors} \\ $$$$\int_{\mathrm{0}} ^{\pi} {log}_{{e}} \left(\mathrm{9}^{\mathrm{9}^{\mathrm{9}} } {x}\right){dx}\:\:=\int_{\mathrm{0}} ^{\pi} {ln}\left(\mathrm{9}^{\mathrm{9}^{\mathrm{9}} } {x}\right){dx} \\ $$$${I}\left({a}\right)=\int_{\mathrm{0}} ^{\pi} {ln}\left({ax}\right){dx}\:\:\:\:\left\{{a}=\mathrm{9}^{\mathrm{9}^{\mathrm{9}} } \right\} \\ $$$$\frac{{d}}{{da}}{I}\left({a}\right)=\int_{\mathrm{0}} ^{\pi} \frac{{d}}{{da}}{ln}\left({ax}\right){dx}=\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{1}}{{ax}}{xdx}=\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{1}}{{a}}{dx}=\frac{\pi}{{a}} \\ $$$${I}\left({a}\right)=\int_{\mathrm{0}} ^{\pi} \frac{\pi}{{a}}{da}\:=\pi{ln}\left({a}\right)+{C} \\ $$$${I}\left(\mathrm{1}\right)=\int_{\mathrm{0}} ^{\pi} {ln}\left({x}\right){dx}\:\:={xln}\left({x}\right)−{x}+{C} \\ $$$${I}\left(\mathrm{1}\right)=\left[\pi{ln}\left(\pi\right)−\pi\right]−\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\left({xln}\left({x}\right)−{x}\right)=\pi{ln}\left(\pi\right)−\pi \\ $$$${I}\left({a}\right)=\pi{ln}\left({a}\right)+\pi{ln}\left(\pi\right)−\pi=\pi\left({ln}\left({a}\pi\right)−\mathrm{1}\right) \\ $$$${a}=\mathrm{9}^{\mathrm{9}^{\mathrm{9}} } \\ $$$${I}=\pi\left[{ln}\left(\mathrm{9}^{\mathrm{9}^{\mathrm{9}} } \pi\right)−\mathrm{1}\right]\:=\pi\left(\mathrm{9}^{\mathrm{9}} {ln}\left(\mathrm{9}\pi\right)−\mathrm{1}\right) \\ $$
