Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 217640 by Tawa11 last updated on 17/Mar/25

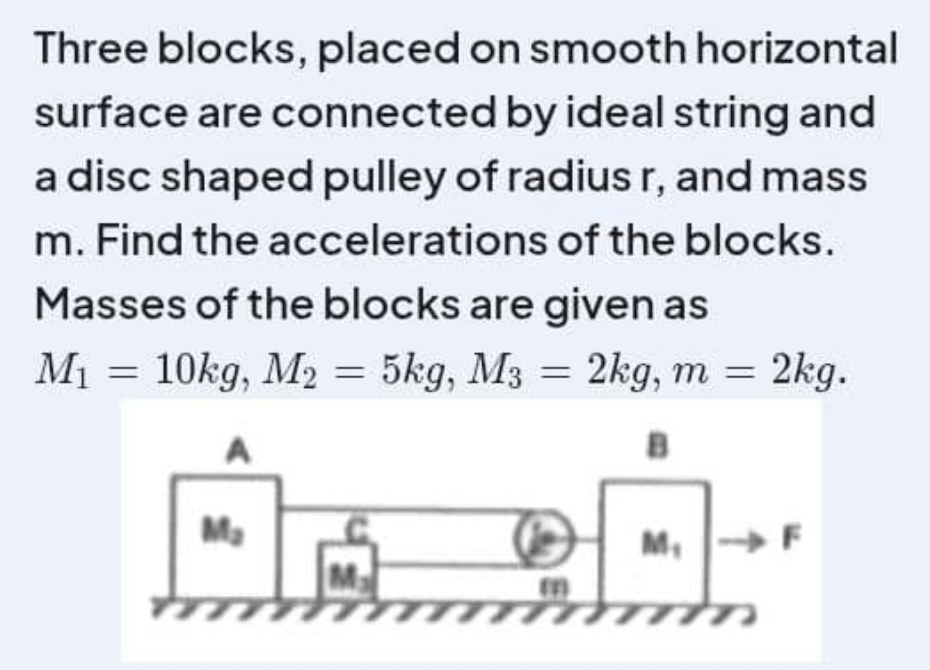
Commented by mr W last updated on 17/Mar/25

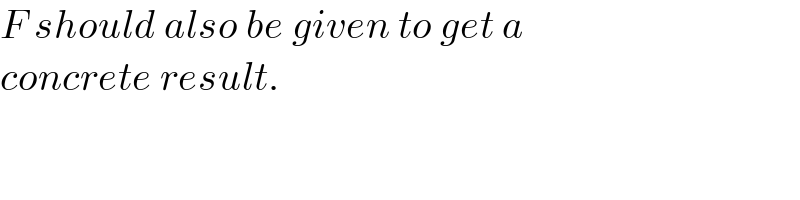
F should also be given to get a concrete result.

$${F}\:{should}\:{also}\:{be}\:{given}\:{to}\:{get}\:{a} \\ $$$${concrete}\:{result}. \\ $$

Answered by mahdipoor last updated on 17/Mar/25

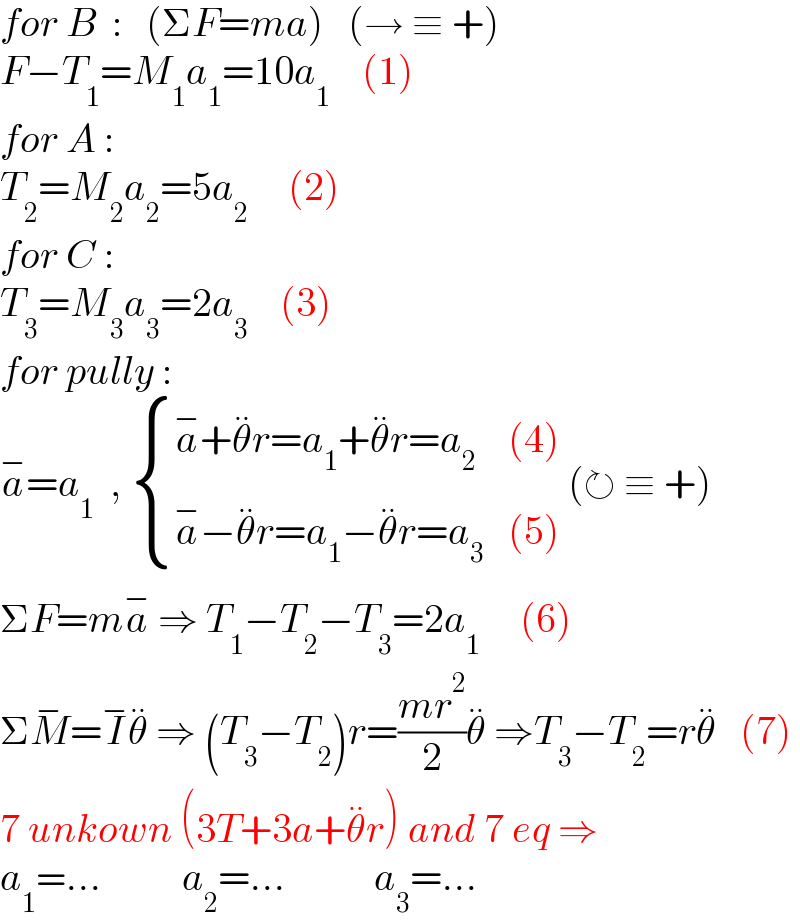
for B : (ΣF=ma) (→ ≡ +) F−T_1 =M_1 a_1 =10a_1 (1) for A : T_2 =M_2 a_2 =5a_2 (2) for C : T_3 =M_3 a_3 =2a_3 (3) for pully : a^− =a_1 , { ((a^− +θ^(..) r=a_1 +θ^(..) r=a_2 (4))),((a^− −θ^(..) r=a_1 −θ^(..) r=a_3 (5))) :} (↻ ≡ +) ΣF=ma^− ⇒ T_1 −T_2 −T_3 =2a_1 (6) ΣM^− =I^− θ^(..) ⇒ (T_3 −T_2 )r=((mr^2 )/2)θ^(..) ⇒T_3 −T_2 =rθ^(..) (7) 7 unkown (3T+3a+θ^(..) r) and 7 eq ⇒ a_1 =... a_2 =... a_3 =...

$${for}\:{B}\:\::\:\:\:\left(\Sigma{F}={ma}\right)\:\:\:\left(\rightarrow\:\equiv\:+\right) \\ $$$${F}−{T}_{\mathrm{1}} ={M}_{\mathrm{1}} {a}_{\mathrm{1}} =\mathrm{10}{a}_{\mathrm{1}} \:\:\:\:\left(\mathrm{1}\right) \\ $$$${for}\:{A}\:: \\ $$$${T}_{\mathrm{2}} ={M}_{\mathrm{2}} {a}_{\mathrm{2}} =\mathrm{5}{a}_{\mathrm{2}} \:\:\:\:\:\left(\mathrm{2}\right) \\ $$$${for}\:{C}\:: \\ $$$${T}_{\mathrm{3}} ={M}_{\mathrm{3}} {a}_{\mathrm{3}} =\mathrm{2}{a}_{\mathrm{3}} \:\:\:\:\left(\mathrm{3}\right) \\ $$$${for}\:{pully}\:: \\ $$$$\overset{−} {{a}}={a}_{\mathrm{1}} \:\:,\:\begin{cases}{\overset{−} {{a}}+\overset{..} {\theta}{r}={a}_{\mathrm{1}} +\overset{..} {\theta}{r}={a}_{\mathrm{2}} \:\:\:\:\left(\mathrm{4}\right)}\\{\overset{−} {{a}}−\overset{..} {\theta}{r}={a}_{\mathrm{1}} −\overset{..} {\theta}{r}={a}_{\mathrm{3}} \:\:\:\left(\mathrm{5}\right)}\end{cases}\:\left(\circlearrowright\:\equiv\:+\right) \\ $$$$\Sigma{F}={m}\overset{−} {{a}}\:\Rightarrow\:{T}_{\mathrm{1}} −{T}_{\mathrm{2}} −{T}_{\mathrm{3}} =\mathrm{2}{a}_{\mathrm{1}} \:\:\:\:\:\left(\mathrm{6}\right) \\ $$$$\Sigma\overset{−} {{M}}=\overset{−} {{I}}\overset{..} {\theta}\:\Rightarrow\:\left({T}_{\mathrm{3}} −{T}_{\mathrm{2}} \right){r}=\frac{{mr}^{\mathrm{2}} }{\mathrm{2}}\overset{..} {\theta}\:\Rightarrow{T}_{\mathrm{3}} −{T}_{\mathrm{2}} ={r}\overset{..} {\theta}\:\:\:\left(\mathrm{7}\right) \\ $$$$\mathrm{7}\:{unkown}\:\left(\mathrm{3}{T}+\mathrm{3}{a}+\overset{..} {\theta}{r}\right)\:{and}\:\mathrm{7}\:{eq}\:\Rightarrow \\ $$$${a}_{\mathrm{1}} =...\:\:\:\:\:\:\:\:\:\:{a}_{\mathrm{2}} =...\:\:\:\:\:\:\:\:\:\:\:{a}_{\mathrm{3}} =... \\ $$

Commented by Tawa11 last updated on 17/Mar/25

Thanks sir. I appreciate.

$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$$$\mathrm{I}\:\mathrm{appreciate}. \\ $$

Answered by mr W last updated on 17/Mar/25

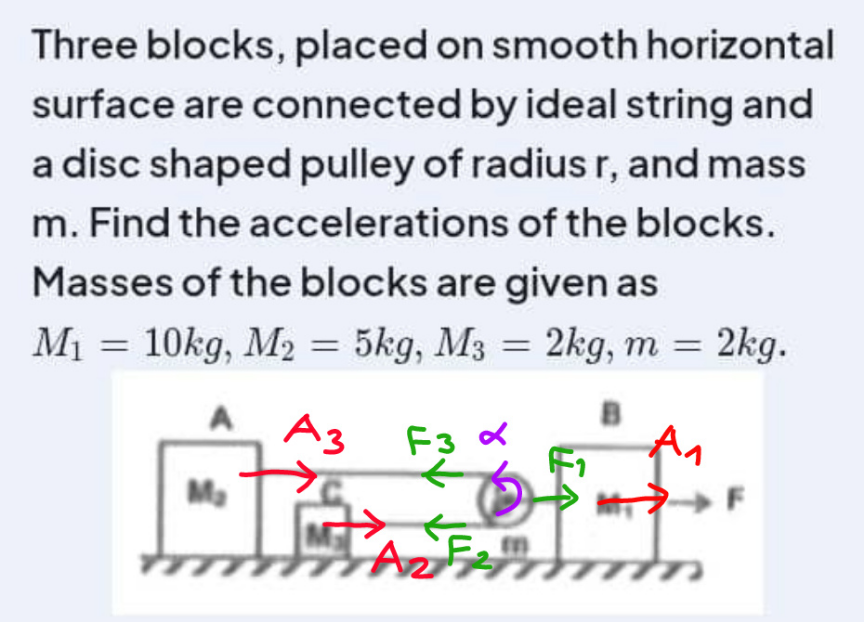
Commented by mr W last updated on 17/Mar/25

α=angular acc. of pulley (↶) A_1 =acc. of M_1 and m A_2 =acc. of M_2 =A_1 +αr A_3 =acc. of M_3 =A_1 −αr F_2 =M_2 A_2 =M_2 (A_1 +αr) F_3 =M_3 A_3 =M_3 (A_1 −αr) F−F_2 −F_3 =(M_1 +m)A_1 F=(M_1 +m)A_1 +M_2 (A_1 +αr)+M_3 (A_1 −αr) ⇒(M_1 +m+M_2 +M_3 )A_1 +(M_2 −M_3 )αr=F ...(i) F_3 r−F_2 r=Iα=((mr^2 α)/2) M_3 (A_1 −αr)−M_2 (A_1 +αr)=((mrα)/2) ⇒(M_2 −M_3 )A_1 +(M_2 +M_3 +(m/2))αr=0 ...(ii) from (ii): αr=−(((M_2 −M_3 )A_1 )/((M_2 +M_3 +(m/2)))) this into (i): [M_1 +m+M_2 +M_3 −(((M_2 −M_3 )^2 )/(M_2 +M_3 +(m/2)))]A_1 =F ⇒A_1 =(F/(M_1 +m+M_2 +M_3 −(((M_2 −M_3 )^2 )/(M_2 +M_3 +(m/2))))) ⇒A_2 =(1−((M_2 −M_3 )/(M_2 +M_3 +(m/2))))(F/(M_1 +m+M_2 +M_3 −(((M_2 −M_3 )^2 )/(M_2 +M_3 +(m/2))))) ⇒A_3 =(1+((M_2 −M_3 )/(M_2 +M_3 +(m/2))))(F/(M_1 +m+M_2 +M_3 −(((M_2 −M_3 )^2 )/(M_2 +M_3 +(m/2)))))

$$\alpha={angular}\:{acc}.\:{of}\:{pulley}\:\left(\curvearrowleft\right) \\ $$$${A}_{\mathrm{1}} ={acc}.\:{of}\:{M}_{\mathrm{1}} \:{and}\:{m} \\ $$$${A}_{\mathrm{2}} ={acc}.\:{of}\:{M}_{\mathrm{2}} ={A}_{\mathrm{1}} +\alpha{r} \\ $$$${A}_{\mathrm{3}} ={acc}.\:{of}\:{M}_{\mathrm{3}} ={A}_{\mathrm{1}} −\alpha{r} \\ $$$$ \\ $$$${F}_{\mathrm{2}} ={M}_{\mathrm{2}} {A}_{\mathrm{2}} ={M}_{\mathrm{2}} \left({A}_{\mathrm{1}} +\alpha{r}\right) \\ $$$${F}_{\mathrm{3}} ={M}_{\mathrm{3}} {A}_{\mathrm{3}} ={M}_{\mathrm{3}} \left({A}_{\mathrm{1}} −\alpha{r}\right) \\ $$$${F}−{F}_{\mathrm{2}} −{F}_{\mathrm{3}} =\left({M}_{\mathrm{1}} +{m}\right){A}_{\mathrm{1}} \\ $$$${F}=\left({M}_{\mathrm{1}} +{m}\right){A}_{\mathrm{1}} +{M}_{\mathrm{2}} \left({A}_{\mathrm{1}} +\alpha{r}\right)+{M}_{\mathrm{3}} \left({A}_{\mathrm{1}} −\alpha{r}\right) \\ $$$$\Rightarrow\left({M}_{\mathrm{1}} +{m}+{M}_{\mathrm{2}} +{M}_{\mathrm{3}} \right){A}_{\mathrm{1}} +\left({M}_{\mathrm{2}} −{M}_{\mathrm{3}} \right)\alpha{r}={F}\:\:\:...\left({i}\right) \\ $$$$ \\ $$$${F}_{\mathrm{3}} {r}−{F}_{\mathrm{2}} {r}={I}\alpha=\frac{{mr}^{\mathrm{2}} \alpha}{\mathrm{2}} \\ $$$${M}_{\mathrm{3}} \left({A}_{\mathrm{1}} −\alpha{r}\right)−{M}_{\mathrm{2}} \left({A}_{\mathrm{1}} +\alpha{r}\right)=\frac{{mr}\alpha}{\mathrm{2}} \\ $$$$\Rightarrow\left({M}_{\mathrm{2}} −{M}_{\mathrm{3}} \right){A}_{\mathrm{1}} +\left({M}_{\mathrm{2}} +{M}_{\mathrm{3}} +\frac{{m}}{\mathrm{2}}\right)\alpha{r}=\mathrm{0}\:\:\:...\left({ii}\right) \\ $$$${from}\:\left({ii}\right): \\ $$$$\alpha{r}=−\frac{\left({M}_{\mathrm{2}} −{M}_{\mathrm{3}} \right){A}_{\mathrm{1}} }{\left({M}_{\mathrm{2}} +{M}_{\mathrm{3}} +\frac{{m}}{\mathrm{2}}\right)} \\ $$$${this}\:{into}\:\left({i}\right): \\ $$$$\left[{M}_{\mathrm{1}} +{m}+{M}_{\mathrm{2}} +{M}_{\mathrm{3}} −\frac{\left({M}_{\mathrm{2}} −{M}_{\mathrm{3}} \right)^{\mathrm{2}} }{{M}_{\mathrm{2}} +{M}_{\mathrm{3}} +\frac{{m}}{\mathrm{2}}}\right]{A}_{\mathrm{1}} ={F} \\ $$$$\Rightarrow{A}_{\mathrm{1}} =\frac{{F}}{{M}_{\mathrm{1}} +{m}+{M}_{\mathrm{2}} +{M}_{\mathrm{3}} −\frac{\left({M}_{\mathrm{2}} −{M}_{\mathrm{3}} \right)^{\mathrm{2}} }{{M}_{\mathrm{2}} +{M}_{\mathrm{3}} +\frac{{m}}{\mathrm{2}}}} \\ $$$$\Rightarrow{A}_{\mathrm{2}} =\left(\mathrm{1}−\frac{{M}_{\mathrm{2}} −{M}_{\mathrm{3}} }{{M}_{\mathrm{2}} +{M}_{\mathrm{3}} +\frac{{m}}{\mathrm{2}}}\right)\frac{{F}}{{M}_{\mathrm{1}} +{m}+{M}_{\mathrm{2}} +{M}_{\mathrm{3}} −\frac{\left({M}_{\mathrm{2}} −{M}_{\mathrm{3}} \right)^{\mathrm{2}} }{{M}_{\mathrm{2}} +{M}_{\mathrm{3}} +\frac{{m}}{\mathrm{2}}}} \\ $$$$\Rightarrow{A}_{\mathrm{3}} =\left(\mathrm{1}+\frac{{M}_{\mathrm{2}} −{M}_{\mathrm{3}} }{{M}_{\mathrm{2}} +{M}_{\mathrm{3}} +\frac{{m}}{\mathrm{2}}}\right)\frac{{F}}{{M}_{\mathrm{1}} +{m}+{M}_{\mathrm{2}} +{M}_{\mathrm{3}} −\frac{\left({M}_{\mathrm{2}} −{M}_{\mathrm{3}} \right)^{\mathrm{2}} }{{M}_{\mathrm{2}} +{M}_{\mathrm{3}} +\frac{{m}}{\mathrm{2}}}} \\ $$

Commented by Tawa11 last updated on 17/Mar/25

Great sir. Weldone. I appreciate sir.

$$\mathrm{Great}\:\mathrm{sir}. \\ $$$$\mathrm{Weldone}. \\ $$$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{sir}. \\ $$

Commented by Tawa11 last updated on 17/Mar/25

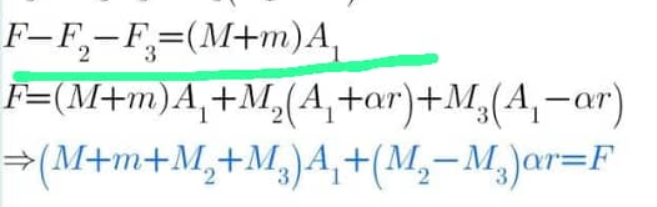
Commented by Tawa11 last updated on 17/Mar/25

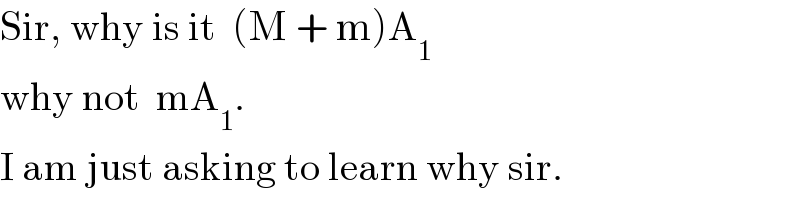
Sir, why is it (M + m)A_1 why not mA_1 . I am just asking to learn why sir.

$$\mathrm{Sir},\:\mathrm{why}\:\mathrm{is}\:\mathrm{it}\:\:\left(\mathrm{M}\:+\:\mathrm{m}\right)\mathrm{A}_{\mathrm{1}} \\ $$$$\mathrm{why}\:\mathrm{not}\:\:\mathrm{mA}_{\mathrm{1}} . \\ $$$$\mathrm{I}\:\mathrm{am}\:\mathrm{just}\:\mathrm{asking}\:\mathrm{to}\:\mathrm{learn}\:\mathrm{why}\:\mathrm{sir}. \\ $$

Commented by mr W last updated on 17/Mar/25

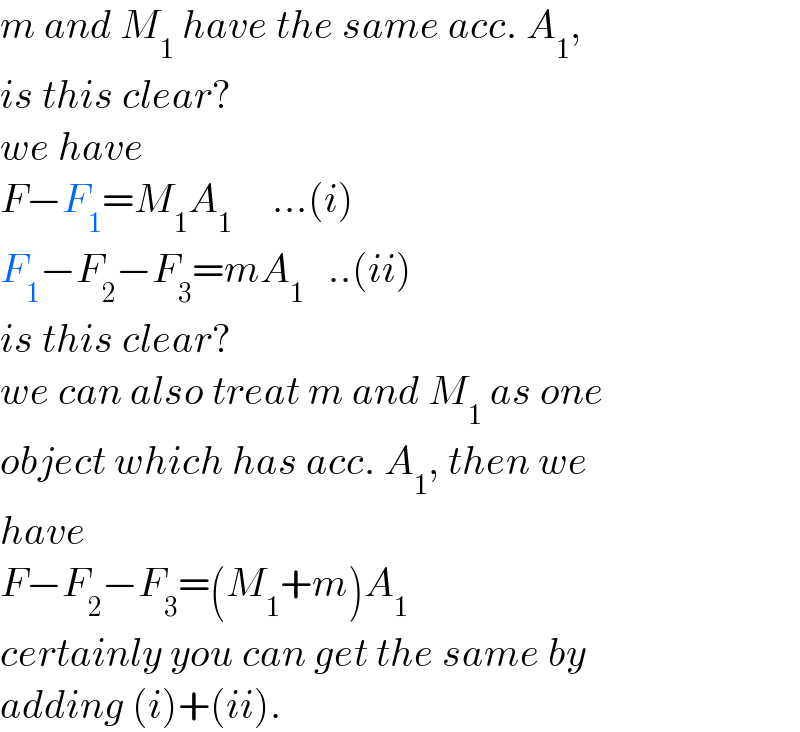
m and M_1 have the same acc. A_1 , is this clear? we have F−F_1 =M_1 A_1 ...(i) F_1 −F_2 −F_3 =mA_1 ..(ii) is this clear? we can also treat m and M_1 as one object which has acc. A_1 , then we have F−F_2 −F_3 =(M_1 +m)A_1 certainly you can get the same by adding (i)+(ii).

$${m}\:{and}\:{M}_{\mathrm{1}} \:{have}\:{the}\:{same}\:{acc}.\:{A}_{\mathrm{1}} , \\ $$$${is}\:{this}\:{clear}? \\ $$$${we}\:{have} \\ $$$${F}−{F}_{\mathrm{1}} ={M}_{\mathrm{1}} {A}_{\mathrm{1}} \:\:\:\:\:...\left({i}\right) \\ $$$${F}_{\mathrm{1}} −{F}_{\mathrm{2}} −{F}_{\mathrm{3}} ={mA}_{\mathrm{1}} \:\:\:..\left({ii}\right) \\ $$$${is}\:{this}\:{clear}? \\ $$$${we}\:{can}\:{also}\:{treat}\:{m}\:{and}\:{M}_{\mathrm{1}} \:{as}\:{one} \\ $$$${object}\:{which}\:{has}\:{acc}.\:{A}_{\mathrm{1}} ,\:{then}\:{we}\: \\ $$$${have} \\ $$$${F}−{F}_{\mathrm{2}} −{F}_{\mathrm{3}} =\left({M}_{\mathrm{1}} +{m}\right){A}_{\mathrm{1}} \\ $$$${certainly}\:{you}\:{can}\:{get}\:{the}\:{same}\:{by} \\ $$$${adding}\:\left({i}\right)+\left({ii}\right). \\ $$

Commented by Tawa11 last updated on 17/Mar/25

I understand now. Thank you sir.

$$\mathrm{I}\:\mathrm{understand}\:\mathrm{now}. \\ $$$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com