Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 217631 by mnjuly1970 last updated on 17/Mar/25

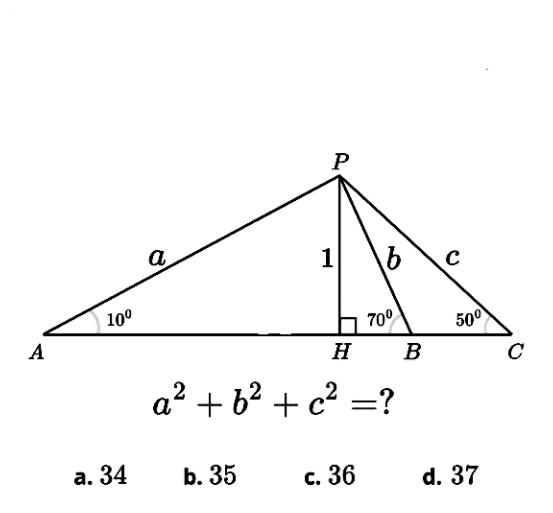
Commented by mnjuly1970 last updated on 17/Mar/25

yes . that′s right.thanks alot sir

$$\:{yes}\:.\:{that}'{s}\:{right}.{thanks}\:{alot}\:{sir} \\ $$

Answered by maths2 last updated on 17/Mar/25

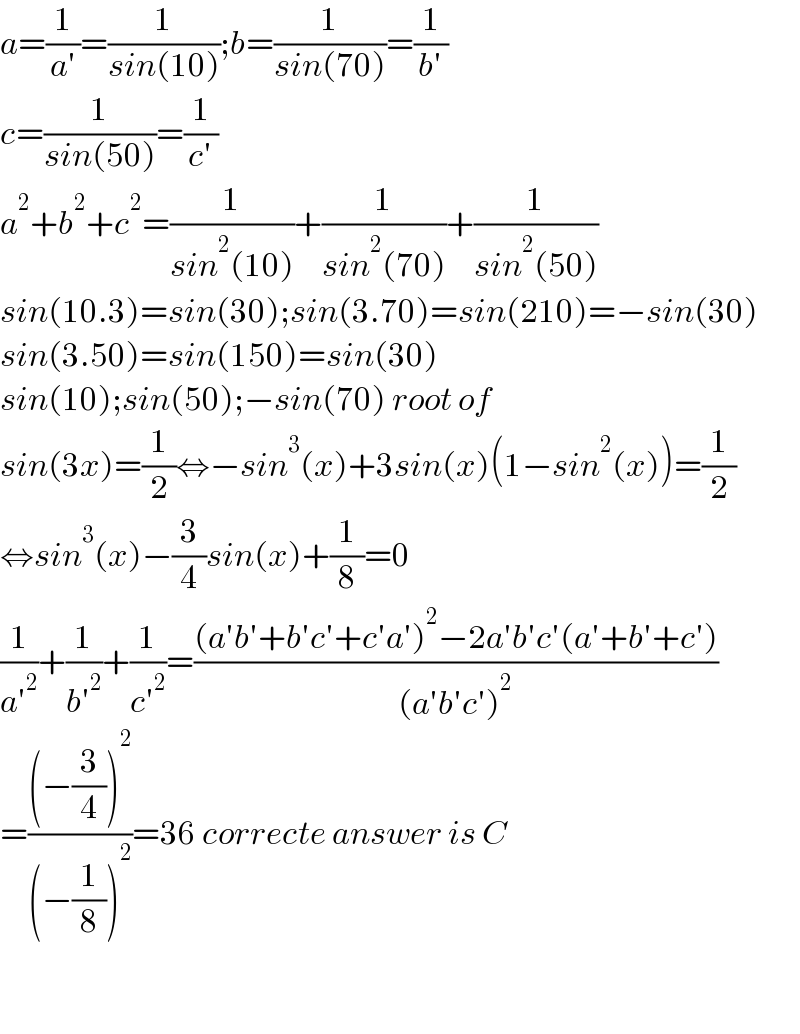
a=(1/(a′))=(1/(sin(10)));b=(1/(sin(70)))=(1/(b′)) c=(1/(sin(50)))=(1/(c′)) a^2 +b^2 +c^2 =(1/(sin^2 (10)))+(1/(sin^2 (70)))+(1/(sin^2 (50))) sin(10.3)=sin(30);sin(3.70)=sin(210)=−sin(30) sin(3.50)=sin(150)=sin(30) sin(10);sin(50);−sin(70) root of sin(3x)=(1/2)⇔−sin^3 (x)+3sin(x)(1−sin^2 (x))=(1/2) ⇔sin^3 (x)−(3/4)sin(x)+(1/8)=0 (1/(a′^2 ))+(1/(b′^2 ))+(1/(c′^2 ))=(((a′b′+b′c′+c′a′)^2 −2a′b′c′(a′+b′+c′))/((a′b′c′)^2 )) =(((−(3/4))^2 )/((−(1/8))^2 ))=36 correcte answer is C

$${a}=\frac{\mathrm{1}}{{a}'}=\frac{\mathrm{1}}{{sin}\left(\mathrm{10}\right)};{b}=\frac{\mathrm{1}}{{sin}\left(\mathrm{70}\right)}=\frac{\mathrm{1}}{{b}'} \\ $$$${c}=\frac{\mathrm{1}}{{sin}\left(\mathrm{50}\right)}=\frac{\mathrm{1}}{{c}'} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} =\frac{\mathrm{1}}{{sin}^{\mathrm{2}} \left(\mathrm{10}\right)}+\frac{\mathrm{1}}{{sin}^{\mathrm{2}} \left(\mathrm{70}\right)}+\frac{\mathrm{1}}{{sin}^{\mathrm{2}} \left(\mathrm{50}\right)} \\ $$$${sin}\left(\mathrm{10}.\mathrm{3}\right)={sin}\left(\mathrm{30}\right);{sin}\left(\mathrm{3}.\mathrm{70}\right)={sin}\left(\mathrm{210}\right)=−{sin}\left(\mathrm{30}\right) \\ $$$${sin}\left(\mathrm{3}.\mathrm{50}\right)={sin}\left(\mathrm{150}\right)={sin}\left(\mathrm{30}\right) \\ $$$${sin}\left(\mathrm{10}\right);{sin}\left(\mathrm{50}\right);−{sin}\left(\mathrm{70}\right)\:{root}\:{of} \\ $$$${sin}\left(\mathrm{3}{x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\Leftrightarrow−{sin}^{\mathrm{3}} \left({x}\right)+\mathrm{3}{sin}\left({x}\right)\left(\mathrm{1}−{sin}^{\mathrm{2}} \left({x}\right)\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Leftrightarrow{sin}^{\mathrm{3}} \left({x}\right)−\frac{\mathrm{3}}{\mathrm{4}}{sin}\left({x}\right)+\frac{\mathrm{1}}{\mathrm{8}}=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{{a}'^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}'^{\mathrm{2}} }+\frac{\mathrm{1}}{{c}'^{\mathrm{2}} }=\frac{\left({a}'{b}'+{b}'{c}'+{c}'{a}'\right)^{\mathrm{2}} −\mathrm{2}{a}'{b}'{c}'\left({a}'+{b}'+{c}'\right)}{\left({a}'{b}'{c}'\right)^{\mathrm{2}} } \\ $$$$=\frac{\left(−\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{2}} }{\left(−\frac{\mathrm{1}}{\mathrm{8}}\right)^{\mathrm{2}} }=\mathrm{36}\:{correcte}\:{answer}\:{is}\:{C} \\ $$$$ \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com