Question and Answers Forum

All Questions      Topic List

Mechanics Questions

Previous in All Question      Next in All Question      

Previous in Mechanics      Next in Mechanics      

Question Number 217565 by mr W last updated on 16/Mar/25

Commented by mr W last updated on 16/Mar/25

the strings are massless and there is no friction between strings and pulleys. find the accelerations of all objects.

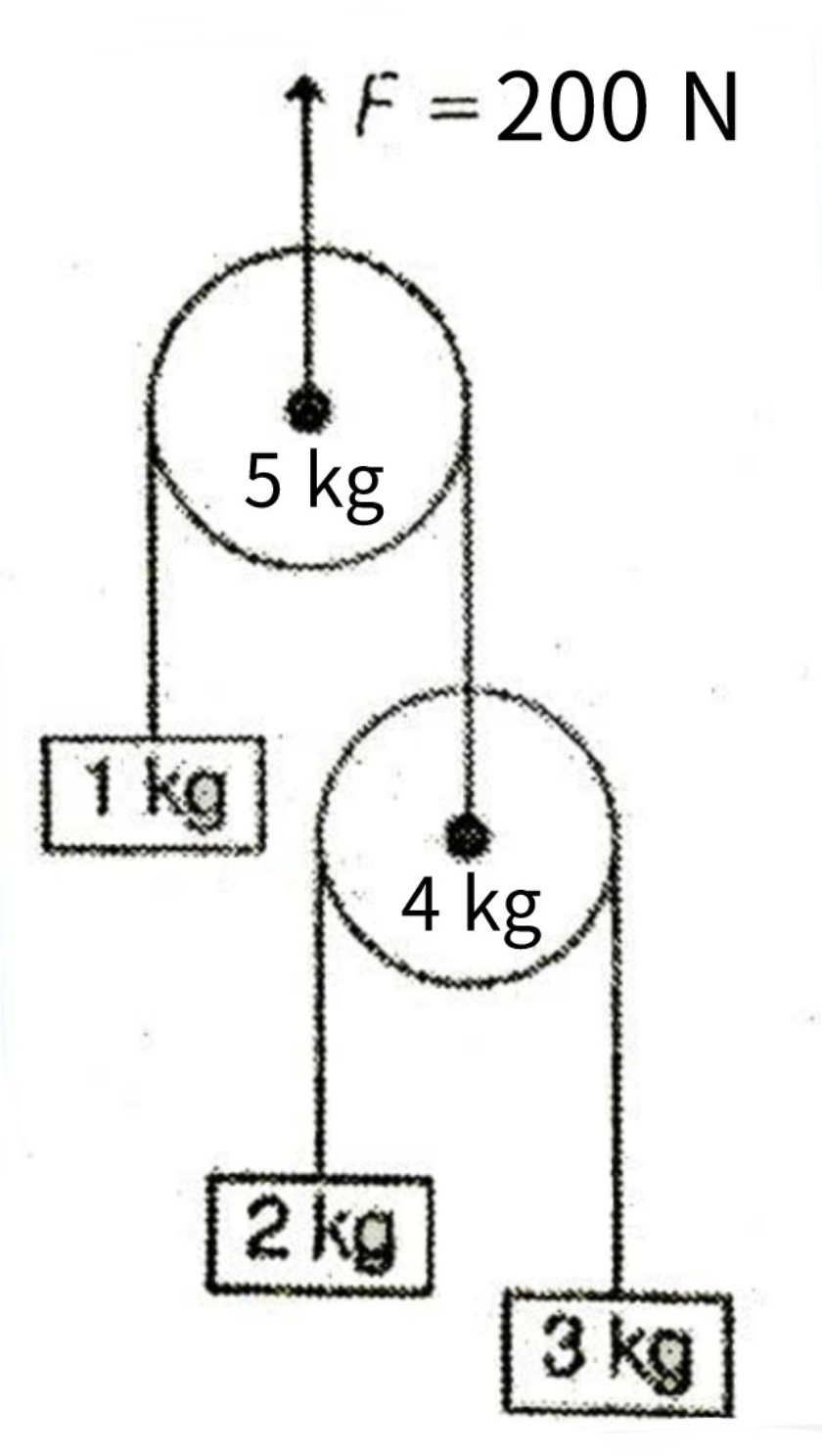
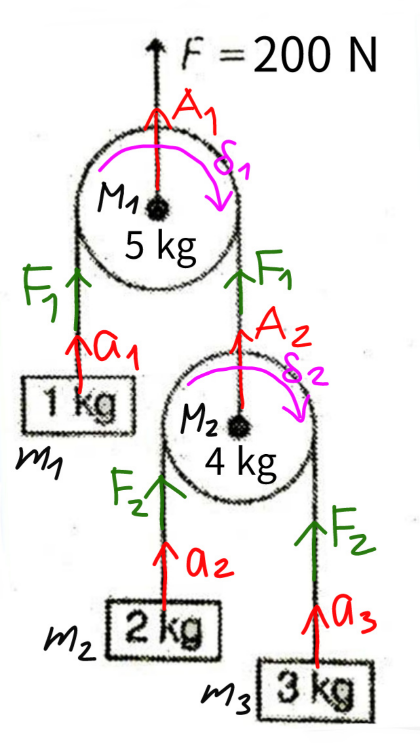
$${the}\:{strings}\:{are}\:{massless}\:{and}\:{there} \\ $$$${is}\:{no}\:{friction}\:{between}\:{strings}\:{and} \\ $$$${pulleys}. \\ $$$${find}\:{the}\:{accelerations}\:{of}\:{all}\:{objects}. \\ $$

Answered by ajfour last updated on 16/Mar/25

Acc. of 5kg block be A. relative to 4kg pulley let acc. of 3kg be a_1 ↓ and that acc. of 4kg block itself be a↓ relative to 5kg block. 3g−T_1 =3(A+a+a_1 ) ...(i) T_1 −2g=2(A+a−a_1 ) ...(ii) T_2 −g=A+a ....(iii) 2T_2 −T_1 =4(a−A) ...(iv) 200−2T_1 =5A ...(v) .................. 4(A+a+g)−2T_1 =8(a−A) 200−2T_1 =5A ⇒ 200−4(A+a+g)=13A−8a ..(1) addingr (i)&(ii) g=5A+5a+a_1 ....(2) uding (ii) in (v) 200−4g−4(A+a−a_1 )=5A ⇒ 200−4g=9A+4a−4a_1 now using (2) 200−4g=9A+4a−4(g−5A−5a) ⇒ 200=29A+24a from (1) {200−4g=17A−4a}×6 1200−24g=102A−24a 200=29A+24a adding above two 1400−24g=131A A=((1400−24g)/(131)) rest can be found now.

$${Acc}.\:{of}\:\mathrm{5}{kg}\:{block}\:{be}\:{A}. \\ $$$${relative}\:{to}\:\mathrm{4}{kg}\:{pulley}\:{let}\:{acc}.\:{of}\:\mathrm{3}{kg}\:{be}\:{a}_{\mathrm{1}} \downarrow \\ $$$${and}\:{that}\:{acc}.\:{of}\:\mathrm{4}{kg}\:{block}\:{itself}\:{be}\:{a}\downarrow\:{relative} \\ $$$${to}\:\mathrm{5}{kg}\:{block}. \\ $$$$\mathrm{3}{g}−{T}_{\mathrm{1}} =\mathrm{3}\left({A}+{a}+{a}_{\mathrm{1}} \right)\:\:\:\:...\left({i}\right) \\ $$$${T}_{\mathrm{1}} −\mathrm{2}{g}=\mathrm{2}\left({A}+{a}−{a}_{\mathrm{1}} \right)\:\:...\left({ii}\right) \\ $$$${T}_{\mathrm{2}} −{g}={A}+{a}\:\:\:\:\:\:....\left({iii}\right) \\ $$$$\mathrm{2}{T}_{\mathrm{2}} −{T}_{\mathrm{1}} =\mathrm{4}\left({a}−{A}\right)\:\:\:\:...\left({iv}\right) \\ $$$$\mathrm{200}−\mathrm{2}{T}_{\mathrm{1}} =\mathrm{5}{A}\:\:\:\:\:...\left({v}\right) \\ $$$$.................. \\ $$$$\mathrm{4}\left({A}+{a}+{g}\right)−\mathrm{2}{T}_{\mathrm{1}} =\mathrm{8}\left({a}−{A}\right) \\ $$$$\mathrm{200}−\mathrm{2}{T}_{\mathrm{1}} =\mathrm{5}{A} \\ $$$$\Rightarrow\:\:\mathrm{200}−\mathrm{4}\left({A}+{a}+{g}\right)=\mathrm{13}{A}−\mathrm{8}{a}\:\:..\left(\mathrm{1}\right) \\ $$$${addingr}\:\left({i}\right)\&\left({ii}\right) \\ $$$${g}=\mathrm{5}{A}+\mathrm{5}{a}+{a}_{\mathrm{1}} \:\:\:....\left(\mathrm{2}\right) \\ $$$${uding}\:\left({ii}\right)\:{in}\:\left({v}\right) \\ $$$$\mathrm{200}−\mathrm{4}{g}−\mathrm{4}\left({A}+{a}−{a}_{\mathrm{1}} \right)=\mathrm{5}{A} \\ $$$$\Rightarrow\:\mathrm{200}−\mathrm{4}{g}=\mathrm{9}{A}+\mathrm{4}{a}−\mathrm{4}{a}_{\mathrm{1}} \\ $$$${now}\:{using}\:\left(\mathrm{2}\right) \\ $$$$\mathrm{200}−\mathrm{4}{g}=\mathrm{9}{A}+\mathrm{4}{a}−\mathrm{4}\left({g}−\mathrm{5}{A}−\mathrm{5}{a}\right) \\ $$$$\Rightarrow\:\mathrm{200}=\mathrm{29}{A}+\mathrm{24}{a} \\ $$$${from}\:\left(\mathrm{1}\right) \\ $$$$\left\{\mathrm{200}−\mathrm{4}{g}=\mathrm{17}{A}−\mathrm{4}{a}\right\}×\mathrm{6} \\ $$$$\mathrm{1200}−\mathrm{24}{g}=\mathrm{102}{A}−\mathrm{24}{a} \\ $$$$\mathrm{200}=\mathrm{29}{A}+\mathrm{24}{a} \\ $$$${adding}\:{above}\:{two} \\ $$$$\mathrm{1400}−\mathrm{24}{g}=\mathrm{131}{A} \\ $$$${A}=\frac{\mathrm{1400}−\mathrm{24}{g}}{\mathrm{131}} \\ $$$${rest}\:{can}\:{be}\:{found}\:{now}. \\ $$

Commented by mr W last updated on 17/Mar/25

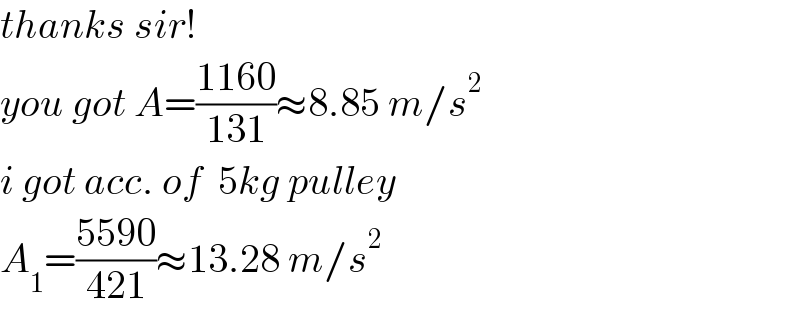
thanks sir! you got A=((1160)/(131))≈8.85 m/s^2 i got acc. of 5kg pulley A_1 =((5590)/(421))≈13.28 m/s^2

$${thanks}\:{sir}! \\ $$$${you}\:{got}\:{A}=\frac{\mathrm{1160}}{\mathrm{131}}\approx\mathrm{8}.\mathrm{85}\:{m}/{s}^{\mathrm{2}} \\ $$$${i}\:{got}\:{acc}.\:{of}\:\:\mathrm{5}{kg}\:{pulley}\: \\ $$$${A}_{\mathrm{1}} =\frac{\mathrm{5590}}{\mathrm{421}}\approx\mathrm{13}.\mathrm{28}\:{m}/{s}^{\mathrm{2}} \\ $$

Commented by ajfour last updated on 18/Mar/25

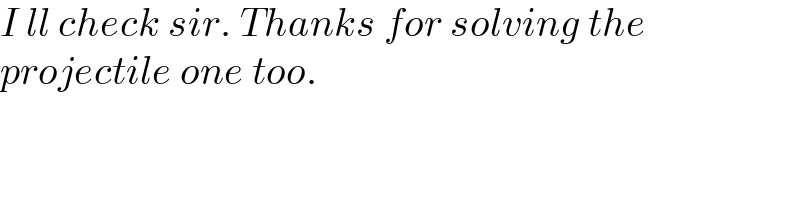
I ll check sir. Thanks for solving the projectile one too.

$${I}\:{ll}\:{check}\:{sir}.\:{Thanks}\:{for}\:{solving}\:{the} \\ $$$${projectile}\:{one}\:{too}. \\ $$

Commented by Tawa11 last updated on 21/Mar/25

That first line of this solution shouldn't it be (a + a₁) - A instead of a + a₁ +A

$$ \\ $$That first line of this solution shouldn't it be (a + a₁) - A instead of a + a₁ +A

Commented by mr W last updated on 21/Mar/25

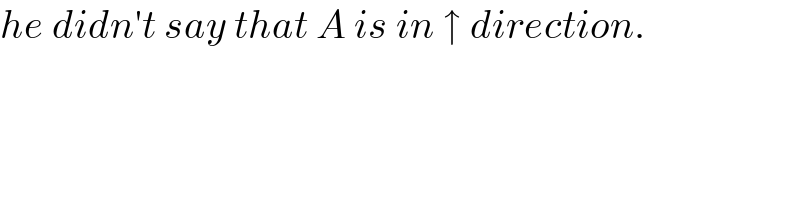
he didn′t say that A is in ↑ direction.

$${he}\:{didn}'{t}\:{say}\:{that}\:{A}\:{is}\:{in}\:\uparrow\:{direction}. \\ $$

Commented by Tawa11 last updated on 22/Mar/25

Thanks sir.

$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$

Commented by Tawa11 last updated on 22/Mar/25

Sir, help me see to Q217797 That differential equation.

$$\mathrm{Sir},\:\mathrm{help}\:\mathrm{me}\:\mathrm{see}\:\mathrm{to}\:\mathrm{Q217797} \\ $$$$\mathrm{That}\:\mathrm{differential}\:\mathrm{equation}. \\ $$

Answered by mr W last updated on 17/Mar/25

Commented by mr W last updated on 17/Mar/25

δ_1 relative acc. of string to pulley 1 δ_2 relative acc. of string to pulley 2 a_1 =A_1 +δ_1 A_2 =A_1 −δ_1 a_2 =A_2 +δ_2 =A_1 −δ_1 +δ_2 a_3 =A_2 −δ_2 =A_1 −δ_1 −δ_2 F_2 =m_2 (g+a_2 )=m_2 (g+A_1 −δ_1 +δ_2 ) F_2 =m_3 (g+a_3 )=m_3 (g+A_1 −δ_1 −δ_2 ) F_1 =m_1 (g+a_1 )=m_1 (g+A_1 +δ_1 ) F_1 −2F_2 =M_2 (g+A_2 )=M_2 (g+A_1 −δ_1 ) F−2F_1 =M_1 (g+A_1 ) F−2m_1 (g+A_1 +δ_1 )=M_1 (g+A_1 ) (M_1 +2m_1 )A_1 +2m_1 δ_1 =F−(M_1 +2m_1 )g 7A_1 +2δ_1 =130 ...(i) m_1 (g+A_1 +δ_1 )−2m_2 (g+A_1 −δ_1 +δ_2 )=M_2 (g+A_1 −δ_1 ) (m_1 −2m_2 −M_2 )A_1 +(M_2 +m_1 +2m_2 )δ_1 −2m_2 δ_2 =(M_2 −m_1 +2m_2 )g −7A_1 +9δ_1 −4δ_2 =70 ...(ii) m_2 (g+A_1 −δ_1 +δ_2 )=m_3 (g+A_1 −δ_1 −δ_2 ) (m_2 −m_3 )A_1 +(−m_2 +m_3 )δ_1 +(m_2 +m_3 )δ_2 =(m_3 −m_2 )g −A_1 +δ_1 +5δ_2 =10 ...(iii) δ_1 =((7800)/(421)) δ_2 =((400)/(421)) A_1 =((7800)/(421))+5×((400)/(421))−10=((5590)/(421)) A_2 =((5590)/(421))−((7800)/(421))=−((2210)/(421)) a_1 =((5590)/(421))+((7800)/(421))=((13390)/(421)) a_2 =−((2210)/(421))+((400)/(421))=−((1810)/(421)) a_3 =−((2210)/(421))−((400)/(421))=−((2610)/(421))

$$\delta_{\mathrm{1}} \:{relative}\:{acc}.\:{of}\:{string}\:{to}\:{pulley}\:\mathrm{1} \\ $$$$\delta_{\mathrm{2}} \:{relative}\:{acc}.\:{of}\:{string}\:{to}\:{pulley}\:\mathrm{2} \\ $$$${a}_{\mathrm{1}} ={A}_{\mathrm{1}} +\delta_{\mathrm{1}} \\ $$$${A}_{\mathrm{2}} ={A}_{\mathrm{1}} −\delta_{\mathrm{1}} \\ $$$${a}_{\mathrm{2}} ={A}_{\mathrm{2}} +\delta_{\mathrm{2}} ={A}_{\mathrm{1}} −\delta_{\mathrm{1}} +\delta_{\mathrm{2}} \\ $$$${a}_{\mathrm{3}} ={A}_{\mathrm{2}} −\delta_{\mathrm{2}} ={A}_{\mathrm{1}} −\delta_{\mathrm{1}} −\delta_{\mathrm{2}} \\ $$$$ \\ $$$${F}_{\mathrm{2}} ={m}_{\mathrm{2}} \left({g}+{a}_{\mathrm{2}} \right)={m}_{\mathrm{2}} \left({g}+{A}_{\mathrm{1}} −\delta_{\mathrm{1}} +\delta_{\mathrm{2}} \right) \\ $$$${F}_{\mathrm{2}} ={m}_{\mathrm{3}} \left({g}+{a}_{\mathrm{3}} \right)={m}_{\mathrm{3}} \left({g}+{A}_{\mathrm{1}} −\delta_{\mathrm{1}} −\delta_{\mathrm{2}} \right) \\ $$$${F}_{\mathrm{1}} ={m}_{\mathrm{1}} \left({g}+{a}_{\mathrm{1}} \right)={m}_{\mathrm{1}} \left({g}+{A}_{\mathrm{1}} +\delta_{\mathrm{1}} \right) \\ $$$${F}_{\mathrm{1}} −\mathrm{2}{F}_{\mathrm{2}} ={M}_{\mathrm{2}} \left({g}+{A}_{\mathrm{2}} \right)={M}_{\mathrm{2}} \left({g}+{A}_{\mathrm{1}} −\delta_{\mathrm{1}} \right) \\ $$$${F}−\mathrm{2}{F}_{\mathrm{1}} ={M}_{\mathrm{1}} \left({g}+{A}_{\mathrm{1}} \right) \\ $$$$ \\ $$$${F}−\mathrm{2}{m}_{\mathrm{1}} \left({g}+{A}_{\mathrm{1}} +\delta_{\mathrm{1}} \right)={M}_{\mathrm{1}} \left({g}+{A}_{\mathrm{1}} \right) \\ $$$$\left({M}_{\mathrm{1}} +\mathrm{2}{m}_{\mathrm{1}} \right){A}_{\mathrm{1}} +\mathrm{2}{m}_{\mathrm{1}} \delta_{\mathrm{1}} ={F}−\left({M}_{\mathrm{1}} +\mathrm{2}{m}_{\mathrm{1}} \right){g} \\ $$$$\mathrm{7}{A}_{\mathrm{1}} +\mathrm{2}\delta_{\mathrm{1}} =\mathrm{130}\:\:\:...\left({i}\right) \\ $$$$ \\ $$$${m}_{\mathrm{1}} \left({g}+{A}_{\mathrm{1}} +\delta_{\mathrm{1}} \right)−\mathrm{2}{m}_{\mathrm{2}} \left({g}+{A}_{\mathrm{1}} −\delta_{\mathrm{1}} +\delta_{\mathrm{2}} \right)={M}_{\mathrm{2}} \left({g}+{A}_{\mathrm{1}} −\delta_{\mathrm{1}} \right) \\ $$$$\left({m}_{\mathrm{1}} −\mathrm{2}{m}_{\mathrm{2}} −{M}_{\mathrm{2}} \right){A}_{\mathrm{1}} +\left({M}_{\mathrm{2}} +{m}_{\mathrm{1}} +\mathrm{2}{m}_{\mathrm{2}} \right)\delta_{\mathrm{1}} −\mathrm{2}{m}_{\mathrm{2}} \delta_{\mathrm{2}} =\left({M}_{\mathrm{2}} −{m}_{\mathrm{1}} +\mathrm{2}{m}_{\mathrm{2}} \right){g} \\ $$$$−\mathrm{7}{A}_{\mathrm{1}} +\mathrm{9}\delta_{\mathrm{1}} −\mathrm{4}\delta_{\mathrm{2}} =\mathrm{70}\:\:\:...\left({ii}\right) \\ $$$$ \\ $$$${m}_{\mathrm{2}} \left({g}+{A}_{\mathrm{1}} −\delta_{\mathrm{1}} +\delta_{\mathrm{2}} \right)={m}_{\mathrm{3}} \left({g}+{A}_{\mathrm{1}} −\delta_{\mathrm{1}} −\delta_{\mathrm{2}} \right) \\ $$$$\left({m}_{\mathrm{2}} −{m}_{\mathrm{3}} \right){A}_{\mathrm{1}} +\left(−{m}_{\mathrm{2}} +{m}_{\mathrm{3}} \right)\delta_{\mathrm{1}} +\left({m}_{\mathrm{2}} +{m}_{\mathrm{3}} \right)\delta_{\mathrm{2}} =\left({m}_{\mathrm{3}} −{m}_{\mathrm{2}} \right){g} \\ $$$$−{A}_{\mathrm{1}} +\delta_{\mathrm{1}} +\mathrm{5}\delta_{\mathrm{2}} =\mathrm{10}\:\:\:...\left({iii}\right) \\ $$$$ \\ $$$$\delta_{\mathrm{1}} =\frac{\mathrm{7800}}{\mathrm{421}} \\ $$$$\delta_{\mathrm{2}} =\frac{\mathrm{400}}{\mathrm{421}} \\ $$$${A}_{\mathrm{1}} =\frac{\mathrm{7800}}{\mathrm{421}}+\mathrm{5}×\frac{\mathrm{400}}{\mathrm{421}}−\mathrm{10}=\frac{\mathrm{5590}}{\mathrm{421}} \\ $$$$ \\ $$$${A}_{\mathrm{2}} =\frac{\mathrm{5590}}{\mathrm{421}}−\frac{\mathrm{7800}}{\mathrm{421}}=−\frac{\mathrm{2210}}{\mathrm{421}} \\ $$$${a}_{\mathrm{1}} =\frac{\mathrm{5590}}{\mathrm{421}}+\frac{\mathrm{7800}}{\mathrm{421}}=\frac{\mathrm{13390}}{\mathrm{421}} \\ $$$${a}_{\mathrm{2}} =−\frac{\mathrm{2210}}{\mathrm{421}}+\frac{\mathrm{400}}{\mathrm{421}}=−\frac{\mathrm{1810}}{\mathrm{421}} \\ $$$${a}_{\mathrm{3}} =−\frac{\mathrm{2210}}{\mathrm{421}}−\frac{\mathrm{400}}{\mathrm{421}}=−\frac{\mathrm{2610}}{\mathrm{421}} \\ $$

Commented by Tawa11 last updated on 18/Mar/25

Sir, you assumed the cylinder are rotating here. But Ajfour did not assume the cylinder is rotating.

$$\mathrm{Sir},\:\mathrm{you}\:\mathrm{assumed}\:\mathrm{the}\:\mathrm{cylinder}\:\mathrm{are}\:\mathrm{rotating}\:\mathrm{here}. \\ $$$$\mathrm{But}\:\mathrm{Ajfour}\:\mathrm{did}\:\mathrm{not}\:\mathrm{assume}\:\mathrm{the}\:\mathrm{cylinder}\:\mathrm{is}\:\mathrm{rotating}. \\ $$

Commented by mr W last updated on 18/Mar/25

The pulleys don′t rotate and i also didn′t assume that they rotate.

$${The}\:{pulleys}\:{don}'{t}\:{rotate}\:{and}\:{i}\:{also} \\ $$$${didn}'{t}\:{assume}\:{that}\:{they}\:{rotate}. \\ $$

Commented by Tawa11 last updated on 18/Mar/25

Thanks sir.

$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$

Commented by mr W last updated on 18/Mar/25

if there is no friction between string and pulley, the string can also move relatively to the pulley without that the pulley rotates. in the workings above δ_1 and δ_2 are the relative motions of the strings along the pulleys. there are not the rotation of the pulleys!

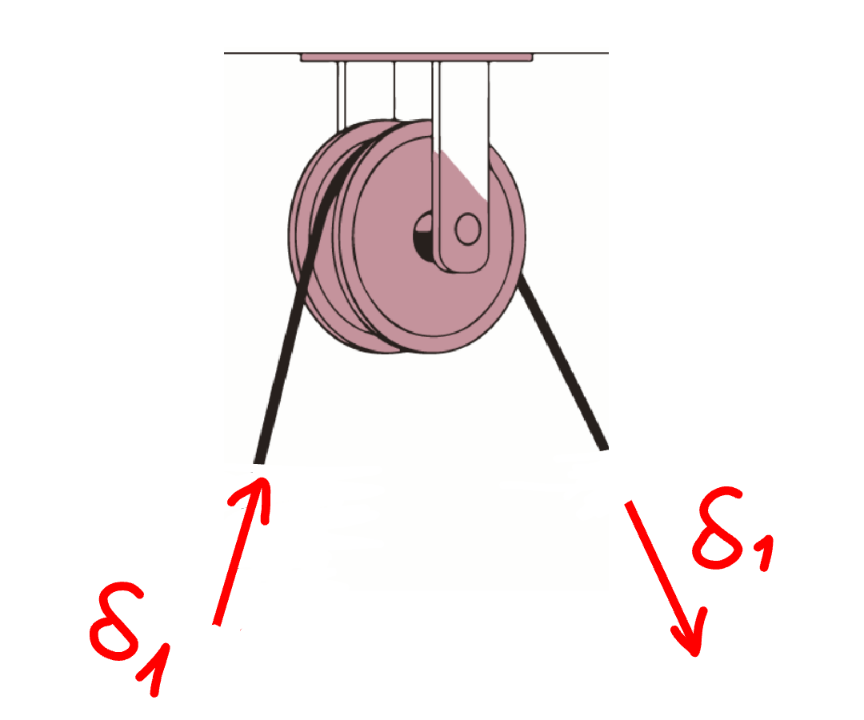
$${if}\:{there}\:{is}\:{no}\:{friction}\:{between}\:{string} \\ $$$${and}\:{pulley},\:{the}\:{string}\:{can}\:{also}\: \\ $$$${move}\:{relatively}\:{to}\:{the}\:{pulley}\:{without} \\ $$$${that}\:{the}\:{pulley}\:{rotates}. \\ $$$${in}\:{the}\:{workings}\:{above}\:\delta_{\mathrm{1}} \:{and}\:\delta_{\mathrm{2}} \:{are} \\ $$$${the}\:{relative}\:{motions}\:{of}\:{the}\:{strings} \\ $$$${along}\:{the}\:{pulleys}.\:{there}\:{are}\:{not}\:{the} \\ $$$${rotation}\:{of}\:{the}\:{pulleys}! \\ $$

Commented by mr W last updated on 18/Mar/25

Commented by Tawa11 last updated on 18/Mar/25

Ohh, thanks sir. I appreciate your time.

$$\mathrm{Ohh},\:\mathrm{thanks}\:\mathrm{sir}. \\ $$$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{time}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com