Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 217506 by Tawa11 last updated on 15/Mar/25

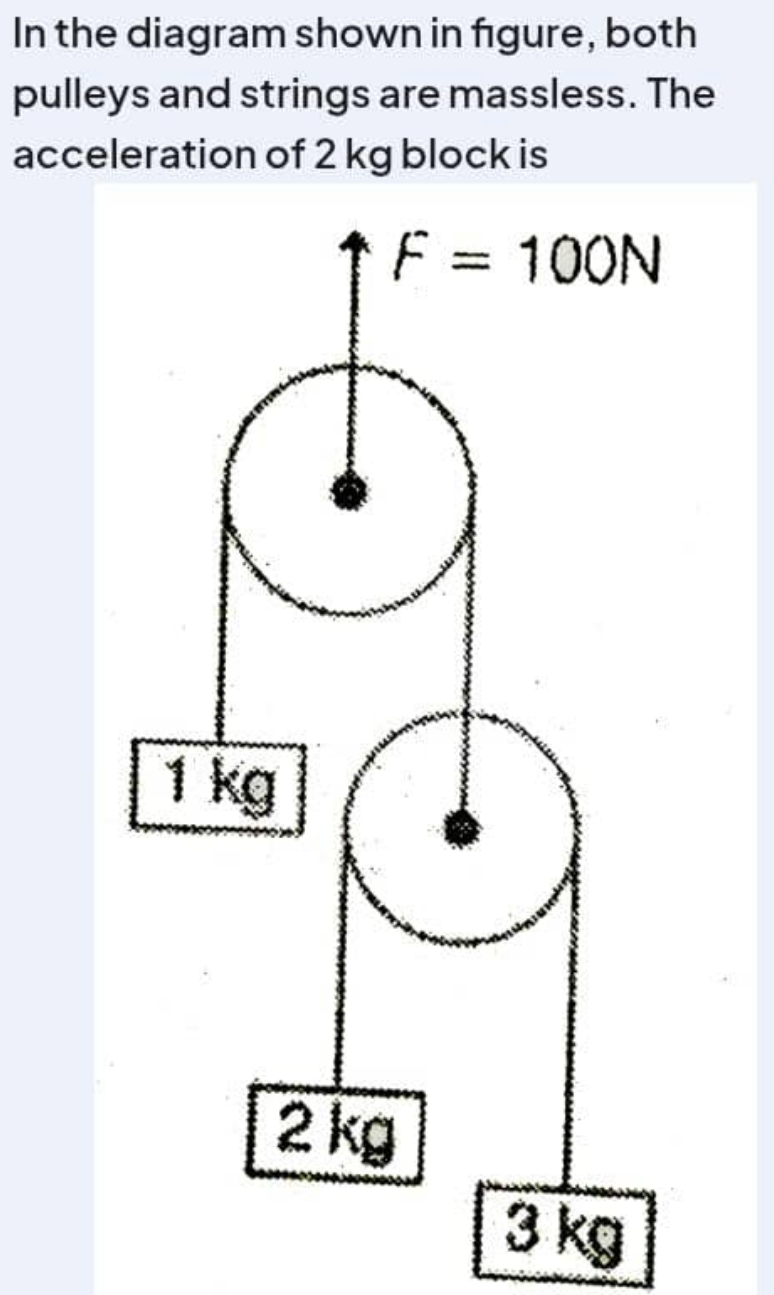
Commented by Tawa11 last updated on 15/Mar/25

2.5m/s^2 ?

$$\mathrm{2}.\mathrm{5m}/\mathrm{s}^{\mathrm{2}} \:? \\ $$

Commented by mr W last updated on 15/Mar/25

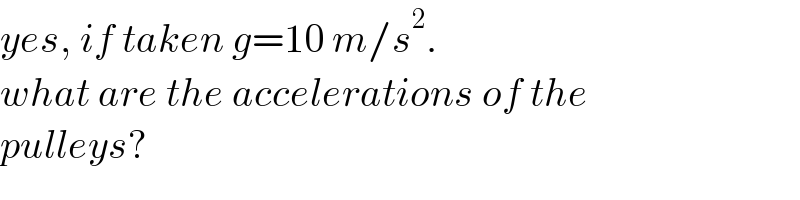
yes, if taken g=10 m/s^2 . what are the accelerations of the pulleys?

$${yes},\:{if}\:{taken}\:{g}=\mathrm{10}\:{m}/{s}^{\mathrm{2}} . \\ $$$${what}\:{are}\:{the}\:{accelerations}\:{of}\:{the} \\ $$$${pulleys}? \\ $$

Commented by Tawa11 last updated on 15/Mar/25

Sir, I only solve acceleration of the block. Show me the acceleration of pulleys sir.

$$\mathrm{Sir},\:\mathrm{I}\:\mathrm{only}\:\mathrm{solve}\:\mathrm{acceleration}\:\mathrm{of}\:\mathrm{the}\:\mathrm{block}. \\ $$$$\mathrm{Show}\:\mathrm{me}\:\mathrm{the}\:\mathrm{acceleration}\:\mathrm{of}\:\mathrm{pulleys}\:\mathrm{sir}. \\ $$

Commented by Tawa11 last updated on 15/Mar/25

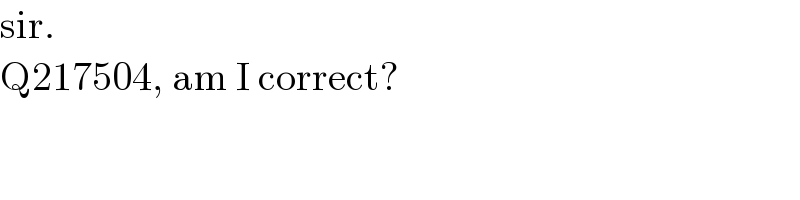
sir. Q217504, am I correct?

$$\mathrm{sir}. \\ $$$$\mathrm{Q217504},\:\mathrm{am}\:\mathrm{I}\:\mathrm{correct}? \\ $$

Commented by mr W last updated on 15/Mar/25

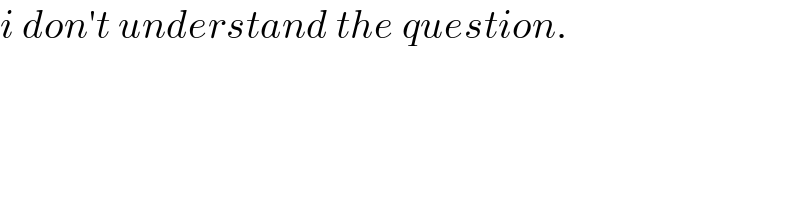
i don′t understand the question.

$${i}\:{don}'{t}\:{understand}\:{the}\:{question}. \\ $$

Commented by Tawa11 last updated on 15/Mar/25

Hahahahahaha. I think the question is missing a parameter.

$$\mathrm{Hahahahahaha}. \\ $$$$\mathrm{I}\:\mathrm{think}\:\mathrm{the}\:\mathrm{question}\:\mathrm{is}\:\mathrm{missing}\:\mathrm{a} \\ $$$$\mathrm{parameter}. \\ $$

Commented by Tawa11 last updated on 15/Mar/25

Thanks sir.

$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$

Answered by mr W last updated on 15/Mar/25

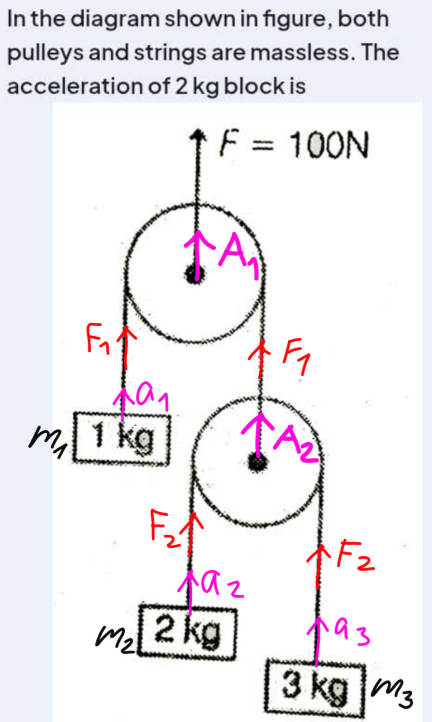
Commented by mr W last updated on 15/Mar/25

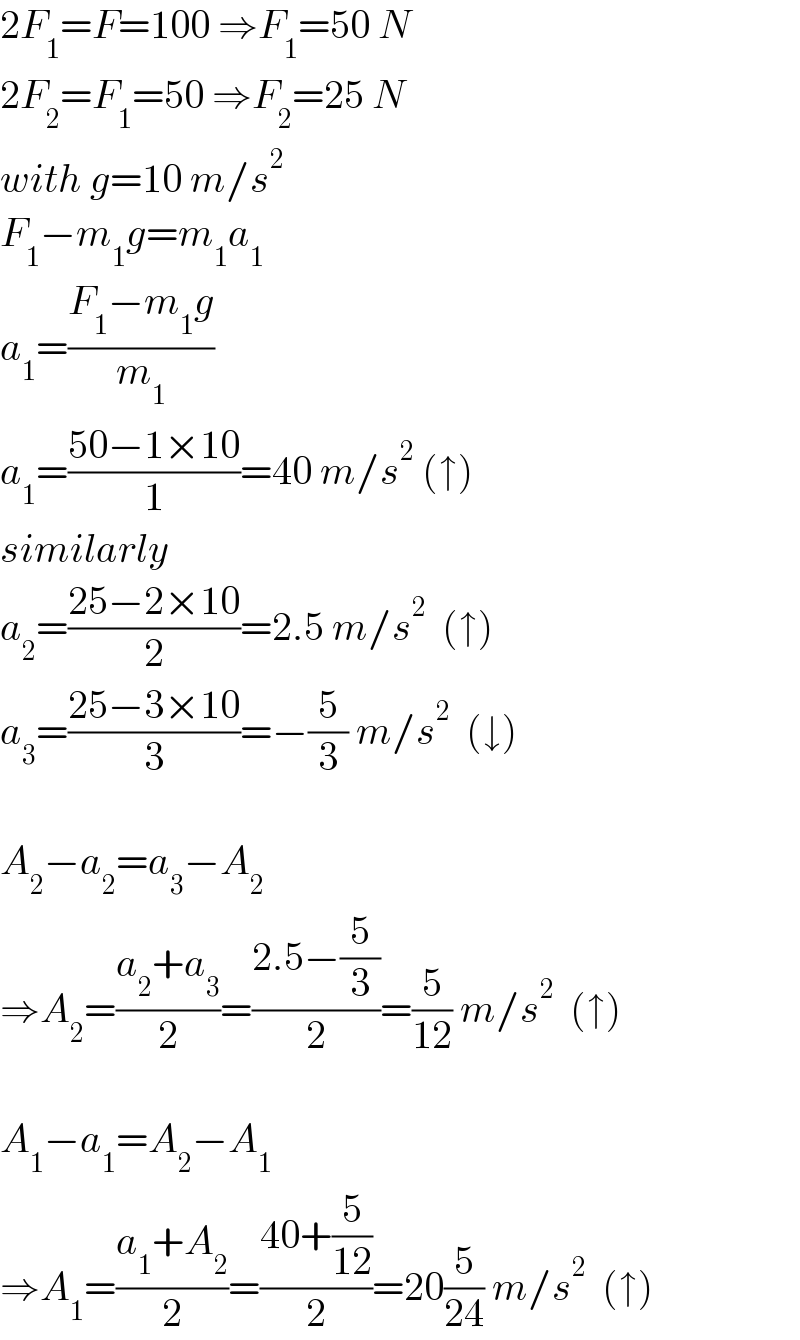
2F_1 =F=100 ⇒F_1 =50 N 2F_2 =F_1 =50 ⇒F_2 =25 N with g=10 m/s^2 F_1 −m_1 g=m_1 a_1 a_1 =((F_1 −m_1 g)/m_1 ) a_1 =((50−1×10)/1)=40 m/s^2 (↑) similarly a_2 =((25−2×10)/2)=2.5 m/s^2 (↑) a_3 =((25−3×10)/3)=−(5/3) m/s^2 (↓) A_2 −a_2 =a_3 −A_2 ⇒A_2 =((a_2 +a_3 )/2)=((2.5−(5/3))/2)=(5/(12)) m/s^2 (↑) A_1 −a_1 =A_2 −A_1 ⇒A_1 =((a_1 +A_2 )/2)=((40+(5/(12)))/2)=20(5/(24)) m/s^2 (↑)

$$\mathrm{2}{F}_{\mathrm{1}} ={F}=\mathrm{100}\:\Rightarrow{F}_{\mathrm{1}} =\mathrm{50}\:{N} \\ $$$$\mathrm{2}{F}_{\mathrm{2}} ={F}_{\mathrm{1}} =\mathrm{50}\:\Rightarrow{F}_{\mathrm{2}} =\mathrm{25}\:{N} \\ $$$${with}\:{g}=\mathrm{10}\:{m}/{s}^{\mathrm{2}} \\ $$$${F}_{\mathrm{1}} −{m}_{\mathrm{1}} {g}={m}_{\mathrm{1}} {a}_{\mathrm{1}} \\ $$$${a}_{\mathrm{1}} =\frac{{F}_{\mathrm{1}} −{m}_{\mathrm{1}} {g}}{{m}_{\mathrm{1}} } \\ $$$${a}_{\mathrm{1}} =\frac{\mathrm{50}−\mathrm{1}×\mathrm{10}}{\mathrm{1}}=\mathrm{40}\:{m}/{s}^{\mathrm{2}} \:\left(\uparrow\right) \\ $$$${similarly} \\ $$$${a}_{\mathrm{2}} =\frac{\mathrm{25}−\mathrm{2}×\mathrm{10}}{\mathrm{2}}=\mathrm{2}.\mathrm{5}\:{m}/{s}^{\mathrm{2}} \:\:\left(\uparrow\right) \\ $$$${a}_{\mathrm{3}} =\frac{\mathrm{25}−\mathrm{3}×\mathrm{10}}{\mathrm{3}}=−\frac{\mathrm{5}}{\mathrm{3}}\:{m}/{s}^{\mathrm{2}} \:\:\left(\downarrow\right) \\ $$$$ \\ $$$${A}_{\mathrm{2}} −{a}_{\mathrm{2}} ={a}_{\mathrm{3}} −{A}_{\mathrm{2}} \: \\ $$$$\Rightarrow{A}_{\mathrm{2}} =\frac{{a}_{\mathrm{2}} +{a}_{\mathrm{3}} }{\mathrm{2}}=\frac{\mathrm{2}.\mathrm{5}−\frac{\mathrm{5}}{\mathrm{3}}}{\mathrm{2}}=\frac{\mathrm{5}}{\mathrm{12}}\:{m}/{s}^{\mathrm{2}} \:\:\left(\uparrow\right) \\ $$$$ \\ $$$${A}_{\mathrm{1}} −{a}_{\mathrm{1}} ={A}_{\mathrm{2}} −{A}_{\mathrm{1}} \\ $$$$\Rightarrow{A}_{\mathrm{1}} =\frac{{a}_{\mathrm{1}} +{A}_{\mathrm{2}} }{\mathrm{2}}=\frac{\mathrm{40}+\frac{\mathrm{5}}{\mathrm{12}}}{\mathrm{2}}=\mathrm{20}\frac{\mathrm{5}}{\mathrm{24}}\:{m}/{s}^{\mathrm{2}} \:\:\left(\uparrow\right) \\ $$

Commented by Tawa11 last updated on 15/Mar/25

God bless you sir. I really appreciate you sir.

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$$$\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Commented by Tawa11 last updated on 15/Mar/25

For mass 3kg = 5ms^(−1) For mas 2kg = 2.5 ms^(−1) for mass 1kg = 3.75ms^(−1)

$$\mathrm{For}\:\mathrm{mass}\:\mathrm{3kg}\:\:=\:\:\mathrm{5ms}^{−\mathrm{1}} \\ $$$$\mathrm{For}\:\mathrm{mas}\:\mathrm{2kg}\:\:=\:\:\mathrm{2}.\mathrm{5}\:\mathrm{ms}^{−\mathrm{1}} \\ $$$$\mathrm{for}\:\mathrm{mass}\:\mathrm{1kg}\:\:=\:\:\mathrm{3}.\mathrm{75ms}^{−\mathrm{1}} \\ $$

Commented by mr W last updated on 15/Mar/25

wrong!

$${wrong}! \\ $$

Commented by Tawa11 last updated on 15/Mar/25

I will try more

$$\mathrm{I}\:\mathrm{will}\:\mathrm{try}\:\mathrm{more} \\ $$

Commented by Tawa11 last updated on 16/Mar/25

1.8 ms^(− 2) is this correct sir. for the 3kg, 2kg and 1kg pulleys

$$\mathrm{1}.\mathrm{8}\:\mathrm{ms}^{−\:\mathrm{2}} \\ $$$$\mathrm{is}\:\mathrm{this}\:\mathrm{correct}\:\mathrm{sir}. \\ $$$$\mathrm{for}\:\mathrm{the}\:\mathrm{3kg},\:\mathrm{2kg}\:\mathrm{and}\:\mathrm{1kg}\:\:\mathrm{pulleys} \\ $$

Commented by mr W last updated on 16/Mar/25

no! how can they all have the same acceleration? they are not fixed with each other.

$${no}!\:{how}\:{can}\:{they}\:{all}\:{have}\:{the}\:{same} \\ $$$${acceleration}?\:{they}\:{are}\:{not}\:{fixed} \\ $$$${with}\:{each}\:{other}. \\ $$

Commented by Tawa11 last updated on 16/Mar/25

noted sir.

$$\mathrm{noted}\:\mathrm{sir}. \\ $$

Commented by Tawa11 last updated on 16/Mar/25

Please solve sir.

$$\mathrm{Please}\:\mathrm{solve}\:\mathrm{sir}. \\ $$

Commented by mr W last updated on 16/Mar/25

i have given an example above. if you have understood this, i think you should be able to solve it by yourself. but i have opened a new thread. you can follow the question and solution there.

$${i}\:{have}\:{given}\:{an}\:{example}\:{above}.\:{if} \\ $$$${you}\:{have}\:{understood}\:{this},\:{i}\:{think}\: \\ $$$${you}\:{should}\:{be}\:{able}\:{to}\:{solve}\:{it}\:{by} \\ $$$${yourself}.\:{but}\:{i}\:{have}\:{opened}\:{a}\:{new} \\ $$$${thread}.\:{you}\:{can}\:{follow}\:{the}\:{question} \\ $$$${and}\:{solution}\:{there}. \\ $$

Commented by Tawa11 last updated on 16/Mar/25

you have not solve Q217565 sir

$$\mathrm{you}\:\mathrm{have}\:\mathrm{not}\:\mathrm{solve}\:\mathrm{Q217565}\:\mathrm{sir} \\ $$

Commented by mr W last updated on 16/Mar/25

i know. but it is solved! you can compare with your own solution.

$${i}\:{know}.\:{but}\:{it}\:{is}\:{solved}!\:{you}\:{can}\: \\ $$$${compare}\:{with}\:{your}\:{own}\:{solution}. \\ $$

Commented by Tawa11 last updated on 16/Mar/25

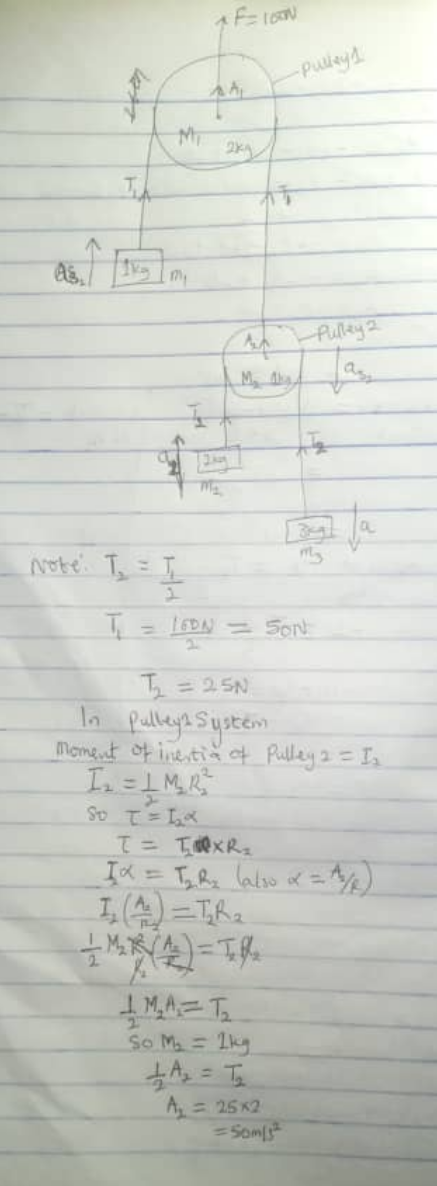
Commented by Tawa11 last updated on 16/Mar/25

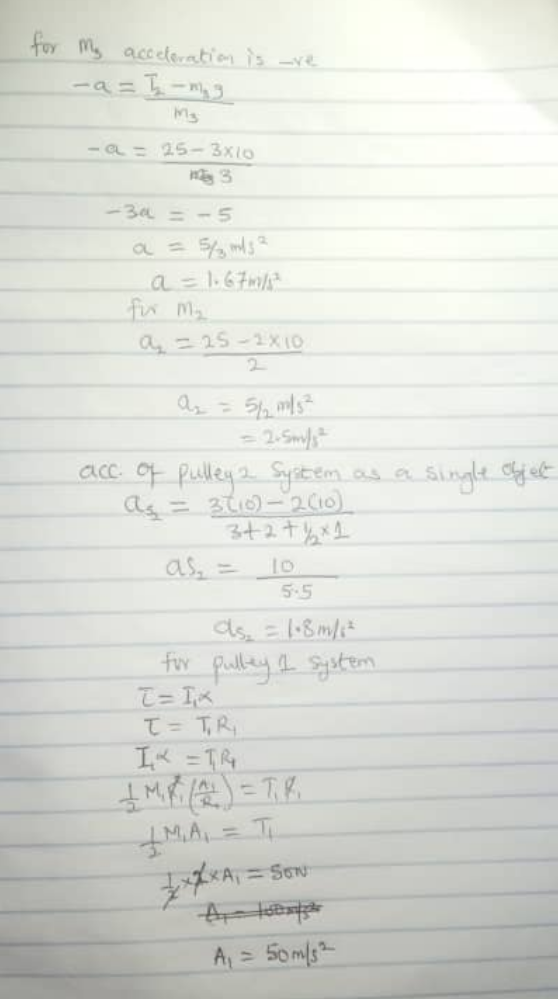
Commented by Tawa11 last updated on 16/Mar/25

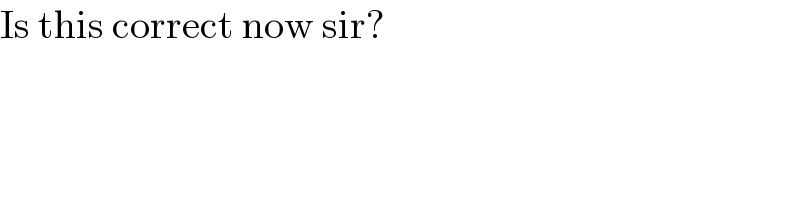
Is this correct now sir?

$$\mathrm{Is}\:\mathrm{this}\:\mathrm{correct}\:\mathrm{now}\:\mathrm{sir}? \\ $$

Commented by mr W last updated on 17/Mar/25

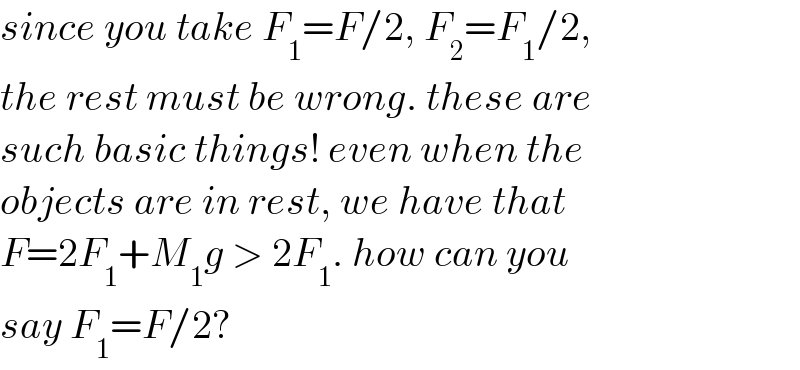
since you take F_1 =F/2, F_2 =F_1 /2, the rest must be wrong. these are such basic things! even when the objects are in rest, we have that F=2F_1 +M_1 g > 2F_1 . how can you say F_1 =F/2?

$${since}\:{you}\:{take}\:{F}_{\mathrm{1}} ={F}/\mathrm{2},\:{F}_{\mathrm{2}} ={F}_{\mathrm{1}} /\mathrm{2},\: \\ $$$${the}\:{rest}\:{must}\:{be}\:{wrong}.\:{these}\:{are}\: \\ $$$${such}\:{basic}\:{things}!\:{even}\:{when}\:{the}\: \\ $$$${objects}\:{are}\:{in}\:{rest},\:{we}\:{have}\:{that} \\ $$$${F}=\mathrm{2}{F}_{\mathrm{1}} +{M}_{\mathrm{1}} {g}\:>\:\mathrm{2}{F}_{\mathrm{1}} .\:{how}\:{can}\:{you}\: \\ $$$${say}\:{F}_{\mathrm{1}} ={F}/\mathrm{2}? \\ $$

Commented by mr W last updated on 17/Mar/25

it is assumed that there is no friction between the strings and the pulleys. in this case the pulley don′t rotate. otherwise you can not assume that the string on both sides of a pulley has the same tension, but have assumed F_(1, left) =F_(1, right) =F_1 , therefore no friction and no rotation of pulleys!

$${it}\:{is}\:{assumed}\:{that}\:{there}\:{is}\:{no} \\ $$$${friction}\:{between}\:{the}\:{strings}\:{and} \\ $$$${the}\:{pulleys}.\:{in}\:{this}\:{case}\:{the}\:{pulley} \\ $$$${don}'{t}\:{rotate}.\:{otherwise}\:{you}\:{can}\:{not} \\ $$$${assume}\:{that}\:{the}\:{string}\:{on}\:{both}\:{sides} \\ $$$${of}\:{a}\:{pulley}\:{has}\:{the}\:{same}\:{tension},\:{but} \\ $$$${have}\:{assumed}\:{F}_{\mathrm{1},\:{left}} ={F}_{\mathrm{1},\:{right}} ={F}_{\mathrm{1}} , \\ $$$${therefore}\:{no}\:{friction}\:{and}\:{no}\: \\ $$$${rotation}\:{of}\:{pulleys}! \\ $$

Commented by Tawa11 last updated on 17/Mar/25

Noted sir.

$$\mathrm{Noted}\:\mathrm{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com