Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 217495 by Hanuda354 last updated on 14/Mar/25

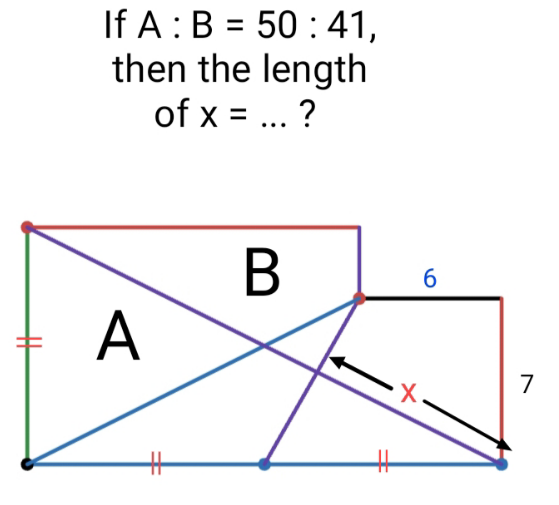
Answered by mr W last updated on 17/Mar/25

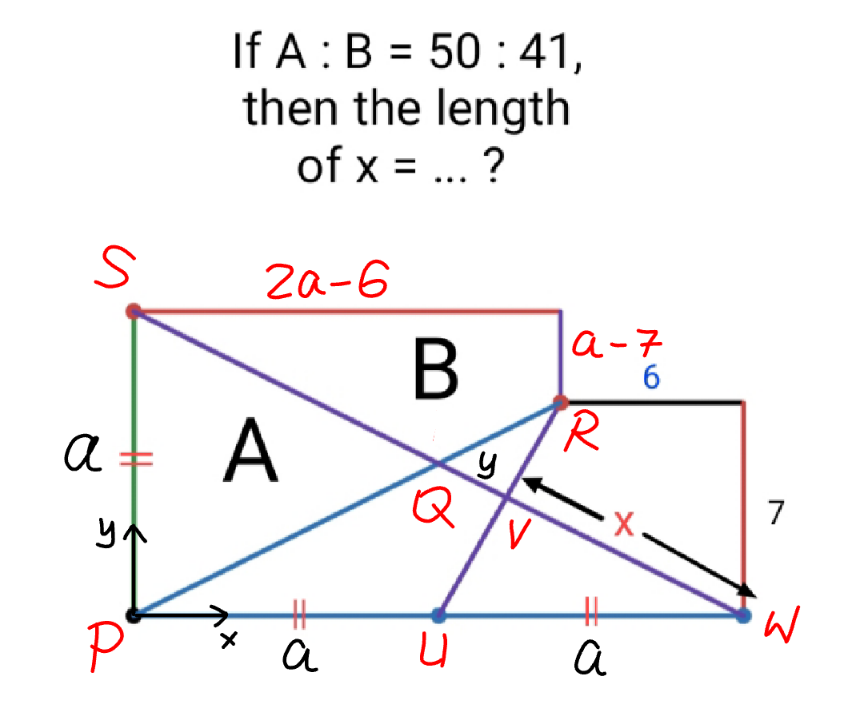
Commented by Hanuda354 last updated on 18/Mar/25

Thanks a lot, Prof.

$$\mathrm{Thanks}\:\:\mathrm{a}\:\:\mathrm{lot},\:\mathrm{Prof}. \\ $$

Commented by mr W last updated on 17/Mar/25

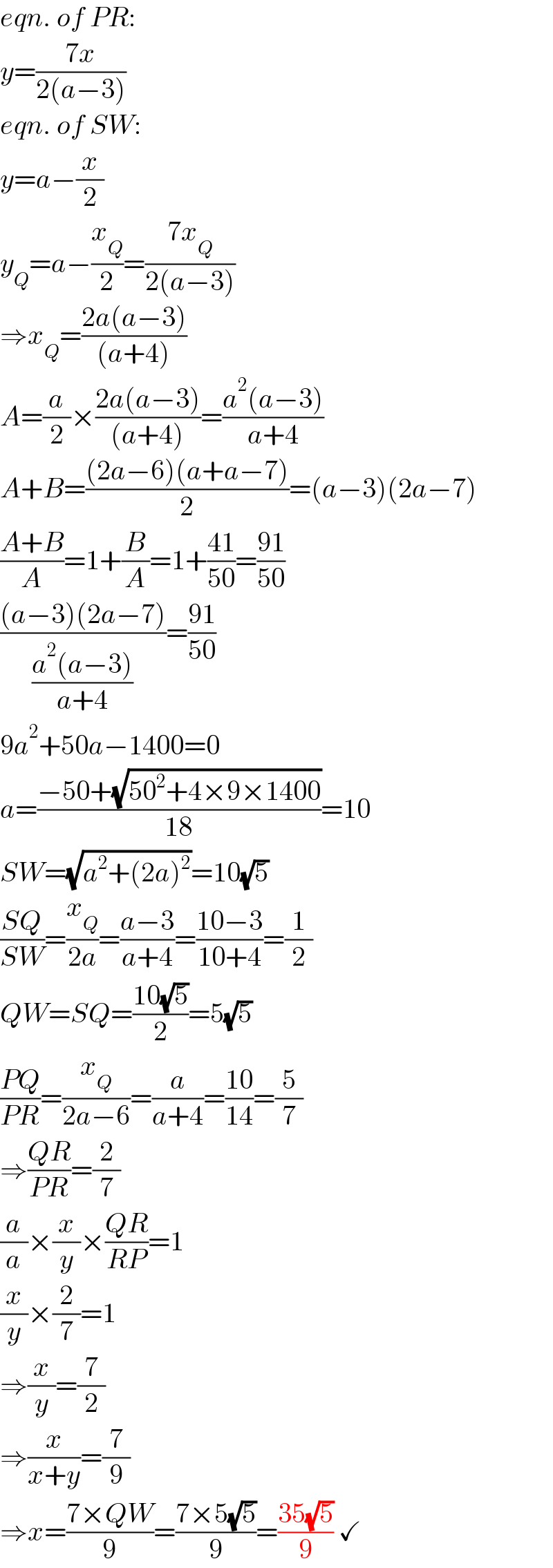
eqn. of PR: y=((7x)/(2(a−3))) eqn. of SW: y=a−(x/2) y_Q =a−(x_Q /2)=((7x_Q )/(2(a−3))) ⇒x_Q =((2a(a−3))/((a+4))) A=(a/2)×((2a(a−3))/((a+4)))=((a^2 (a−3))/(a+4)) A+B=(((2a−6)(a+a−7))/2)=(a−3)(2a−7) ((A+B)/A)=1+(B/A)=1+((41)/(50))=((91)/(50)) (((a−3)(2a−7))/((a^2 (a−3))/(a+4)))=((91)/(50)) 9a^2 +50a−1400=0 a=((−50+(√(50^2 +4×9×1400)))/(18))=10 SW=(√(a^2 +(2a)^2 ))=10(√5) ((SQ)/(SW))=(x_Q /(2a))=((a−3)/(a+4))=((10−3)/(10+4))=(1/2) QW=SQ=((10(√5))/2)=5(√5) ((PQ)/(PR))=(x_Q /(2a−6))=(a/(a+4))=((10)/(14))=(5/7) ⇒((QR)/(PR))=(2/7) (a/a)×(x/y)×((QR)/(RP))=1 (x/y)×(2/7)=1 ⇒(x/y)=(7/2) ⇒(x/(x+y))=(7/9) ⇒x=((7×QW)/9)=((7×5(√5))/9)=((35(√5))/9) ✓

$${eqn}.\:{of}\:{PR}: \\ $$$${y}=\frac{\mathrm{7}{x}}{\mathrm{2}\left({a}−\mathrm{3}\right)} \\ $$$${eqn}.\:{of}\:{SW}: \\ $$$${y}={a}−\frac{{x}}{\mathrm{2}} \\ $$$${y}_{{Q}} ={a}−\frac{{x}_{{Q}} }{\mathrm{2}}=\frac{\mathrm{7}{x}_{{Q}} }{\mathrm{2}\left({a}−\mathrm{3}\right)} \\ $$$$\Rightarrow{x}_{{Q}} =\frac{\mathrm{2}{a}\left({a}−\mathrm{3}\right)}{\left({a}+\mathrm{4}\right)} \\ $$$${A}=\frac{{a}}{\mathrm{2}}×\frac{\mathrm{2}{a}\left({a}−\mathrm{3}\right)}{\left({a}+\mathrm{4}\right)}=\frac{{a}^{\mathrm{2}} \left({a}−\mathrm{3}\right)}{{a}+\mathrm{4}} \\ $$$${A}+{B}=\frac{\left(\mathrm{2}{a}−\mathrm{6}\right)\left({a}+{a}−\mathrm{7}\right)}{\mathrm{2}}=\left({a}−\mathrm{3}\right)\left(\mathrm{2}{a}−\mathrm{7}\right) \\ $$$$\frac{{A}+{B}}{{A}}=\mathrm{1}+\frac{{B}}{{A}}=\mathrm{1}+\frac{\mathrm{41}}{\mathrm{50}}=\frac{\mathrm{91}}{\mathrm{50}} \\ $$$$\frac{\left({a}−\mathrm{3}\right)\left(\mathrm{2}{a}−\mathrm{7}\right)}{\frac{{a}^{\mathrm{2}} \left({a}−\mathrm{3}\right)}{{a}+\mathrm{4}}}=\frac{\mathrm{91}}{\mathrm{50}} \\ $$$$\mathrm{9}{a}^{\mathrm{2}} +\mathrm{50}{a}−\mathrm{1400}=\mathrm{0} \\ $$$${a}=\frac{−\mathrm{50}+\sqrt{\mathrm{50}^{\mathrm{2}} +\mathrm{4}×\mathrm{9}×\mathrm{1400}}}{\mathrm{18}}=\mathrm{10} \\ $$$${SW}=\sqrt{{a}^{\mathrm{2}} +\left(\mathrm{2}{a}\right)^{\mathrm{2}} }=\mathrm{10}\sqrt{\mathrm{5}} \\ $$$$\frac{{SQ}}{{SW}}=\frac{{x}_{{Q}} }{\mathrm{2}{a}}=\frac{{a}−\mathrm{3}}{{a}+\mathrm{4}}=\frac{\mathrm{10}−\mathrm{3}}{\mathrm{10}+\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${QW}={SQ}=\frac{\mathrm{10}\sqrt{\mathrm{5}}}{\mathrm{2}}=\mathrm{5}\sqrt{\mathrm{5}} \\ $$$$\frac{{PQ}}{{PR}}=\frac{{x}_{{Q}} }{\mathrm{2}{a}−\mathrm{6}}=\frac{{a}}{{a}+\mathrm{4}}=\frac{\mathrm{10}}{\mathrm{14}}=\frac{\mathrm{5}}{\mathrm{7}} \\ $$$$\Rightarrow\frac{{QR}}{{PR}}=\frac{\mathrm{2}}{\mathrm{7}} \\ $$$$\frac{{a}}{{a}}×\frac{{x}}{{y}}×\frac{{QR}}{{RP}}=\mathrm{1} \\ $$$$\frac{{x}}{{y}}×\frac{\mathrm{2}}{\mathrm{7}}=\mathrm{1} \\ $$$$\Rightarrow\frac{{x}}{{y}}=\frac{\mathrm{7}}{\mathrm{2}} \\ $$$$\Rightarrow\frac{{x}}{{x}+{y}}=\frac{\mathrm{7}}{\mathrm{9}} \\ $$$$\Rightarrow{x}=\frac{\mathrm{7}×{QW}}{\mathrm{9}}=\frac{\mathrm{7}×\mathrm{5}\sqrt{\mathrm{5}}}{\mathrm{9}}=\frac{\mathrm{35}\sqrt{\mathrm{5}}}{\mathrm{9}}\:\checkmark \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com