Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 217447 by Tawa11 last updated on 14/Mar/25

Commented by mr W last updated on 14/Mar/25

question is wrong. the friction coefficient between cylinder and stick may not be the same as the friction coefficient between cylinder and plane. the former must be larger than the latter! i think this can be said even just by using your feeling without physics calculations.

$${question}\:{is}\:{wrong}.\:{the}\:{friction}\: \\ $$$${coefficient}\:{between}\:{cylinder}\:{and} \\ $$$${stick}\:{may}\:{not}\:{be}\:{the}\:{same}\:{as}\:{the} \\ $$$${friction}\:{coefficient}\:{between}\:{cylinder} \\ $$$${and}\:{plane}.\:{the}\:{former}\:{must}\:{be} \\ $$$${larger}\:{than}\:{the}\:{latter}!\:{i}\:{think}\:{this} \\ $$$${can}\:{be}\:{said}\:{even}\:{just}\:{by}\:{using}\:{your} \\ $$$${feeling}\:{without}\:{physics}\:{calculations}. \\ $$

Commented by Tawa11 last updated on 14/Mar/25

Thanks for your time sir. I really appreciate.

$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir}. \\ $$$$\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}. \\ $$

Commented by mr W last updated on 14/Mar/25

where did you have this question? do they have an answer?

$${where}\:{did}\:{you}\:{have}\:{this}\:{question}? \\ $$$${do}\:{they}\:{have}\:{an}\:{answer}? \\ $$

Commented by Tawa11 last updated on 14/Mar/25

Sir, I will confirm if there is answer now.

$$\mathrm{Sir},\:\mathrm{I}\:\mathrm{will}\:\mathrm{confirm}\:\mathrm{if}\:\mathrm{there}\:\mathrm{is}\:\mathrm{answer}\:\mathrm{now}. \\ $$

Commented by Tawa11 last updated on 14/Mar/25

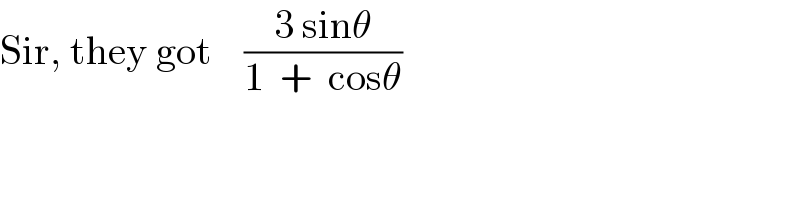
Sir, they got ((3 sinθ)/(1 + cosθ))

$$\mathrm{Sir},\:\mathrm{they}\:\mathrm{got}\:\:\:\:\frac{\mathrm{3}\:\mathrm{sin}\theta}{\mathrm{1}\:\:+\:\:\mathrm{cos}\theta} \\ $$

Commented by mr W last updated on 14/Mar/25

then the question and diagram are wrong. if the question and the diagram were right, then we had:

$${then}\:{the}\:{question}\:{and}\:{diagram}\:{are} \\ $$$${wrong}. \\ $$$${if}\:{the}\:{question}\:{and}\:{the}\:{diagram}\:{were} \\ $$$${right},\:{then}\:{we}\:{had}: \\ $$

Commented by mr W last updated on 14/Mar/25

Commented by mr W last updated on 14/Mar/25

the three forces must meet at the same point as shown. but they are not in equilibrium! (with tan φ=μ)

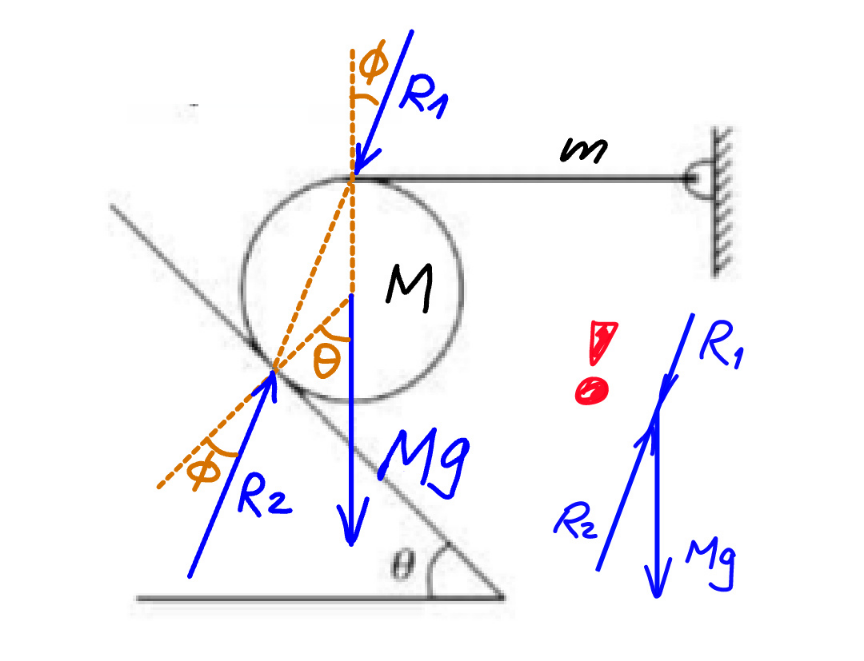
$${the}\:{three}\:{forces}\:{must}\:{meet}\:{at}\:{the} \\ $$$${same}\:{point}\:{as}\:{shown}.\:{but}\:{they}\:{are} \\ $$$${not}\:{in}\:{equilibrium}! \\ $$$$\left({with}\:\mathrm{tan}\:\phi=\mu\right) \\ $$

Commented by mr W last updated on 14/Mar/25

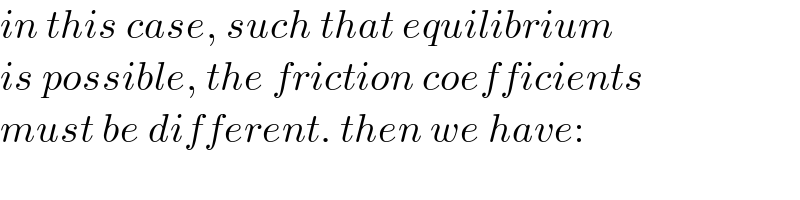
in this case, such that equilibrium is possible, the friction coefficients must be different. then we have:

$${in}\:{this}\:{case},\:{such}\:{that}\:{equilibrium}\: \\ $$$${is}\:{possible},\:{the}\:{friction}\:{coefficients} \\ $$$${must}\:{be}\:{different}.\:{then}\:{we}\:{have}: \\ $$

Commented by mr W last updated on 14/Mar/25

Commented by mr W last updated on 14/Mar/25

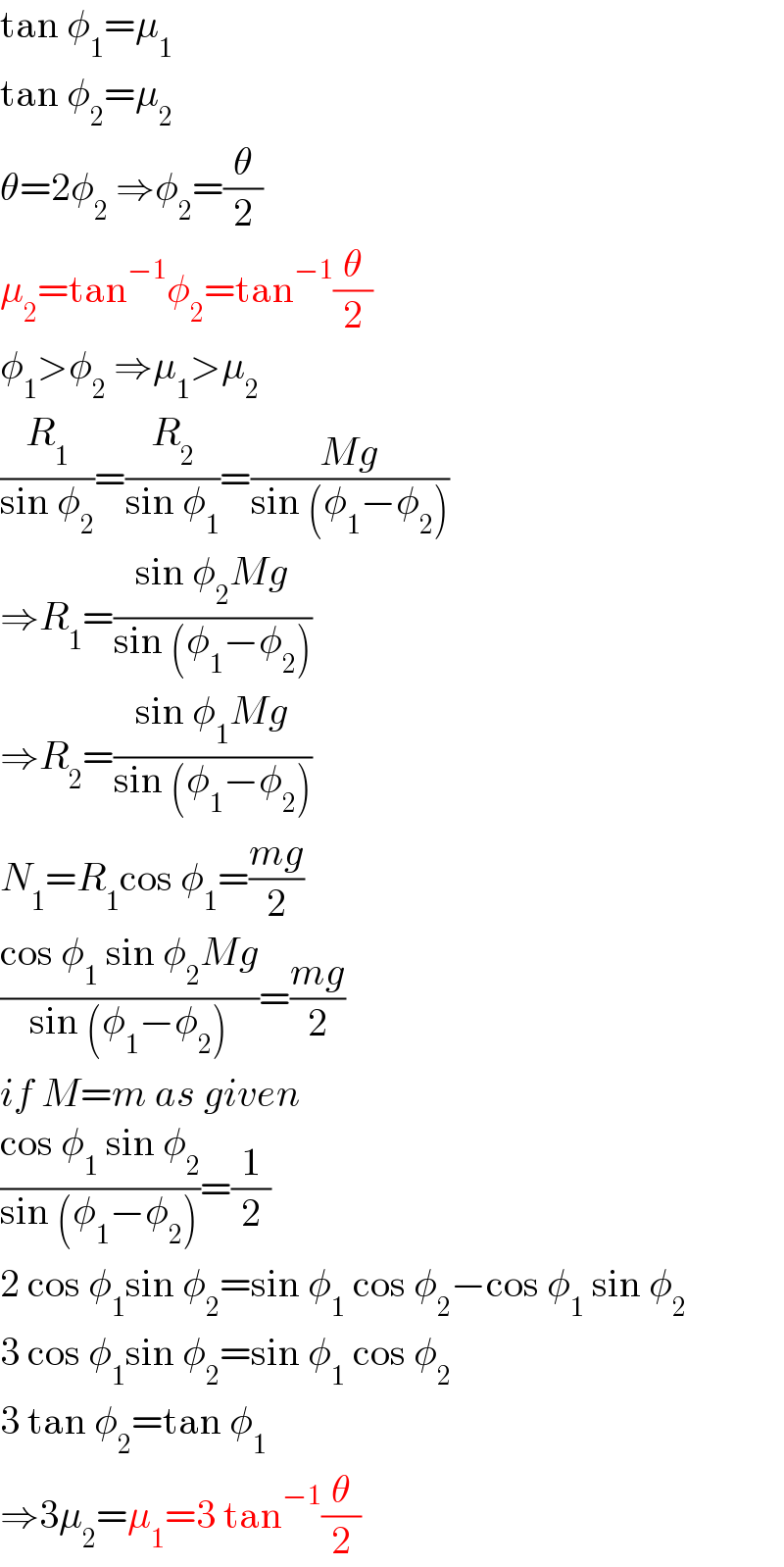
tan φ_1 =μ_1 tan φ_2 =μ_2 θ=2φ_2 ⇒φ_2 =(θ/2) μ_2 =tan^(−1) φ_2 =tan^(−1) (θ/2) φ_1 >φ_2 ⇒μ_1 >μ_2 (R_1 /(sin φ_2 ))=(R_2 /(sin φ_1 ))=((Mg)/(sin (φ_1 −φ_2 ))) ⇒R_1 =((sin φ_2 Mg)/(sin (φ_1 −φ_2 ))) ⇒R_2 =((sin φ_1 Mg)/(sin (φ_1 −φ_2 ))) N_1 =R_1 cos φ_1 =((mg)/2) ((cos φ_1 sin φ_2 Mg)/(sin (φ_1 −φ_2 )))=((mg)/2) if M=m as given ((cos φ_1 sin φ_2 )/(sin (φ_1 −φ_2 )))=(1/2) 2 cos φ_1 sin φ_2 =sin φ_1 cos φ_2 −cos φ_1 sin φ_2 3 cos φ_1 sin φ_2 =sin φ_1 cos φ_2 3 tan φ_2 =tan φ_1 ⇒3μ_2 =μ_1 =3 tan^(−1) (θ/2)

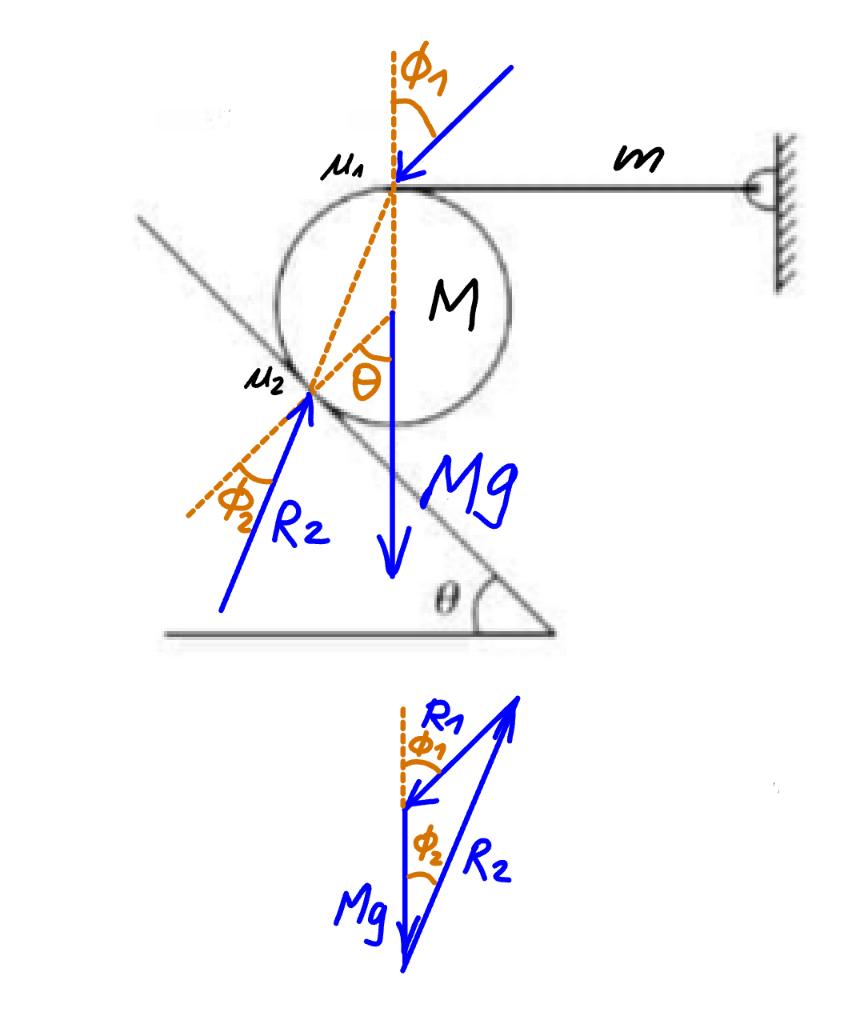
$$\mathrm{tan}\:\phi_{\mathrm{1}} =\mu_{\mathrm{1}} \\ $$$$\mathrm{tan}\:\phi_{\mathrm{2}} =\mu_{\mathrm{2}} \\ $$$$\theta=\mathrm{2}\phi_{\mathrm{2}} \:\Rightarrow\phi_{\mathrm{2}} =\frac{\theta}{\mathrm{2}} \\ $$$$\mu_{\mathrm{2}} =\mathrm{tan}^{−\mathrm{1}} \phi_{\mathrm{2}} =\mathrm{tan}^{−\mathrm{1}} \frac{\theta}{\mathrm{2}} \\ $$$$\phi_{\mathrm{1}} >\phi_{\mathrm{2}} \:\Rightarrow\mu_{\mathrm{1}} >\mu_{\mathrm{2}} \\ $$$$\frac{{R}_{\mathrm{1}} }{\mathrm{sin}\:\phi_{\mathrm{2}} }=\frac{{R}_{\mathrm{2}} }{\mathrm{sin}\:\phi_{\mathrm{1}} }=\frac{{Mg}}{\mathrm{sin}\:\left(\phi_{\mathrm{1}} −\phi_{\mathrm{2}} \right)} \\ $$$$\Rightarrow{R}_{\mathrm{1}} =\frac{\mathrm{sin}\:\phi_{\mathrm{2}} {Mg}}{\mathrm{sin}\:\left(\phi_{\mathrm{1}} −\phi_{\mathrm{2}} \right)} \\ $$$$\Rightarrow{R}_{\mathrm{2}} =\frac{\mathrm{sin}\:\phi_{\mathrm{1}} {Mg}}{\mathrm{sin}\:\left(\phi_{\mathrm{1}} −\phi_{\mathrm{2}} \right)} \\ $$$${N}_{\mathrm{1}} ={R}_{\mathrm{1}} \mathrm{cos}\:\phi_{\mathrm{1}} =\frac{{mg}}{\mathrm{2}} \\ $$$$\frac{\mathrm{cos}\:\phi_{\mathrm{1}} \:\mathrm{sin}\:\phi_{\mathrm{2}} {Mg}}{\mathrm{sin}\:\left(\phi_{\mathrm{1}} −\phi_{\mathrm{2}} \right)}=\frac{{mg}}{\mathrm{2}} \\ $$$${if}\:{M}={m}\:{as}\:{given} \\ $$$$\frac{\mathrm{cos}\:\phi_{\mathrm{1}} \:\mathrm{sin}\:\phi_{\mathrm{2}} }{\mathrm{sin}\:\left(\phi_{\mathrm{1}} −\phi_{\mathrm{2}} \right)}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{2}\:\mathrm{cos}\:\phi_{\mathrm{1}} \mathrm{sin}\:\phi_{\mathrm{2}} =\mathrm{sin}\:\phi_{\mathrm{1}} \:\mathrm{cos}\:\phi_{\mathrm{2}} −\mathrm{cos}\:\phi_{\mathrm{1}} \:\mathrm{sin}\:\phi_{\mathrm{2}} \\ $$$$\mathrm{3}\:\mathrm{cos}\:\phi_{\mathrm{1}} \mathrm{sin}\:\phi_{\mathrm{2}} =\mathrm{sin}\:\phi_{\mathrm{1}} \:\mathrm{cos}\:\phi_{\mathrm{2}} \\ $$$$\mathrm{3}\:\mathrm{tan}\:\phi_{\mathrm{2}} =\mathrm{tan}\:\phi_{\mathrm{1}} \\ $$$$\Rightarrow\mathrm{3}\mu_{\mathrm{2}} =\mu_{\mathrm{1}} =\mathrm{3}\:\mathrm{tan}^{−\mathrm{1}} \frac{\theta}{\mathrm{2}} \\ $$

Commented by mr W last updated on 15/Mar/25

what did they say as you told them that the question is wrong and therefore their answer is wrong too?

$${what}\:{did}\:{they}\:{say}\:{as}\:{you}\:{told}\:{them} \\ $$$${that}\:{the}\:{question}\:{is}\:{wrong}\:{and} \\ $$$${therefore}\:{their}\:{answer}\:{is}\:{wrong}\:{too}? \\ $$

Commented by Tawa11 last updated on 15/Mar/25

They admit the question is not well contructed sir. The lecturer said he will change it. Thanks for your time sir.

$$\mathrm{They}\:\mathrm{admit}\:\mathrm{the}\:\mathrm{question}\:\mathrm{is}\:\mathrm{not}\:\mathrm{well} \\ $$$$\mathrm{contructed}\:\mathrm{sir}. \\ $$$$\mathrm{The}\:\mathrm{lecturer}\:\mathrm{said}\:\mathrm{he}\:\mathrm{will}\:\mathrm{change}\:\mathrm{it}. \\ $$$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir}. \\ $$

Commented by mr W last updated on 15/Mar/25

so i′m right. but i wonder how they could get that answer ((3 sin θ)/(1+cos θ)) nevertheless.

$${so}\:{i}'{m}\:{right}.\:{but}\:{i}\:{wonder}\:{how}\:{they} \\ $$$${could}\:{get}\:{that}\:{answer}\:\frac{\mathrm{3}\:\mathrm{sin}\:\theta}{\mathrm{1}+\mathrm{cos}\:\theta} \\ $$$${nevertheless}. \\ $$

Answered by mr W last updated on 14/Mar/25

if the question is modified like following, then it can be solved.

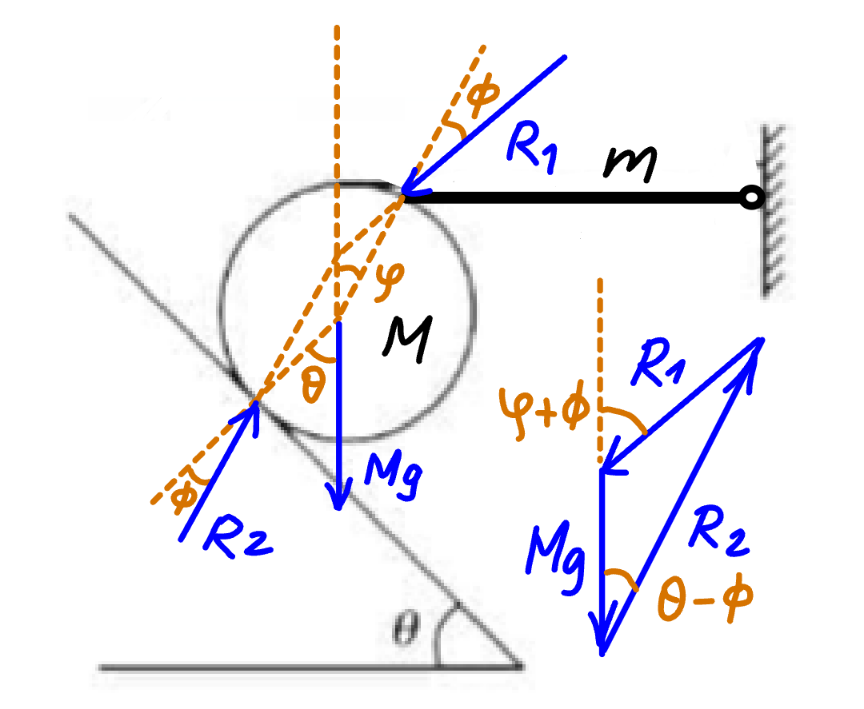
$${if}\:{the}\:{question}\:{is}\:{modified}\:{like} \\ $$$${following},\:{then}\:{it}\:{can}\:{be}\:{solved}. \\ $$

Commented by mr W last updated on 14/Mar/25

Commented by mr W last updated on 15/Mar/25

Commented by mr W last updated on 15/Mar/25

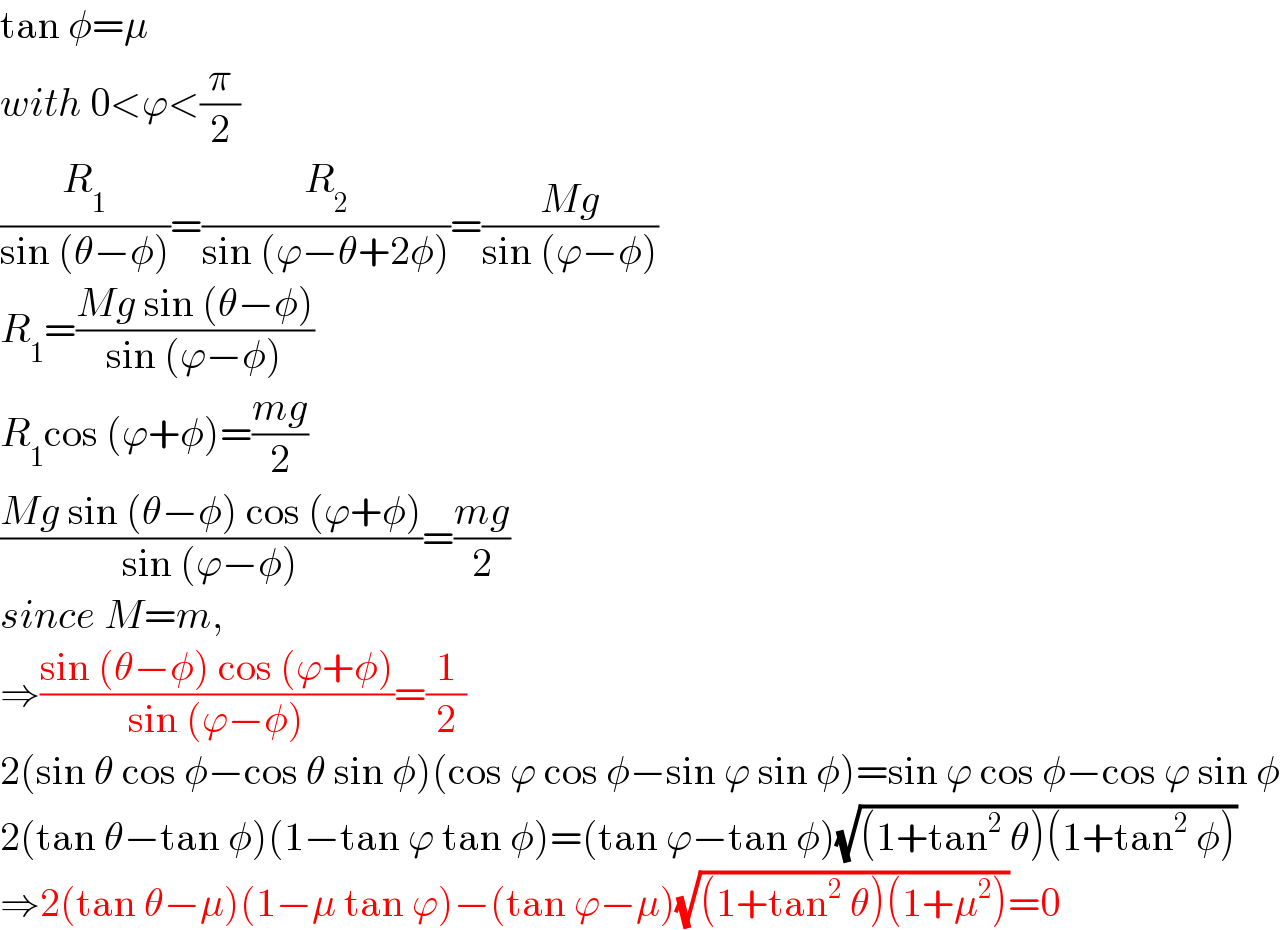
tan φ=μ with 0<ϕ<(π/2) (R_1 /(sin (θ−φ)))=(R_2 /(sin (ϕ−θ+2φ)))=((Mg)/(sin (ϕ−φ))) R_1 =((Mg sin (θ−φ))/(sin (ϕ−φ))) R_1 cos (ϕ+φ)=((mg)/2) ((Mg sin (θ−φ) cos (ϕ+φ))/(sin (ϕ−φ)))=((mg)/2) since M=m, ⇒((sin (θ−φ) cos (ϕ+φ))/(sin (ϕ−φ)))=(1/2) 2(sin θ cos φ−cos θ sin φ)(cos ϕ cos φ−sin ϕ sin φ)=sin ϕ cos φ−cos ϕ sin φ 2(tan θ−tan φ)(1−tan ϕ tan φ)=(tan ϕ−tan φ)(√((1+tan^2 θ)(1+tan^2 φ))) ⇒2(tan θ−μ)(1−μ tan ϕ)−(tan ϕ−μ)(√((1+tan^2 θ)(1+μ^2 )))=0

$$\mathrm{tan}\:\phi=\mu \\ $$$${with}\:\mathrm{0}<\varphi<\frac{\pi}{\mathrm{2}} \\ $$$$\frac{{R}_{\mathrm{1}} }{\mathrm{sin}\:\left(\theta−\phi\right)}=\frac{{R}_{\mathrm{2}} }{\mathrm{sin}\:\left(\varphi−\theta+\mathrm{2}\phi\right)}=\frac{{Mg}}{\mathrm{sin}\:\left(\varphi−\phi\right)} \\ $$$${R}_{\mathrm{1}} =\frac{{Mg}\:\mathrm{sin}\:\left(\theta−\phi\right)}{\mathrm{sin}\:\left(\varphi−\phi\right)} \\ $$$${R}_{\mathrm{1}} \mathrm{cos}\:\left(\varphi+\phi\right)=\frac{{mg}}{\mathrm{2}} \\ $$$$\frac{{Mg}\:\mathrm{sin}\:\left(\theta−\phi\right)\:\mathrm{cos}\:\left(\varphi+\phi\right)}{\mathrm{sin}\:\left(\varphi−\phi\right)}=\frac{{mg}}{\mathrm{2}} \\ $$$${since}\:{M}={m}, \\ $$$$\Rightarrow\frac{\mathrm{sin}\:\left(\theta−\phi\right)\:\mathrm{cos}\:\left(\varphi+\phi\right)}{\mathrm{sin}\:\left(\varphi−\phi\right)}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{2}\left(\mathrm{sin}\:\theta\:\mathrm{cos}\:\phi−\mathrm{cos}\:\theta\:\mathrm{sin}\:\phi\right)\left(\mathrm{cos}\:\varphi\:\mathrm{cos}\:\phi−\mathrm{sin}\:\varphi\:\mathrm{sin}\:\phi\right)=\mathrm{sin}\:\varphi\:\mathrm{cos}\:\phi−\mathrm{cos}\:\varphi\:\mathrm{sin}\:\phi \\ $$$$\mathrm{2}\left(\mathrm{tan}\:\theta−\mathrm{tan}\:\phi\right)\left(\mathrm{1}−\mathrm{tan}\:\varphi\:\mathrm{tan}\:\phi\right)=\left(\mathrm{tan}\:\varphi−\mathrm{tan}\:\phi\right)\sqrt{\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta\right)\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\phi\right)} \\ $$$$\Rightarrow\mathrm{2}\left(\mathrm{tan}\:\theta−\mu\right)\left(\mathrm{1}−\mu\:\mathrm{tan}\:\varphi\right)−\left(\mathrm{tan}\:\varphi−\mu\right)\sqrt{\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta\right)\left(\mathrm{1}+\mu^{\mathrm{2}} \right)}=\mathrm{0} \\ $$

Commented by Tawa11 last updated on 14/Mar/25

Have been waiting for something to drop here, as I saw empty space. Hahahahahaha

$$\mathrm{Have}\:\mathrm{been}\:\mathrm{waiting}\:\mathrm{for}\:\mathrm{something}\:\mathrm{to} \\ $$$$\mathrm{drop}\:\mathrm{here},\:\mathrm{as}\:\mathrm{I}\:\mathrm{saw}\:\mathrm{empty}\:\mathrm{space}. \\ $$$$\mathrm{Hahahahahaha} \\ $$

Commented by Tawa11 last updated on 14/Mar/25

Thanks sir. I really appreciate.

$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$$$\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}. \\ $$

Commented by mr W last updated on 14/Mar/25

right or not?

$${right}\:{or}\:{not}? \\ $$

Commented by Tawa11 last updated on 14/Mar/25

Right sir.

$$\mathrm{Right}\:\mathrm{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com