Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 217417 by peter frank last updated on 13/Mar/25

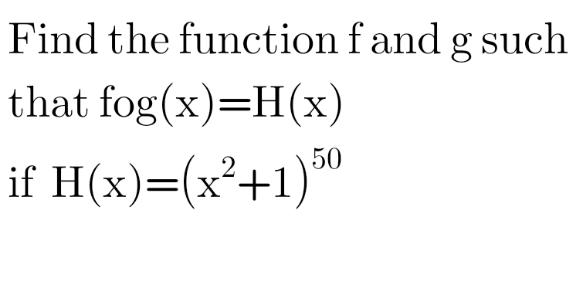
Commented by mr W last updated on 13/Mar/25

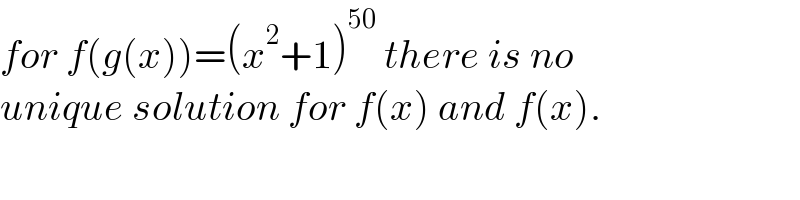
for f(g(x))=(x^2 +1)^(50) there is no unique solution for f(x) and f(x).

$${for}\:{f}\left({g}\left({x}\right)\right)=\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{50}} \:{there}\:{is}\:{no} \\ $$$${unique}\:{solution}\:{for}\:{f}\left({x}\right)\:{and}\:{f}\left({x}\right). \\ $$

Answered by SdC355 last updated on 13/Mar/25

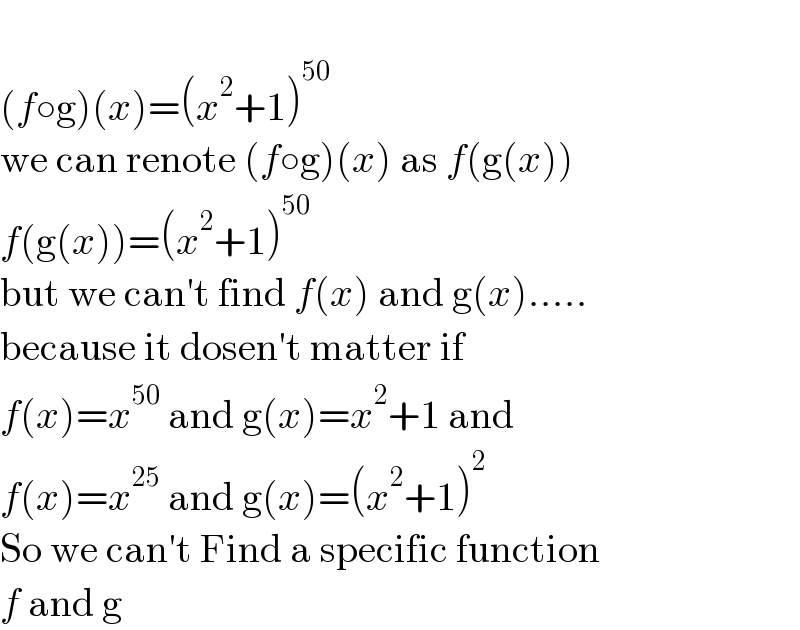
(f○g)(x)=(x^2 +1)^(50) we can renote (f○g)(x) as f(g(x)) f(g(x))=(x^2 +1)^(50) but we can′t find f(x) and g(x)..... because it dosen′t matter if f(x)=x^(50) and g(x)=x^2 +1 and f(x)=x^(25) and g(x)=(x^2 +1)^2 So we can′t Find a specific function f and g

$$\: \\ $$$$\left({f}\circ\mathrm{g}\right)\left({x}\right)=\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{50}} \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{renote}\:\left({f}\circ\mathrm{g}\right)\left({x}\right)\:\mathrm{as}\:{f}\left(\mathrm{g}\left({x}\right)\right) \\ $$$${f}\left(\mathrm{g}\left({x}\right)\right)=\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{50}} \\ $$$$\mathrm{but}\:\mathrm{we}\:\mathrm{can}'\mathrm{t}\:\mathrm{find}\:{f}\left({x}\right)\:\mathrm{and}\:\mathrm{g}\left({x}\right)..... \\ $$$$\mathrm{because}\:\mathrm{it}\:\mathrm{dosen}'\mathrm{t}\:\mathrm{matter}\:\mathrm{if} \\ $$$${f}\left({x}\right)={x}^{\mathrm{50}} \:\mathrm{and}\:\mathrm{g}\left({x}\right)={x}^{\mathrm{2}} +\mathrm{1}\:\mathrm{and} \\ $$$${f}\left({x}\right)={x}^{\mathrm{25}} \:\mathrm{and}\:\mathrm{g}\left({x}\right)=\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\mathrm{So}\:\mathrm{we}\:\mathrm{can}'\mathrm{t}\:\mathrm{Find}\:\mathrm{a}\:\mathrm{specific}\:\mathrm{function} \\ $$$${f}\:\mathrm{and}\:\mathrm{g} \\ $$

Answered by MathematicalUser2357 last updated on 13/Mar/25

f(x)=x^(50) g(x)=x^2 +1

$${f}\left({x}\right)={x}^{\mathrm{50}} \\ $$$${g}\left({x}\right)={x}^{\mathrm{2}} +\mathrm{1} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com