
Previous in Permutation and Combination Next in Permutation and Combination
Question Number 217402 by mr W last updated on 12/Mar/25

Answered by vnm last updated on 13/Mar/25

$${C}_{\mathrm{5}} ^{\mathrm{2}} \centerdot\mathrm{4}!\centerdot\mathrm{4}=\mathrm{10}\centerdot\mathrm{24}\centerdot\mathrm{4}=\mathrm{960} \\ $$
Commented by mr W last updated on 14/Mar/25

$${the}\:{boxes}\:{are}\:{identical}.\:\mathrm{4}!\:{is}\:{not} \\ $$$${needed}. \\ $$
Answered by mr W last updated on 13/Mar/25

$${C}_{\mathrm{2}} ^{\mathrm{5}} ×\mathrm{4}=\mathrm{40} \\ $$
Answered by mehdee7396 last updated on 13/Mar/25
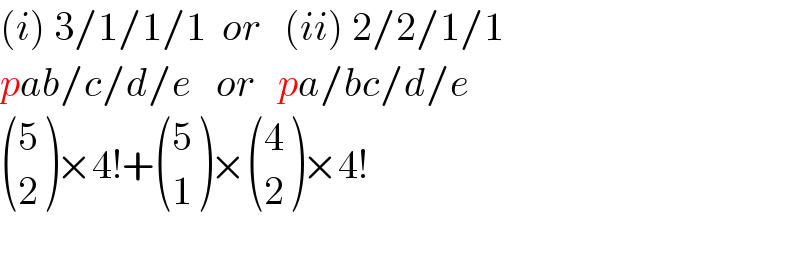
$$\left({i}\right)\:\mathrm{3}/\mathrm{1}/\mathrm{1}/\mathrm{1}\:\:{or}\:\:\:\left({ii}\right)\:\mathrm{2}/\mathrm{2}/\mathrm{1}/\mathrm{1} \\ $$$${pab}/{c}/{d}/{e}\:\:\:{or}\:\:\:{pa}/{bc}/{d}/{e} \\ $$$$\begin{pmatrix}{\mathrm{5}}\\{\mathrm{2}}\end{pmatrix}×\mathrm{4}!+\begin{pmatrix}{\mathrm{5}}\\{\mathrm{1}}\end{pmatrix}×\begin{pmatrix}{\mathrm{4}}\\{\mathrm{2}}\end{pmatrix}×\mathrm{4}! \\ $$$$ \\ $$
Commented by mr W last updated on 14/Mar/25

$${the}\:{boxes}\:{are}\:{identical}.\:\mathrm{4}!\:{is}\:{not} \\ $$$${needed}. \\ $$
Commented by mr W last updated on 13/Mar/25
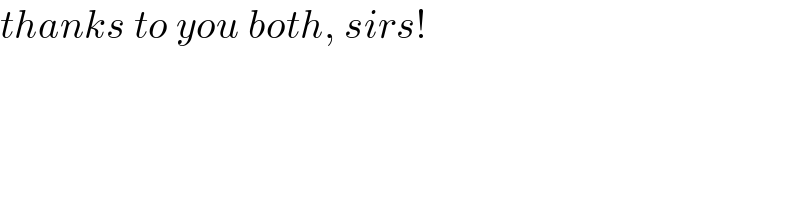
$${thanks}\:{to}\:{you}\:{both},\:{sirs}! \\ $$
Commented by mehdee7396 last updated on 14/Mar/25

$${Thank}\:{you}\:{for}\:{your}\:\:{reminder}\: \\ $$$$\:\underbrace{\lesseqgtr} \\ $$
