Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 217228 by Tawa11 last updated on 06/Mar/25

Answered by mr W last updated on 06/Mar/25

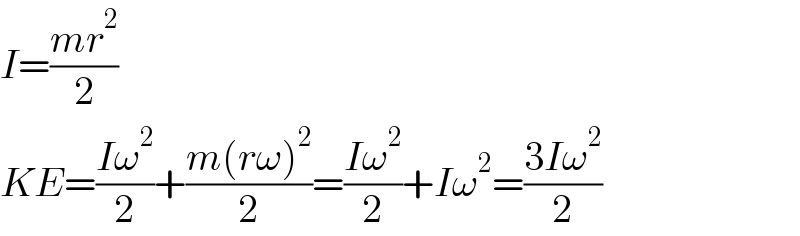
I=((mr^2 )/2) KE=((Iω^2 )/2)+((m(rω)^2 )/2)=((Iω^2 )/2)+Iω^2 =((3Iω^2 )/2)

$${I}=\frac{{mr}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${KE}=\frac{{I}\omega^{\mathrm{2}} }{\mathrm{2}}+\frac{{m}\left({r}\omega\right)^{\mathrm{2}} }{\mathrm{2}}=\frac{{I}\omega^{\mathrm{2}} }{\mathrm{2}}+{I}\omega^{\mathrm{2}} =\frac{\mathrm{3}{I}\omega^{\mathrm{2}} }{\mathrm{2}} \\ $$

Commented by Tawa11 last updated on 06/Mar/25

Thanks sir. I appreciate.

$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$

Answered by Wuji last updated on 06/Mar/25

v=ωR K_(trans) =(1/2)Mv^2 =(1/2)M(ωR)^2 K_(rot) =(1/2)Iω^2 K_(total) =K_(trans) +K_(rot) =(1/2)M(ωR)^2 +(1/2)Iω^2 K_(total) =(1/2)(Mω^2 R^2 +Iω^2 )=(1/2)ω^2 (MR^2 +I) moment of inertial about its central axis I=(1/2)MR^2 ⇒MR^2 =2I K_(total) =(1/2)ω^2 (2I+I)=(1/2)ω^2 (3I) K_(total) =(3/2)Iω^2 ✓

$$\mathrm{v}=\omega\mathrm{R} \\ $$$$\mathrm{K}_{\mathrm{trans}} =\frac{\mathrm{1}}{\mathrm{2}}\mathrm{Mv}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\mathrm{M}\left(\omega\mathrm{R}\right)^{\mathrm{2}} \\ $$$$\mathrm{K}_{\mathrm{rot}} =\frac{\mathrm{1}}{\mathrm{2}}\mathrm{I}\omega^{\mathrm{2}} \\ $$$$\mathrm{K}_{\mathrm{total}} =\mathrm{K}_{\mathrm{trans}} +\mathrm{K}_{\mathrm{rot}} \:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{M}\left(\omega\mathrm{R}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\mathrm{I}\omega^{\mathrm{2}} \\ $$$$\mathrm{K}_{\mathrm{total}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{M}\omega^{\mathrm{2}} \mathrm{R}^{\mathrm{2}} +\mathrm{I}\omega^{\mathrm{2}} \right)=\frac{\mathrm{1}}{\mathrm{2}}\omega^{\mathrm{2}} \left(\mathrm{MR}^{\mathrm{2}} +\mathrm{I}\right) \\ $$$$\mathrm{moment}\:\mathrm{of}\:\mathrm{inertial}\:\mathrm{about}\:\mathrm{its}\:\mathrm{central}\:\mathrm{axis} \\ $$$$\mathrm{I}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{MR}^{\mathrm{2}} \:\:\Rightarrow\mathrm{MR}^{\mathrm{2}} =\mathrm{2I} \\ $$$$\mathrm{K}_{\mathrm{total}} =\frac{\mathrm{1}}{\mathrm{2}}\omega^{\mathrm{2}} \left(\mathrm{2I}+\mathrm{I}\right)=\frac{\mathrm{1}}{\mathrm{2}}\omega^{\mathrm{2}} \left(\mathrm{3I}\right) \\ $$$$\mathrm{K}_{\mathrm{total}} =\frac{\mathrm{3}}{\mathrm{2}}\mathrm{I}\omega^{\mathrm{2}} \checkmark \\ $$

Commented by Tawa11 last updated on 06/Mar/25

Thanks sir. I appreciate.

$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$

Answered by MrGaster last updated on 07/Mar/25

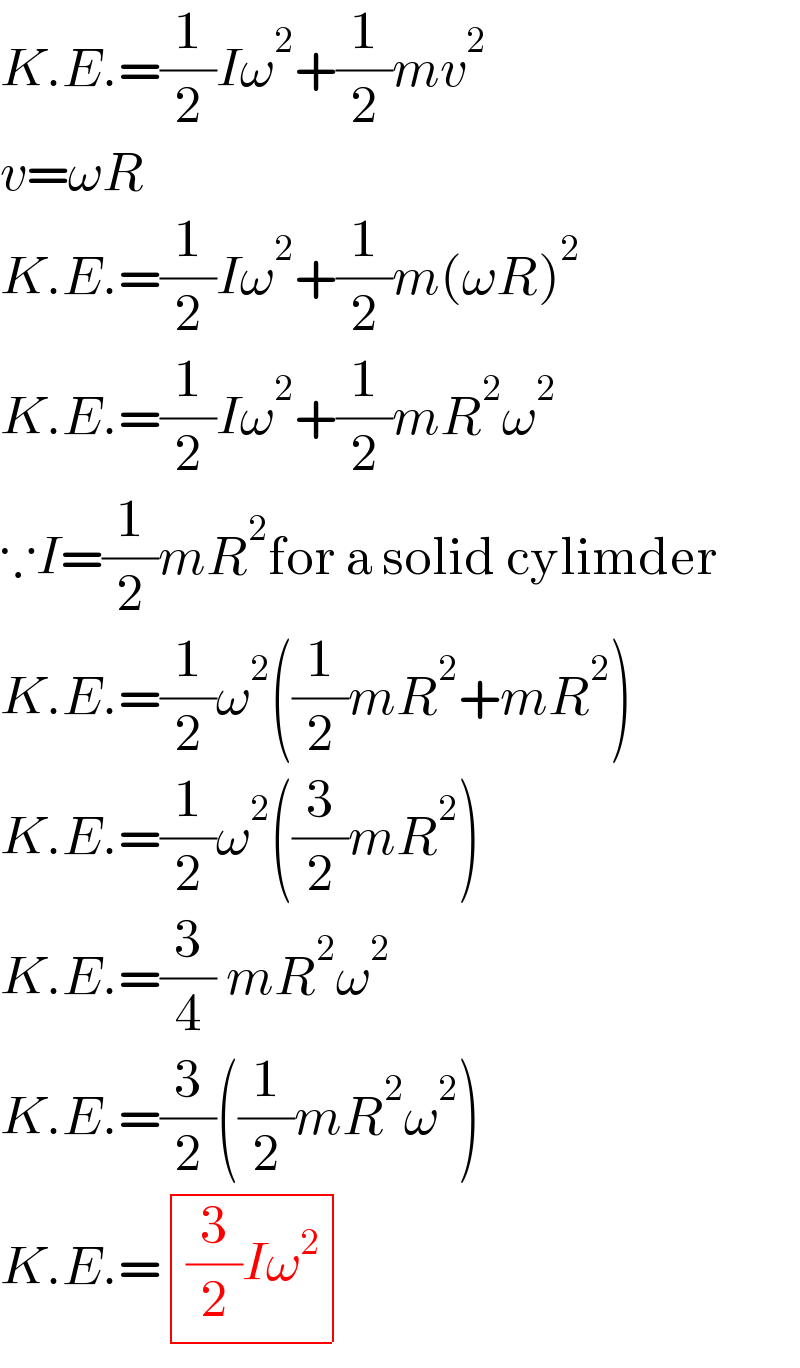
K.E.=(1/2)Iω^2 +(1/2)mv^2 v=ωR K.E.=(1/2)Iω^2 +(1/2)m(ωR)^2 K.E.=(1/2)Iω^2 +(1/2)mR^2 ω^2 ∵I=(1/2)mR^2 for a solid cylimder K.E.=(1/2)ω^2 ((1/2)mR^2 +mR^2 ) K.E.=(1/2)ω^2 ((3/2)mR^2 ) K.E.=(3/4) mR^2 ω^2 K.E.=(3/2)((1/2)mR^2 ω^2 ) K.E.= determinant ((((3/2)Iω^2 )))

$${K}.{E}.=\frac{\mathrm{1}}{\mathrm{2}}{I}\omega^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{mv}^{\mathrm{2}} \\ $$$${v}=\omega{R} \\ $$$${K}.{E}.=\frac{\mathrm{1}}{\mathrm{2}}{I}\omega^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{m}\left(\omega{R}\right)^{\mathrm{2}} \\ $$$${K}.{E}.=\frac{\mathrm{1}}{\mathrm{2}}{I}\omega^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{mR}^{\mathrm{2}} \omega^{\mathrm{2}} \\ $$$$\because{I}=\frac{\mathrm{1}}{\mathrm{2}}{mR}^{\mathrm{2}} \mathrm{for}\:\mathrm{a}\:\mathrm{solid}\:\mathrm{cylimder} \\ $$$${K}.{E}.=\frac{\mathrm{1}}{\mathrm{2}}\omega^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}{mR}^{\mathrm{2}} +{mR}^{\mathrm{2}} \right) \\ $$$${K}.{E}.=\frac{\mathrm{1}}{\mathrm{2}}\omega^{\mathrm{2}} \left(\frac{\mathrm{3}}{\mathrm{2}}{mR}^{\mathrm{2}} \right) \\ $$$${K}.{E}.=\frac{\mathrm{3}}{\mathrm{4}}\:{mR}^{\mathrm{2}} \omega^{\mathrm{2}} \\ $$$${K}.{E}.=\frac{\mathrm{3}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}{mR}^{\mathrm{2}} \omega^{\mathrm{2}} \right) \\ $$$${K}.{E}.=\begin{array}{|c|}{\frac{\mathrm{3}}{\mathrm{2}}{I}\omega^{\mathrm{2}} }\\\hline\end{array} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com