Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 217199 by cherokeesay last updated on 05/Mar/25

Commented by cherokeesay last updated on 05/Mar/25

find the value of x

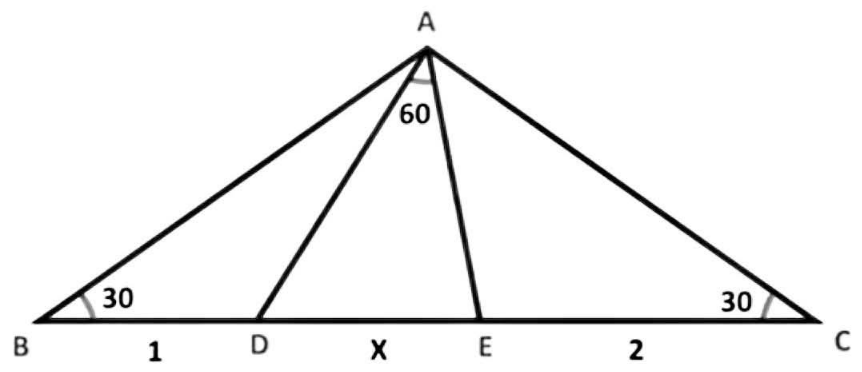
$$\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{x} \\ $$

Answered by mr W last updated on 06/Mar/25

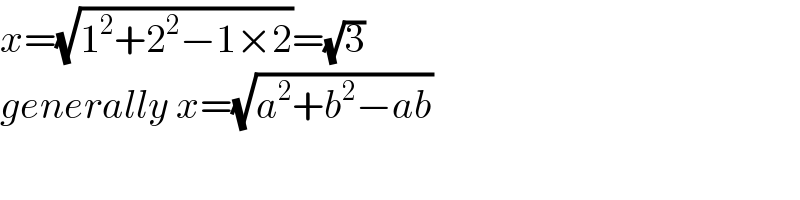
x=(√(1^2 +2^2 −1×2))=(√3) generally x=(√(a^2 +b^2 −ab))

$${x}=\sqrt{\mathrm{1}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} −\mathrm{1}×\mathrm{2}}=\sqrt{\mathrm{3}} \\ $$$${generally}\:{x}=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{ab}} \\ $$

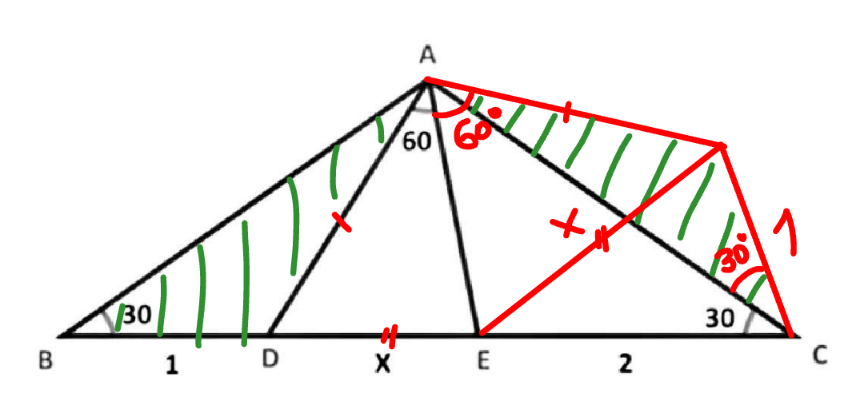
Commented by mr W last updated on 05/Mar/25

Commented by cherokeesay last updated on 05/Mar/25

thank you so much master !

$${thank}\:{you}\:{so}\:{much} \\ $$$${master}\:! \\ $$

Answered by profcedricjunior last updated on 05/Mar/25

d′apres le theoreme des sinus (c/(sin30))=((3+x)/(sin(120)))=2r=((c^2 (x+3))/(2A)) (1) (1/(sin(𝛂)))=(c/(sin𝛉))=(b/(sin30)) (2) (2/(sin(𝛃)))=(c/(sin𝛔))=(d/(sin30)) (3) or 𝛃=2𝛂 et 𝛂+𝛃=60 (x/(sin60))=(d/(sin(180−𝛉)))=(b/(sin(180−𝛔)))=(d/(sin𝛉))=(b/(sin𝛔)) (4) (3)=>c=((2sin𝛔)/(sin(𝛃))) dans (2)=>(1/(sin𝛂))=((2sin𝛔)/(sin(𝛉)sin(𝛃)))=(b/(sin30)) =>b=((2sin30×sin𝛔)/(sin(𝛉)sin(𝛃))) dans (4) (x/(sin60))=((2sin(30))/(sin(𝛉)sin(𝛃))) or 𝛃=40;𝛉=140 =>x=((2sin(30))/(sin(140)×sin(40)))

$$ \\ $$$$\boldsymbol{{d}}'\boldsymbol{{apres}}\:\boldsymbol{{le}}\:\boldsymbol{{theoreme}}\:\boldsymbol{{des}}\:\boldsymbol{{sinus}} \\ $$$$\frac{\boldsymbol{{c}}}{\boldsymbol{{sin}}\mathrm{30}}=\frac{\mathrm{3}+\boldsymbol{{x}}}{\boldsymbol{{sin}}\left(\mathrm{120}\right)}=\mathrm{2}\boldsymbol{{r}}=\frac{\boldsymbol{{c}}^{\mathrm{2}} \left(\boldsymbol{{x}}+\mathrm{3}\right)}{\mathrm{2}\boldsymbol{{A}}}\:\left(\mathrm{1}\right) \\ $$$$\frac{\mathrm{1}}{\boldsymbol{{sin}}\left(\boldsymbol{\alpha}\right)}=\frac{\boldsymbol{{c}}}{\boldsymbol{{sin}\theta}}=\frac{\boldsymbol{{b}}}{\boldsymbol{{sin}}\mathrm{30}}\:\left(\mathrm{2}\right) \\ $$$$\frac{\mathrm{2}}{\boldsymbol{{sin}}\left(\boldsymbol{\beta}\right)}=\frac{\boldsymbol{{c}}}{\boldsymbol{{sin}\sigma}}=\frac{\boldsymbol{{d}}}{\boldsymbol{{sin}}\mathrm{30}}\:\left(\mathrm{3}\right)\:\:\boldsymbol{{or}}\:\boldsymbol{\beta}=\mathrm{2}\boldsymbol{\alpha}\:\boldsymbol{{et}}\:\boldsymbol{\alpha}+\boldsymbol{\beta}=\mathrm{60} \\ $$$$\frac{\boldsymbol{{x}}}{\boldsymbol{{sin}}\mathrm{60}}=\frac{\boldsymbol{{d}}}{\boldsymbol{{sin}}\left(\mathrm{180}−\boldsymbol{\theta}\right)}=\frac{\boldsymbol{{b}}}{\boldsymbol{{sin}}\left(\mathrm{180}−\boldsymbol{\sigma}\right)}=\frac{\boldsymbol{{d}}}{\boldsymbol{{sin}\theta}}=\frac{{b}}{\boldsymbol{{sin}\sigma}}\:\left(\mathrm{4}\right) \\ $$$$\left(\mathrm{3}\right)=>\boldsymbol{{c}}=\frac{\mathrm{2}\boldsymbol{{sin}\sigma}}{\boldsymbol{{sin}}\left(\boldsymbol{\beta}\right)}\:\:\boldsymbol{{dans}}\:\left(\mathrm{2}\right)=>\frac{\mathrm{1}}{\boldsymbol{{sin}\alpha}}=\frac{\mathrm{2}\boldsymbol{{sin}\sigma}}{\boldsymbol{{sin}}\left(\boldsymbol{\theta}\right)\boldsymbol{{sin}}\left(\boldsymbol{\beta}\right)}=\frac{\boldsymbol{{b}}}{\boldsymbol{{sin}}\mathrm{30}} \\ $$$$=>\boldsymbol{{b}}=\frac{\mathrm{2}\boldsymbol{{sin}}\mathrm{30}×\boldsymbol{{sin}\sigma}}{\boldsymbol{{sin}}\left(\boldsymbol{\theta}\right)\boldsymbol{{sin}}\left(\boldsymbol{\beta}\right)}\:\:\boldsymbol{{dans}}\:\left(\mathrm{4}\right) \\ $$$$\frac{\boldsymbol{{x}}}{\boldsymbol{{sin}}\mathrm{60}}=\frac{\mathrm{2}\boldsymbol{{sin}}\left(\mathrm{30}\right)}{{s}\boldsymbol{{in}}\left(\boldsymbol{\theta}\right)\boldsymbol{{sin}}\left(\boldsymbol{\beta}\right)} \\ $$$$\boldsymbol{{or}}\:\boldsymbol{\beta}=\mathrm{40};\boldsymbol{\theta}=\mathrm{140} \\ $$$$=>\boldsymbol{{x}}=\frac{\mathrm{2}\boldsymbol{{sin}}\left(\mathrm{30}\right)}{\boldsymbol{{sin}}\left(\mathrm{140}\right)×\boldsymbol{{sin}}\left(\mathrm{40}\right)} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com