
Question Number 217198 by hardmath last updated on 05/Mar/25
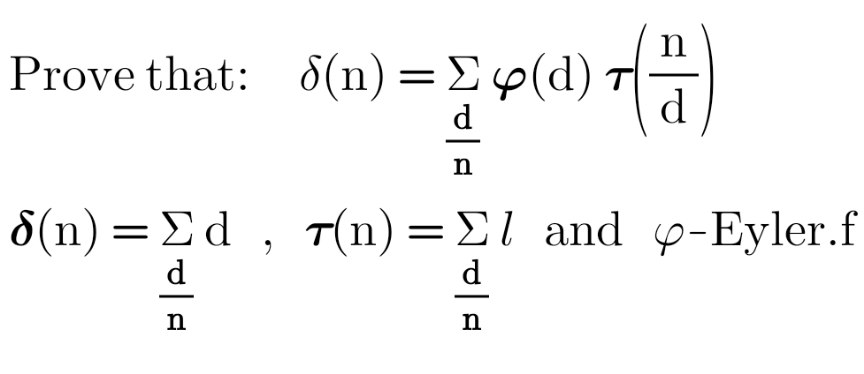
Answered by MrGaster last updated on 05/Mar/25
![δ(n)=Σ_(d∣n) d,“τ(n)=Σ_(d∣n) l⇒^((Unknown meaning)) 1” and ϕ-Euler^, s totient function δ(n)=Π_(i=1) ^k (p_i ^(a_i +1) +1)/(p_i −1) where n=Π_(i=1) ^k (a_i +1) ϕ(n)=nΠ_(i=1) ^k (1−(1/p_i )) ⇒δ(n)=Σ_(d∣n) ϕ(d)τ((n/d))=Π_(i=1) ^k (p_i ^(a_i +1) −1)/(p_i −1) [Q.E.D]](Q217201.png)
$$\delta\left({n}\right)=\underset{{d}\mid{n}} {\sum}{d},``\tau\left({n}\right)=\underset{{d}\mid{n}} {\sum}\cancel{{l}}\overset{\left(\mathrm{Unknown}\:\mathrm{meaning}\right)} {\Rightarrow}\mathrm{1}''\:\:\mathrm{and}\:\varphi-\mathrm{Euler}^{,} \mathrm{s}\:\mathrm{totient}\:\mathrm{function} \\ $$$$\delta\left({n}\right)=\underset{{i}=\mathrm{1}} {\overset{{k}} {\prod}}\left({p}_{{i}} ^{{a}_{{i}} +\mathrm{1}} +\mathrm{1}\right)/\left({p}_{{i}} −\mathrm{1}\right) \\ $$$$\mathrm{where}\:{n}=\underset{{i}=\mathrm{1}} {\overset{{k}} {\prod}}\left({a}_{{i}} +\mathrm{1}\right) \\ $$$$\varphi\left({n}\right)={n}\underset{{i}=\mathrm{1}} {\overset{{k}} {\prod}}\left(\mathrm{1}−\frac{\mathrm{1}}{{p}_{{i}} }\right) \\ $$$$\Rightarrow\delta\left({n}\right)=\underset{{d}\mid{n}} {\sum}\varphi\left({d}\right)\tau\left(\frac{{n}}{{d}}\right)=\underset{{i}=\mathrm{1}} {\overset{{k}} {\prod}}\left({p}_{{i}} ^{{a}_{{i}} +\mathrm{1}} −\mathrm{1}\right)/\left({p}_{{i}} −\mathrm{1}\right) \\ $$$$\left[{Q}.\mathrm{E}.\mathrm{D}\right] \\ $$
Commented by hardmath last updated on 16/Mar/25
$$\mathrm{thankyou}\:\mathrm{dear}\:\mathrm{professor} \\ $$
