Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 217164 by Tawa11 last updated on 03/Mar/25

Answered by issac last updated on 03/Mar/25

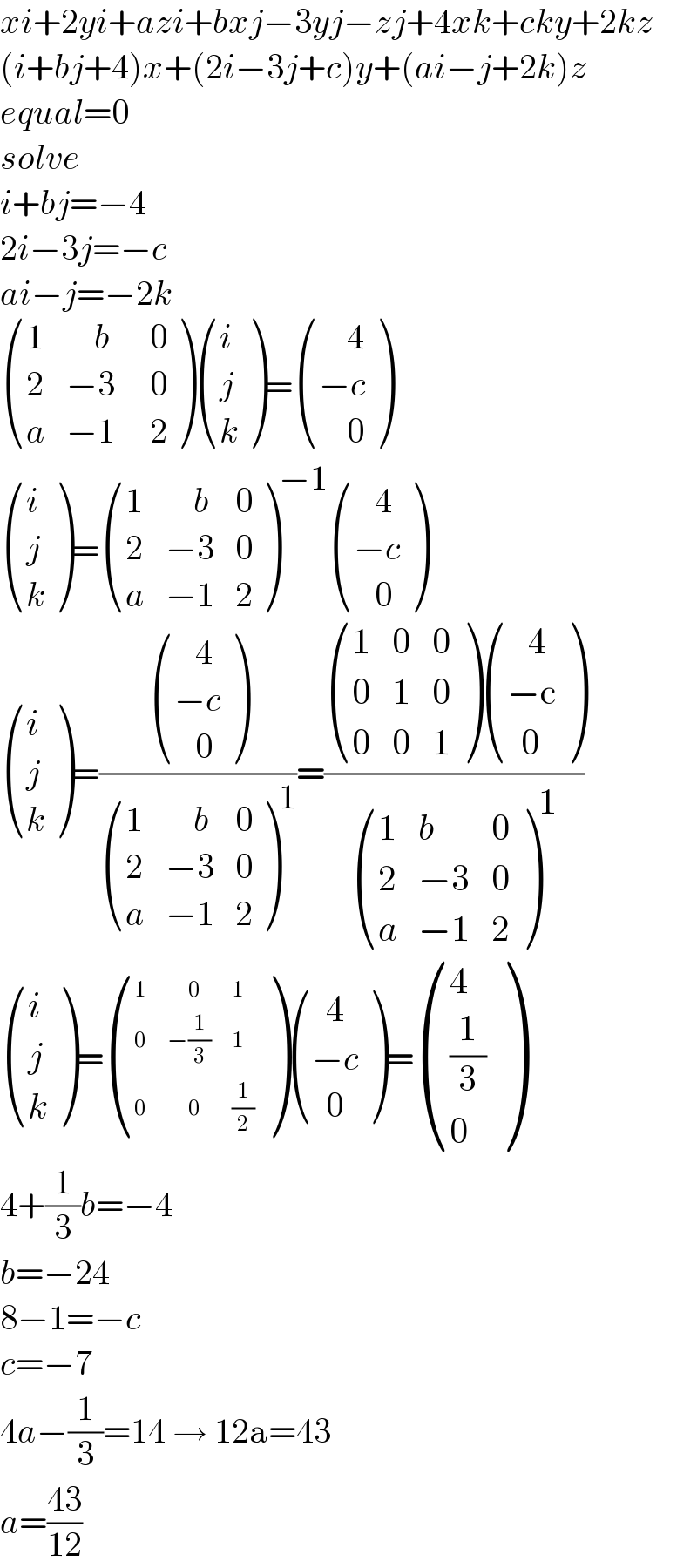
xi+2yi+azi+bxj−3yj−zj+4xk+cky+2kz (i+bj+4)x+(2i−3j+c)y+(ai−j+2k)z equal=0 solve i+bj=−4 2i−3j=−c ai−j=−2k ((1,( b),( 0)),(2,(−3),( 0)),(a,(−1),( 2)) ) ((i),(j),(k) )= ((( 4)),((−c)),(( 0)) ) ((i),(j),(k) )= ((1,( b),0),(2,(−3),0),(a,(−1),2) )^(−1) ((( 4)),((−c)),(( 0)) ) ((i),(j),(k) )=( ((( 4)),((−c)),(( 0)) )/ ((1,( b),0),(2,(−3),0),(a,(−1),2) )^1 )=(( ((1,0,0),(0,1,0),(0,0,1) ) ((( 4)),((−c)),(( 0)) ))/ ((1,b,0),(2,(−3),0),(a,(−1),2) )^1 ) ((i),(j),(k) )= ((1,( 0),1),(0,(−(1/3)),1),(0,( 0),(1/2)) ) ((( 4)),((−c)),(( 0)) )= ((4),((1/3)),(0) ) 4+(1/3)b=−4 b=−24 8−1=−c c=−7 4a−(1/3)=14 → 12a=43 a=((43)/(12))

$${xi}+\mathrm{2}{yi}+{azi}+{bxj}−\mathrm{3}{yj}−{zj}+\mathrm{4}{xk}+{cky}+\mathrm{2}{kz} \\ $$$$\left({i}+{bj}+\mathrm{4}\right){x}+\left(\mathrm{2}{i}−\mathrm{3}{j}+{c}\right){y}+\left({ai}−{j}+\mathrm{2}{k}\right){z} \\ $$$${equal}=\mathrm{0} \\ $$$${solve} \\ $$$${i}+{bj}=−\mathrm{4} \\ $$$$\mathrm{2}{i}−\mathrm{3}{j}=−{c} \\ $$$${ai}−{j}=−\mathrm{2}{k} \\ $$$$\begin{pmatrix}{\mathrm{1}}&{\:\:\:\:{b}}&{\:\:\mathrm{0}}\\{\mathrm{2}}&{−\mathrm{3}}&{\:\:\mathrm{0}}\\{{a}}&{−\mathrm{1}}&{\:\:\mathrm{2}}\end{pmatrix}\begin{pmatrix}{{i}}\\{{j}}\\{{k}}\end{pmatrix}=\begin{pmatrix}{\:\:\:\:\mathrm{4}}\\{−{c}}\\{\:\:\:\:\mathrm{0}}\end{pmatrix} \\ $$$$\begin{pmatrix}{{i}}\\{{j}}\\{{k}}\end{pmatrix}=\begin{pmatrix}{\mathrm{1}}&{\:\:\:\:{b}}&{\mathrm{0}}\\{\mathrm{2}}&{−\mathrm{3}}&{\mathrm{0}}\\{{a}}&{−\mathrm{1}}&{\mathrm{2}}\end{pmatrix}^{−\mathrm{1}} \begin{pmatrix}{\:\:\:\mathrm{4}}\\{−{c}}\\{\:\:\:\mathrm{0}}\end{pmatrix} \\ $$$$\begin{pmatrix}{{i}}\\{{j}}\\{{k}}\end{pmatrix}=\frac{\begin{pmatrix}{\:\:\:\mathrm{4}}\\{−{c}}\\{\:\:\:\mathrm{0}}\end{pmatrix}}{\begin{pmatrix}{\mathrm{1}}&{\:\:\:\:{b}}&{\mathrm{0}}\\{\mathrm{2}}&{−\mathrm{3}}&{\mathrm{0}}\\{{a}}&{−\mathrm{1}}&{\mathrm{2}}\end{pmatrix}^{\mathrm{1}} }=\frac{\begin{pmatrix}{\mathrm{1}}&{\mathrm{0}}&{\mathrm{0}}\\{\mathrm{0}}&{\mathrm{1}}&{\mathrm{0}}\\{\mathrm{0}}&{\mathrm{0}}&{\mathrm{1}}\end{pmatrix}\begin{pmatrix}{\:\:\:\mathrm{4}}\\{−\mathrm{c}}\\{\:\:\mathrm{0}}\end{pmatrix}}{\begin{pmatrix}{\mathrm{1}}&{{b}}&{\mathrm{0}}\\{\mathrm{2}}&{−\mathrm{3}}&{\mathrm{0}}\\{{a}}&{−\mathrm{1}}&{\mathrm{2}}\end{pmatrix}^{\mathrm{1}} } \\ $$$$\begin{pmatrix}{{i}}\\{{j}}\\{{k}}\end{pmatrix}=\begin{pmatrix}{\mathrm{1}}&{\:\:\:\:\:\:\mathrm{0}}&{\mathrm{1}}\\{\mathrm{0}}&{−\frac{\mathrm{1}}{\mathrm{3}}}&{\mathrm{1}}\\{\mathrm{0}}&{\:\:\:\:\:\:\mathrm{0}}&{\frac{\mathrm{1}}{\mathrm{2}}}\end{pmatrix}\begin{pmatrix}{\:\:\mathrm{4}}\\{−{c}}\\{\:\:\mathrm{0}}\end{pmatrix}=\begin{pmatrix}{\mathrm{4}}\\{\frac{\mathrm{1}}{\mathrm{3}}}\\{\mathrm{0}}\end{pmatrix} \\ $$$$\mathrm{4}+\frac{\mathrm{1}}{\mathrm{3}}{b}=−\mathrm{4} \\ $$$${b}=−\mathrm{24} \\ $$$$\mathrm{8}−\mathrm{1}=−{c} \\ $$$${c}=−\mathrm{7} \\ $$$$\mathrm{4}{a}−\frac{\mathrm{1}}{\mathrm{3}}=\mathrm{14}\:\rightarrow\:\mathrm{12a}=\mathrm{43} \\ $$$${a}=\frac{\mathrm{43}}{\mathrm{12}} \\ $$

Commented by Tawa11 last updated on 06/Mar/25

Thanks sir.

$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com