
Question Number 216925 by Engr_Jidda last updated on 24/Feb/25
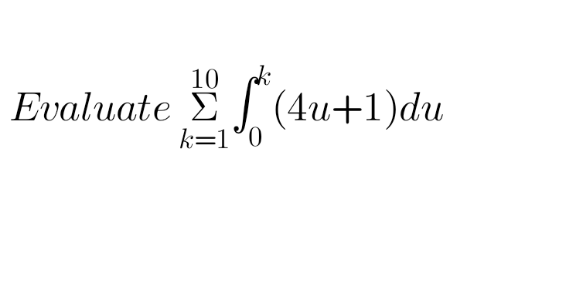
Answered by mehdee7396 last updated on 24/Feb/25
![s=∫_0 ^1 (4u+1)du+∫_0 ^2 (4u+1)du+...+∫_0 ^(10) (4u+1)du =(2u^2 +u)]_0 ^1 +(2u^2 +u)]_0 ^2 +...+(2u^2 +u)]_0 ^(10) =2(1^2 +2^2 +...+10^2 )+(1+2+...+10) =2×((10×11×21)/6)+((10×11)/2) =770+55=825](Q216927.png)
$${s}=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{4}{u}+\mathrm{1}\right){du}+\int_{\mathrm{0}} ^{\mathrm{2}} \left(\mathrm{4}{u}+\mathrm{1}\right){du}+...+\int_{\mathrm{0}} ^{\mathrm{10}} \left(\mathrm{4}{u}+\mathrm{1}\right){du} \\ $$$$\left.=\left.\left(\left.\mathrm{2}{u}^{\mathrm{2}} +{u}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} +\left(\mathrm{2}{u}^{\mathrm{2}} +{u}\right)\right]_{\mathrm{0}} ^{\mathrm{2}} +...+\left(\mathrm{2}{u}^{\mathrm{2}} +{u}\right)\right]_{\mathrm{0}} ^{\mathrm{10}} \\ $$$$=\mathrm{2}\left(\mathrm{1}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} +...+\mathrm{10}^{\mathrm{2}} \right)+\left(\mathrm{1}+\mathrm{2}+...+\mathrm{10}\right) \\ $$$$=\mathrm{2}×\frac{\mathrm{10}×\mathrm{11}×\mathrm{21}}{\mathrm{6}}+\frac{\mathrm{10}×\mathrm{11}}{\mathrm{2}} \\ $$$$=\mathrm{770}+\mathrm{55}=\mathrm{825}\: \\ $$$$ \\ $$
Commented by Engr_Jidda last updated on 25/Feb/25

$${thanks} \\ $$
Commented by Engr_Jidda last updated on 25/Feb/25

$${thanks} \\ $$
Commented by MathematicalUser2357 last updated on 26/Feb/25

$${thanks} \\ $$
