Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 216919 by Abdullahrussell last updated on 24/Feb/25

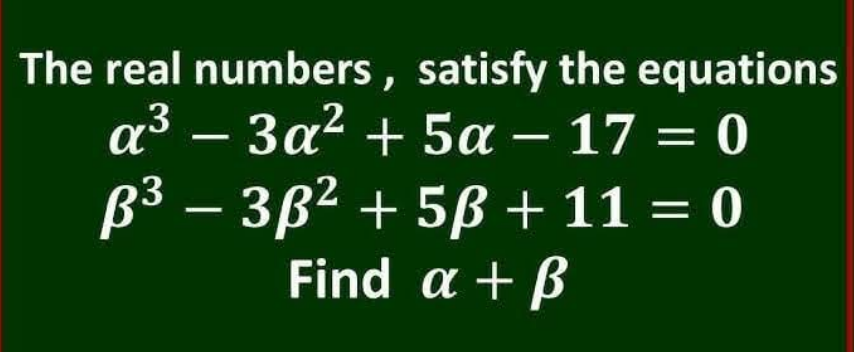
Answered by Wuji last updated on 24/Feb/25

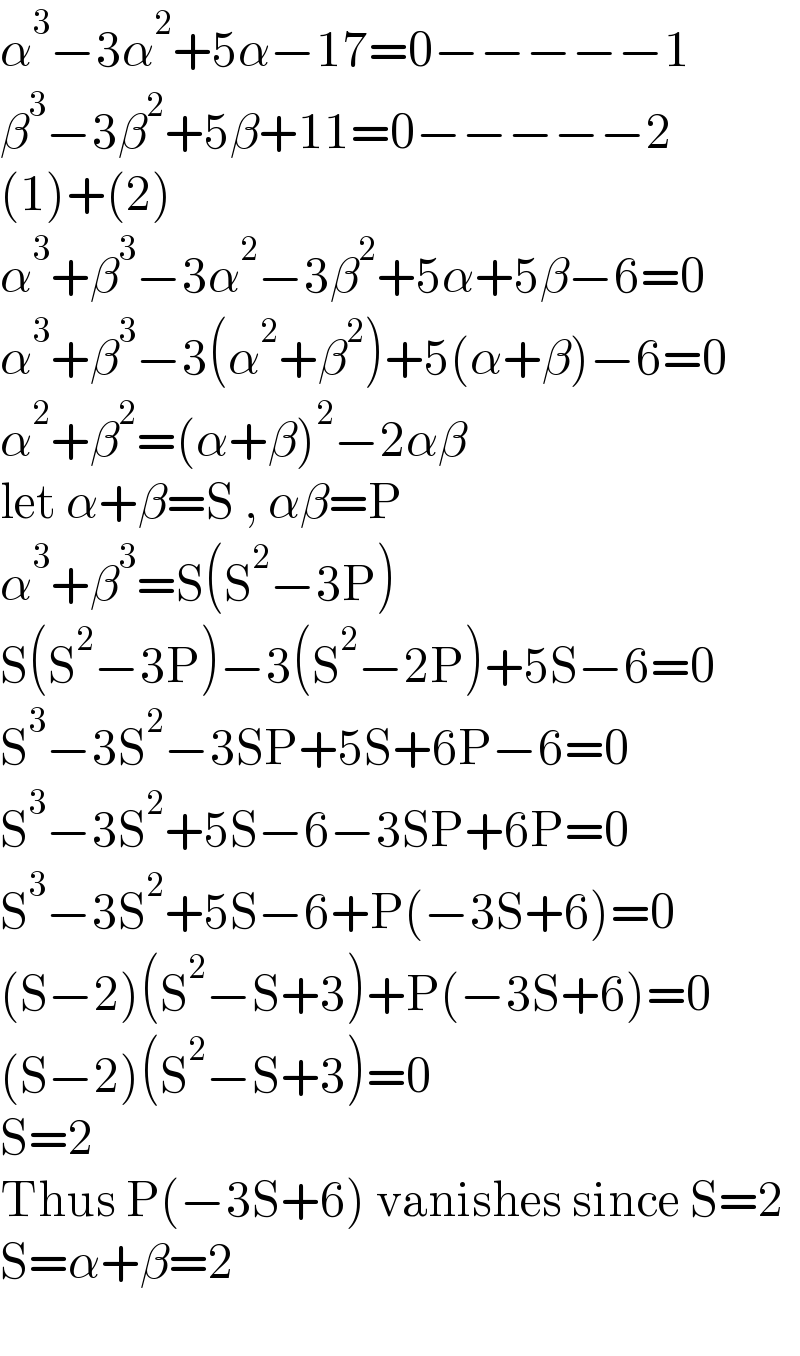
α^3 −3α^2 +5α−17=0−−−−−1 β^3 −3β^2 +5β+11=0−−−−−2 (1)+(2) α^3 +β^3 −3α^2 −3β^2 +5α+5β−6=0 α^3 +β^3 −3(α^2 +β^2 )+5(α+β)−6=0 α^2 +β^2 =(α+β)^2 −2αβ let α+β=S , αβ=P α^3 +β^3 =S(S^2 −3P) S(S^2 −3P)−3(S^2 −2P)+5S−6=0 S^3 −3S^2 −3SP+5S+6P−6=0 S^3 −3S^2 +5S−6−3SP+6P=0 S^3 −3S^2 +5S−6+P(−3S+6)=0 (S−2)(S^2 −S+3)+P(−3S+6)=0 (S−2)(S^2 −S+3)=0 S=2 Thus P(−3S+6) vanishes since S=2 S=α+β=2

$$\alpha^{\mathrm{3}} −\mathrm{3}\alpha^{\mathrm{2}} +\mathrm{5}\alpha−\mathrm{17}=\mathrm{0}−−−−−\mathrm{1} \\ $$$$\beta^{\mathrm{3}} −\mathrm{3}\beta^{\mathrm{2}} +\mathrm{5}\beta+\mathrm{11}=\mathrm{0}−−−−−\mathrm{2} \\ $$$$\left(\mathrm{1}\right)+\left(\mathrm{2}\right) \\ $$$$\alpha^{\mathrm{3}} +\beta^{\mathrm{3}} −\mathrm{3}\alpha^{\mathrm{2}} −\mathrm{3}\beta^{\mathrm{2}} +\mathrm{5}\alpha+\mathrm{5}\beta−\mathrm{6}=\mathrm{0} \\ $$$$\alpha^{\mathrm{3}} +\beta^{\mathrm{3}} −\mathrm{3}\left(\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} \right)+\mathrm{5}\left(\alpha+\beta\right)−\mathrm{6}=\mathrm{0} \\ $$$$\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} =\left(\alpha+\beta\right)^{\mathrm{2}} −\mathrm{2}\alpha\beta \\ $$$$\mathrm{let}\:\alpha+\beta=\mathrm{S}\:,\:\alpha\beta=\mathrm{P} \\ $$$$\alpha^{\mathrm{3}} +\beta^{\mathrm{3}} =\mathrm{S}\left(\mathrm{S}^{\mathrm{2}} −\mathrm{3P}\right) \\ $$$$\mathrm{S}\left(\mathrm{S}^{\mathrm{2}} −\mathrm{3P}\right)−\mathrm{3}\left(\mathrm{S}^{\mathrm{2}} −\mathrm{2P}\right)+\mathrm{5S}−\mathrm{6}=\mathrm{0} \\ $$$$\mathrm{S}^{\mathrm{3}} −\mathrm{3S}^{\mathrm{2}} −\mathrm{3SP}+\mathrm{5S}+\mathrm{6P}−\mathrm{6}=\mathrm{0} \\ $$$$\mathrm{S}^{\mathrm{3}} −\mathrm{3S}^{\mathrm{2}} +\mathrm{5S}−\mathrm{6}−\mathrm{3SP}+\mathrm{6P}=\mathrm{0} \\ $$$$\mathrm{S}^{\mathrm{3}} −\mathrm{3S}^{\mathrm{2}} +\mathrm{5S}−\mathrm{6}+\mathrm{P}\left(−\mathrm{3S}+\mathrm{6}\right)=\mathrm{0} \\ $$$$\left(\mathrm{S}−\mathrm{2}\right)\left(\mathrm{S}^{\mathrm{2}} −\mathrm{S}+\mathrm{3}\right)+\mathrm{P}\left(−\mathrm{3S}+\mathrm{6}\right)=\mathrm{0} \\ $$$$\left(\mathrm{S}−\mathrm{2}\right)\left(\mathrm{S}^{\mathrm{2}} −\mathrm{S}+\mathrm{3}\right)=\mathrm{0} \\ $$$$\mathrm{S}=\mathrm{2} \\ $$$$\mathrm{Thus}\:\mathrm{P}\left(−\mathrm{3S}+\mathrm{6}\right)\:\mathrm{vanishes}\:\mathrm{since}\:\mathrm{S}=\mathrm{2} \\ $$$$\mathrm{S}=\alpha+\beta=\mathrm{2} \\ $$$$ \\ $$

Answered by Frix last updated on 25/Feb/25

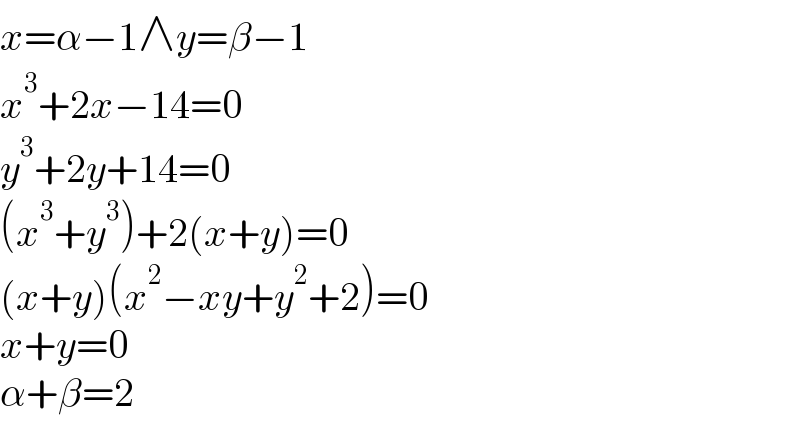
x=α−1∧y=β−1 x^3 +2x−14=0 y^3 +2y+14=0 (x^3 +y^3 )+2(x+y)=0 (x+y)(x^2 −xy+y^2 +2)=0 x+y=0 α+β=2

$${x}=\alpha−\mathrm{1}\wedge{y}=\beta−\mathrm{1} \\ $$$${x}^{\mathrm{3}} +\mathrm{2}{x}−\mathrm{14}=\mathrm{0} \\ $$$${y}^{\mathrm{3}} +\mathrm{2}{y}+\mathrm{14}=\mathrm{0} \\ $$$$\left({x}^{\mathrm{3}} +{y}^{\mathrm{3}} \right)+\mathrm{2}\left({x}+{y}\right)=\mathrm{0} \\ $$$$\left({x}+{y}\right)\left({x}^{\mathrm{2}} −{xy}+{y}^{\mathrm{2}} +\mathrm{2}\right)=\mathrm{0} \\ $$$${x}+{y}=\mathrm{0} \\ $$$$\alpha+\beta=\mathrm{2} \\ $$

Commented by Abdullahrussell last updated on 25/Feb/25

Sir, great solutions. Thanks.

$$\:\:{Sir},\:{great}\:{solutions}.\:{Thanks}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com