
Question Number 216855 by BaliramKumar last updated on 23/Feb/25
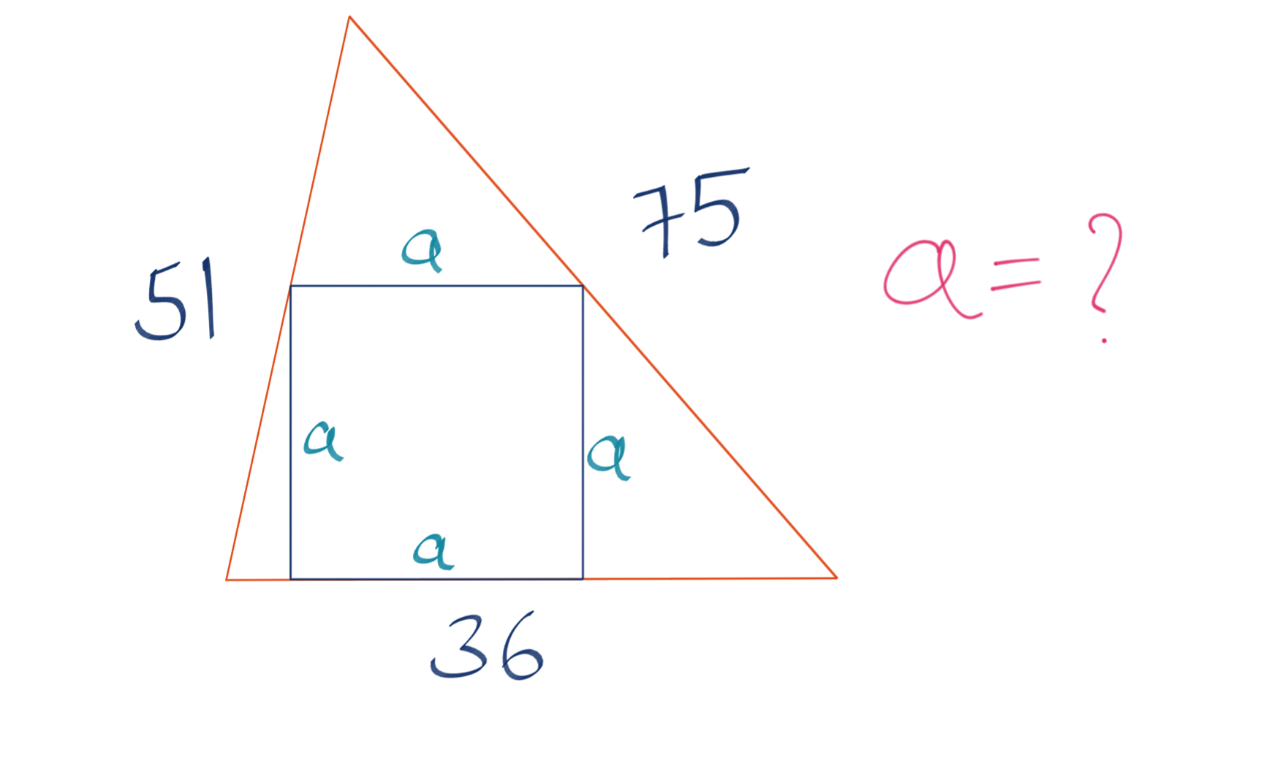
Answered by AntonCWX08 last updated on 23/Feb/25
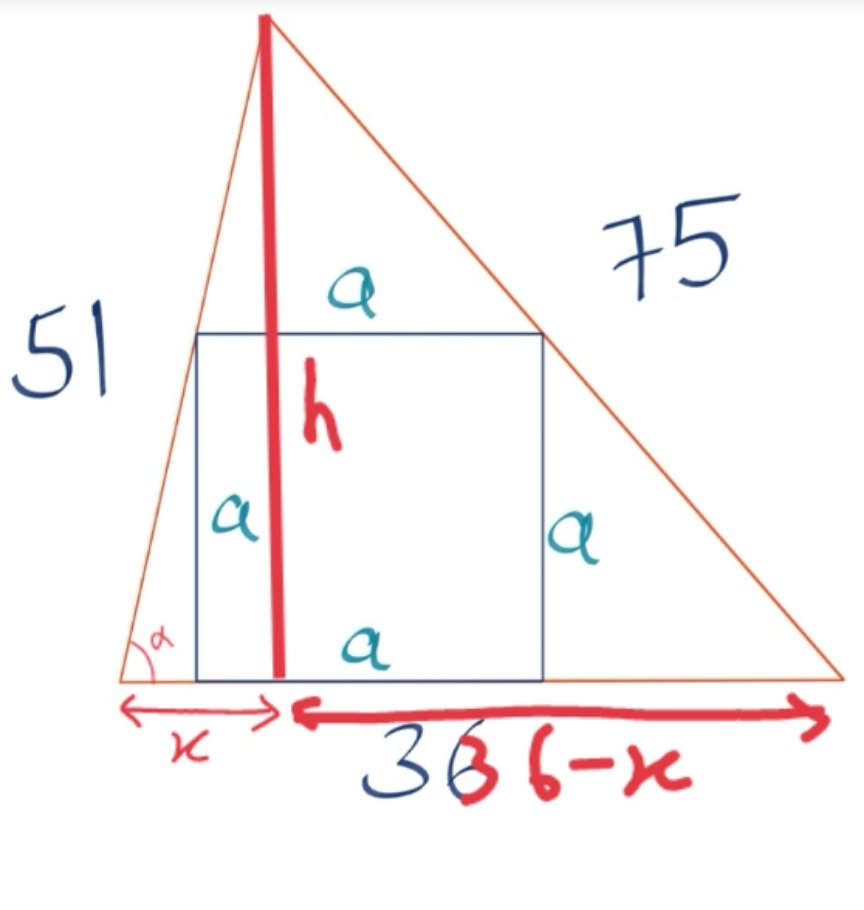
Commented by AntonCWX08 last updated on 23/Feb/25
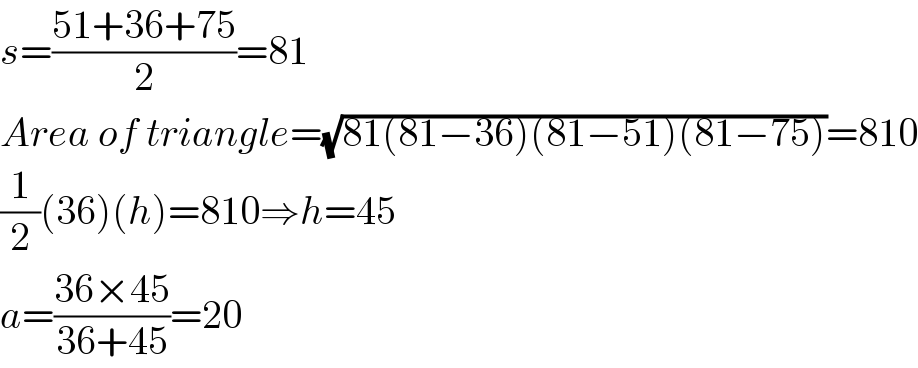
$${s}=\frac{\mathrm{51}+\mathrm{36}+\mathrm{75}}{\mathrm{2}}=\mathrm{81} \\ $$$${Area}\:{of}\:{triangle}=\sqrt{\mathrm{81}\left(\mathrm{81}−\mathrm{36}\right)\left(\mathrm{81}−\mathrm{51}\right)\left(\mathrm{81}−\mathrm{75}\right)}=\mathrm{810} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{36}\right)\left({h}\right)=\mathrm{810}\Rightarrow{h}=\mathrm{45} \\ $$$${a}=\frac{\mathrm{36}×\mathrm{45}}{\mathrm{36}+\mathrm{45}}=\mathrm{20} \\ $$
Commented by AntonCWX08 last updated on 23/Feb/25
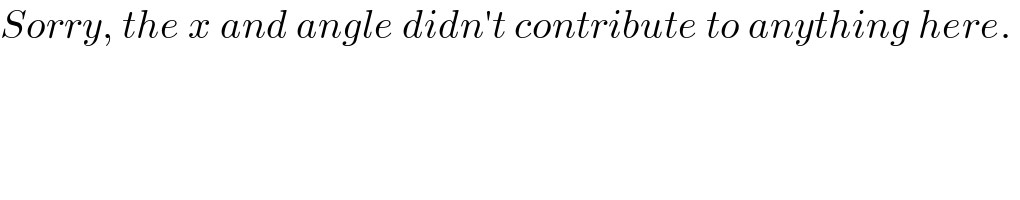
$${Sorry},\:{the}\:{x}\:{and}\:{angle}\:{didn}'{t}\:{contribute}\:{to}\:{anything}\:{here}.\: \\ $$
Commented by Ari last updated on 25/Feb/25

$${why}\:{a}=\frac{\mathrm{36}×\mathrm{45}}{\mathrm{36}+\mathrm{45}}\:???????? \\ $$
Answered by mehdee7396 last updated on 26/Feb/25
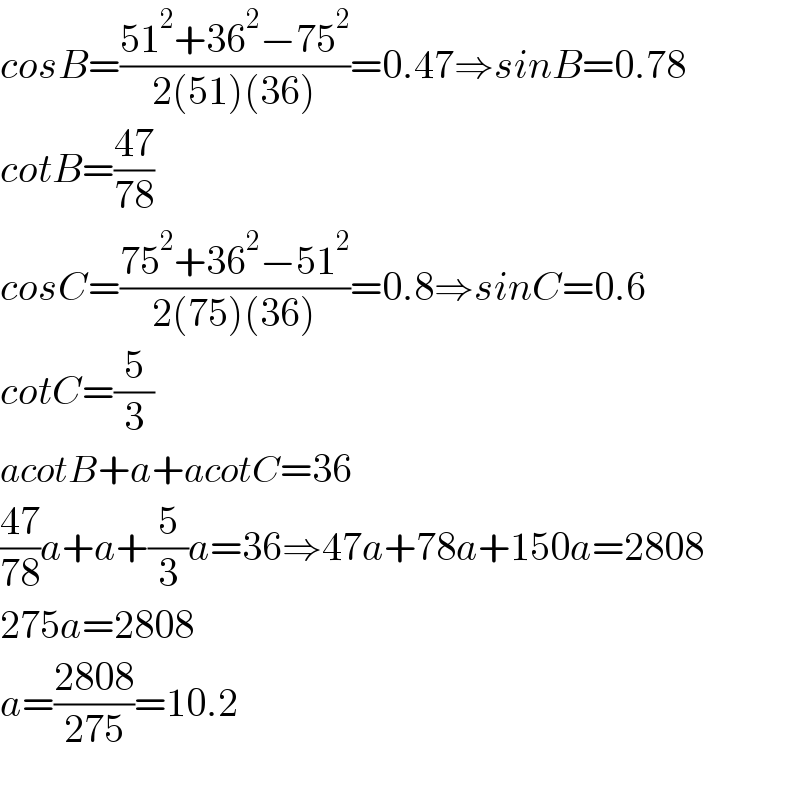
$${cosB}=\frac{\mathrm{51}^{\mathrm{2}} +\mathrm{36}^{\mathrm{2}} −\mathrm{75}^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{51}\right)\left(\mathrm{36}\right)}=\mathrm{0}.\mathrm{47}\Rightarrow{sinB}=\mathrm{0}.\mathrm{78} \\ $$$${cotB}=\frac{\mathrm{47}}{\mathrm{78}} \\ $$$${cosC}=\frac{\mathrm{75}^{\mathrm{2}} +\mathrm{36}^{\mathrm{2}} −\mathrm{51}^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{75}\right)\left(\mathrm{36}\right)}=\mathrm{0}.\mathrm{8}\Rightarrow{sinC}=\mathrm{0}.\mathrm{6} \\ $$$${cotC}=\frac{\mathrm{5}}{\mathrm{3}} \\ $$$${acotB}+{a}+{acotC}=\mathrm{36} \\ $$$$\frac{\mathrm{47}}{\mathrm{78}}{a}+{a}+\frac{\mathrm{5}}{\mathrm{3}}{a}=\mathrm{36}\Rightarrow\mathrm{47}{a}+\mathrm{78}{a}+\mathrm{150}{a}=\mathrm{2808} \\ $$$$\mathrm{275}{a}=\mathrm{2808} \\ $$$${a}=\frac{\mathrm{2808}}{\mathrm{275}}=\mathrm{10}.\mathrm{2} \\ $$$$ \\ $$
