Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 216827 by Tawa11 last updated on 22/Feb/25

Commented by Tawa11 last updated on 22/Feb/25

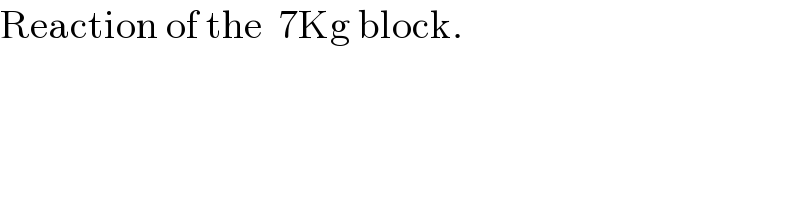
Reaction of the 7Kg block.

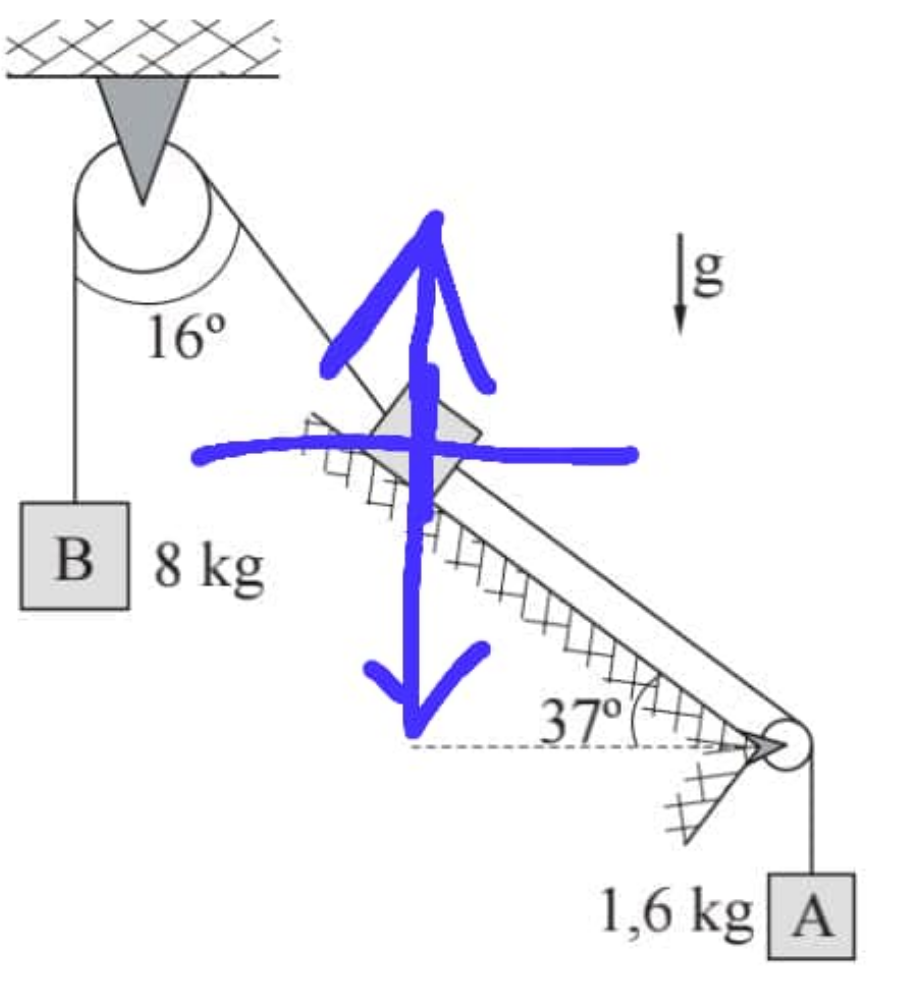
$$\mathrm{Reaction}\:\mathrm{of}\:\mathrm{the}\:\:\mathrm{7Kg}\:\mathrm{block}. \\ $$

Answered by mr W last updated on 22/Feb/25

Commented by mr W last updated on 23/Feb/25

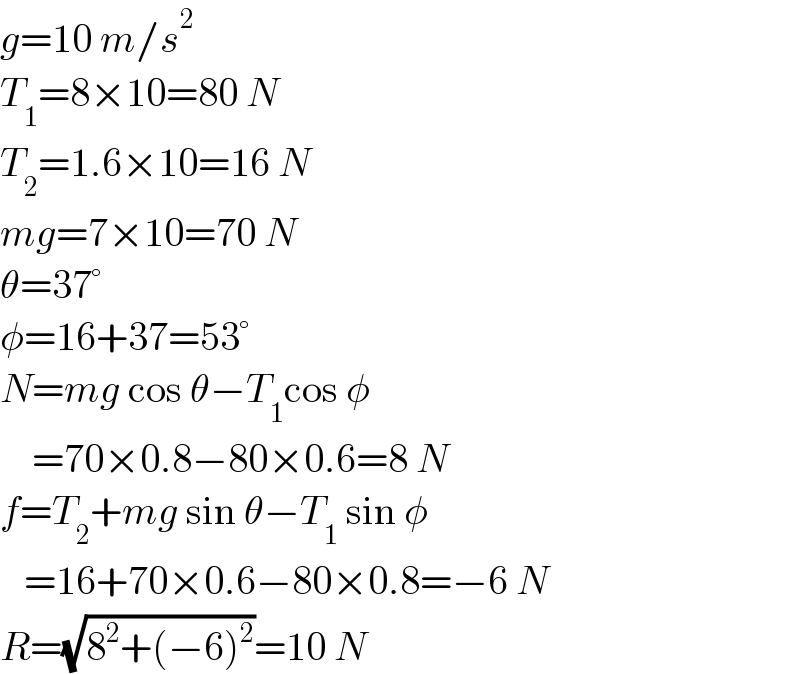
g=10 m/s^2 T_1 =8×10=80 N T_2 =1.6×10=16 N mg=7×10=70 N θ=37° φ=16+37=53° N=mg cos θ−T_1 cos φ =70×0.8−80×0.6=8 N f=T_2 +mg sin θ−T_1 sin φ =16+70×0.6−80×0.8=−6 N R=(√(8^2 +(−6)^2 ))=10 N

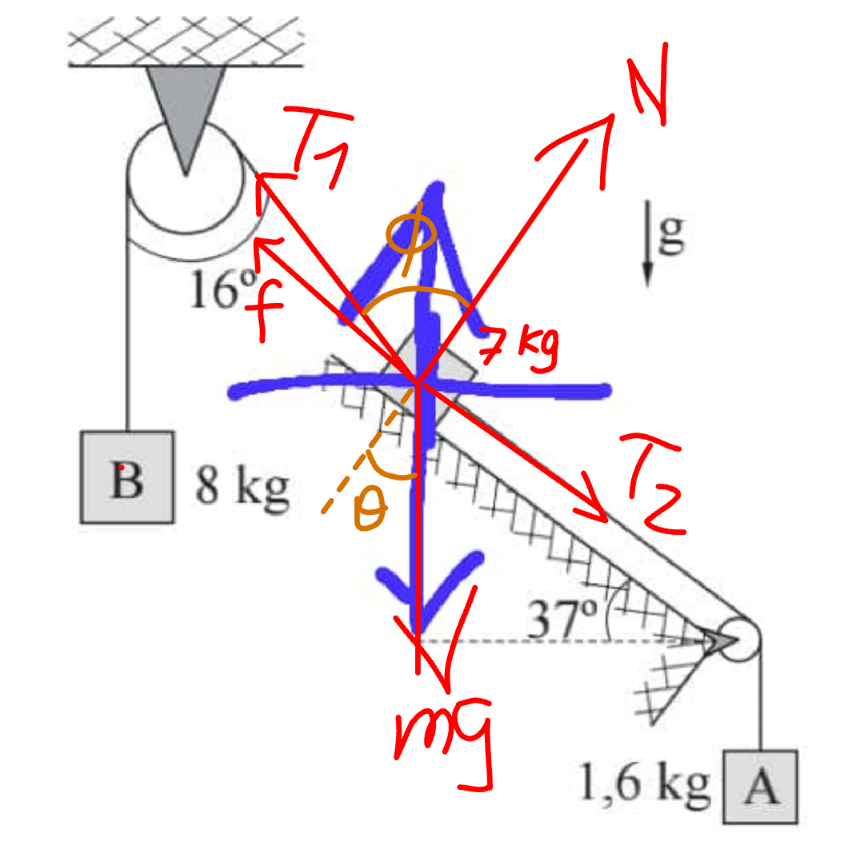
$${g}=\mathrm{10}\:{m}/{s}^{\mathrm{2}} \\ $$$${T}_{\mathrm{1}} =\mathrm{8}×\mathrm{10}=\mathrm{80}\:{N} \\ $$$${T}_{\mathrm{2}} =\mathrm{1}.\mathrm{6}×\mathrm{10}=\mathrm{16}\:{N} \\ $$$${mg}=\mathrm{7}×\mathrm{10}=\mathrm{70}\:{N} \\ $$$$\theta=\mathrm{37}° \\ $$$$\phi=\mathrm{16}+\mathrm{37}=\mathrm{53}° \\ $$$${N}={mg}\:\mathrm{cos}\:\theta−{T}_{\mathrm{1}} \mathrm{cos}\:\phi \\ $$$$\:\:\:\:=\mathrm{70}×\mathrm{0}.\mathrm{8}−\mathrm{80}×\mathrm{0}.\mathrm{6}=\mathrm{8}\:{N} \\ $$$${f}={T}_{\mathrm{2}} +{mg}\:\mathrm{sin}\:\theta−{T}_{\mathrm{1}} \:\mathrm{sin}\:\phi \\ $$$$\:\:\:=\mathrm{16}+\mathrm{70}×\mathrm{0}.\mathrm{6}−\mathrm{80}×\mathrm{0}.\mathrm{8}=−\mathrm{6}\:{N} \\ $$$${R}=\sqrt{\mathrm{8}^{\mathrm{2}} +\left(−\mathrm{6}\right)^{\mathrm{2}} }=\mathrm{10}\:{N} \\ $$

Commented by Tawa11 last updated on 22/Feb/25

Thanks for your time sir. I appreciate sir.

$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir}. \\ $$$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{sir}. \\ $$

Commented by mr W last updated on 22/Feb/25

right or wrong?

$${right}\:{or}\:{wrong}? \\ $$

Commented by Tawa11 last updated on 22/Feb/25

I will get back sir. I don′t know the answer for now. Thanks sir.

$$\mathrm{I}\:\mathrm{will}\:\mathrm{get}\:\mathrm{back}\:\mathrm{sir}. \\ $$$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{know}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{for}\:\mathrm{now}. \\ $$$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$

Commented by mr W last updated on 23/Feb/25

basically i know that my answer is right. what i meant is what do you think if it is right, in other words if you can follow and use it.

$${basically}\:{i}\:{know}\:{that}\:{my}\:{answer}\:{is} \\ $$$${right}.\:{what}\:{i}\:{meant}\:{is}\:{what}\:{do}\:{you} \\ $$$${think}\:{if}\:{it}\:{is}\:{right},\:{in}\:{other}\:{words}\: \\ $$$${if}\:{you}\:{can}\:{follow}\:{and}\:{use}\:{it}. \\ $$

Commented by Tawa11 last updated on 23/Feb/25

What he showed me is saying 9.8 sir

$$\mathrm{What}\:\mathrm{he}\:\mathrm{showed}\:\mathrm{me}\:\mathrm{is}\:\mathrm{saying}\:\mathrm{9}.\mathrm{8}\:\mathrm{sir} \\ $$

Commented by Tawa11 last updated on 23/Feb/25

Commented by Tawa11 last updated on 23/Feb/25

Is this correct sir?

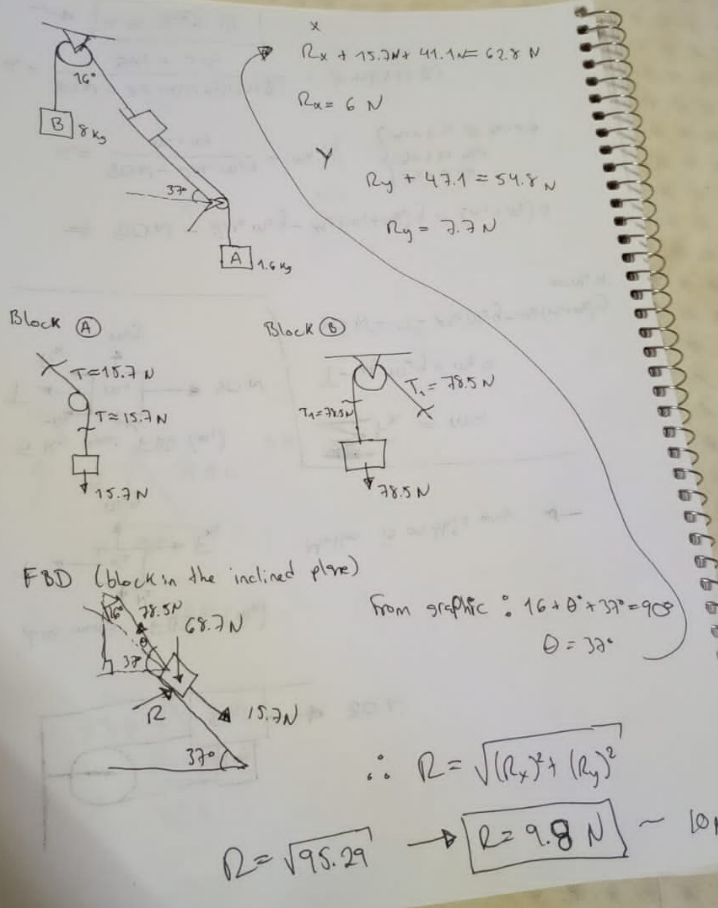
$$\mathrm{Is}\:\mathrm{this}\:\mathrm{correct}\:\mathrm{sir}? \\ $$

Commented by mr W last updated on 23/Feb/25

i just calculated N. similarly we can calculate f. then we can calculate the resultant R. if his result is right, you should be able to judge if you have followed my solution.

$${i}\:{just}\:{calculated}\:{N}.\:{similarly}\:{we}\: \\ $$$${can}\:{calculate}\:{f}.\:{then}\:{we}\:{can}\: \\ $$$${calculate}\:{the}\:{resultant}\:{R}. \\ $$$${if}\:{his}\:{result}\:{is}\:{right},\:{you}\:{should}\:{be}\: \\ $$$${able}\:{to}\:{judge}\:{if}\:{you}\:{have}\:{followed}\:{my} \\ $$$${solution}. \\ $$

Commented by Tawa11 last updated on 25/Feb/25

Yes sir.

$$\mathrm{Yes}\:\mathrm{sir}. \\ $$

Commented by Tawa11 last updated on 25/Feb/25

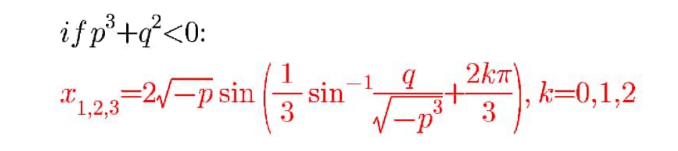
Commented by Tawa11 last updated on 25/Feb/25

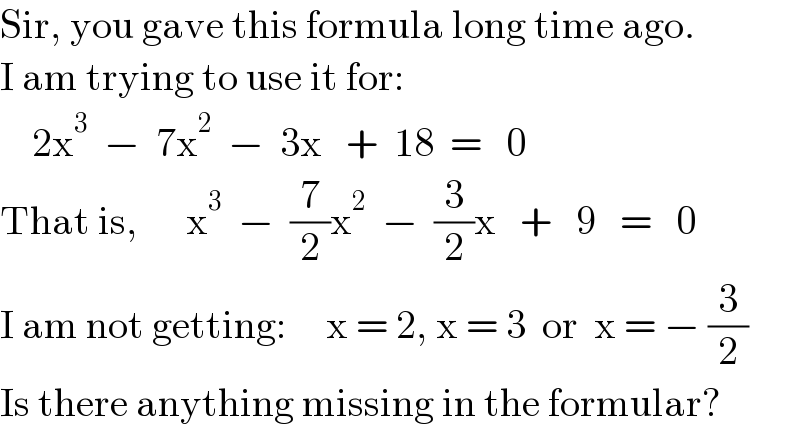
Sir, you gave this formula long time ago. I am trying to use it for: 2x^3 − 7x^2 − 3x + 18 = 0 That is, x^3 − (7/2)x^2 − (3/2)x + 9 = 0 I am not getting: x = 2, x = 3 or x = − (3/2) Is there anything missing in the formular?

$$\mathrm{Sir},\:\mathrm{you}\:\mathrm{gave}\:\mathrm{this}\:\mathrm{formula}\:\mathrm{long}\:\mathrm{time}\:\mathrm{ago}. \\ $$$$\mathrm{I}\:\mathrm{am}\:\mathrm{trying}\:\mathrm{to}\:\mathrm{use}\:\mathrm{it}\:\mathrm{for}: \\ $$$$\:\:\:\:\mathrm{2x}^{\mathrm{3}} \:\:−\:\:\mathrm{7x}^{\mathrm{2}} \:\:−\:\:\mathrm{3x}\:\:\:+\:\:\mathrm{18}\:\:=\:\:\:\mathrm{0} \\ $$$$\mathrm{That}\:\mathrm{is},\:\:\:\:\:\:\mathrm{x}^{\mathrm{3}} \:\:−\:\:\frac{\mathrm{7}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} \:\:−\:\:\frac{\mathrm{3}}{\mathrm{2}}\mathrm{x}\:\:\:+\:\:\:\mathrm{9}\:\:\:=\:\:\:\mathrm{0} \\ $$$$\mathrm{I}\:\mathrm{am}\:\mathrm{not}\:\mathrm{getting}:\:\:\:\:\:\mathrm{x}\:=\:\mathrm{2},\:\mathrm{x}\:=\:\mathrm{3}\:\:\mathrm{or}\:\:\mathrm{x}\:=\:−\:\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\mathrm{Is}\:\mathrm{there}\:\mathrm{anything}\:\mathrm{missing}\:\mathrm{in}\:\mathrm{the}\:\mathrm{formular}? \\ $$

Commented by mr W last updated on 26/Feb/25

no!

$${no}! \\ $$

Commented by Tawa11 last updated on 26/Feb/25

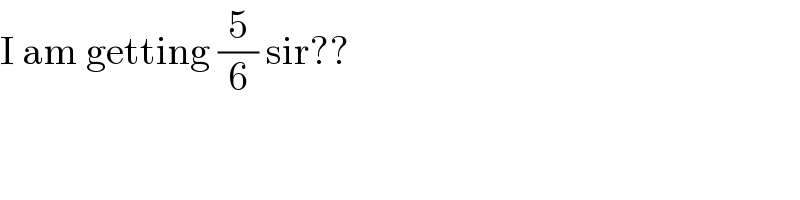
I am getting (5/6) sir??

$$\mathrm{I}\:\mathrm{am}\:\mathrm{getting}\:\frac{\mathrm{5}}{\mathrm{6}}\:\mathrm{sir}?? \\ $$

Commented by Tawa11 last updated on 26/Feb/25

x = 2(√((67)/(36))) sin[(1/3)sin^(− 1) ((((55)/(27))/( (√((((67)/(36)))^3 ))))) + 0] = (5/6) p = − ((67)/(36)) and q = ((55)/(27))

$$\:\:\:\mathrm{x}\:\:=\:\:\mathrm{2}\sqrt{\frac{\mathrm{67}}{\mathrm{36}}}\:\mathrm{sin}\left[\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\:\mathrm{1}} \left(\frac{\frac{\mathrm{55}}{\mathrm{27}}}{\:\sqrt{\left(\frac{\mathrm{67}}{\mathrm{36}}\right)^{\mathrm{3}} }}\right)\:+\:\mathrm{0}\right]\:\:=\:\:\frac{\mathrm{5}}{\mathrm{6}} \\ $$$$\mathrm{p}\:\:=\:\:−\:\frac{\mathrm{67}}{\mathrm{36}}\:\:\:\mathrm{and}\:\:\:\mathrm{q}\:\:=\:\:\frac{\mathrm{55}}{\mathrm{27}} \\ $$

Commented by mr W last updated on 26/Feb/25

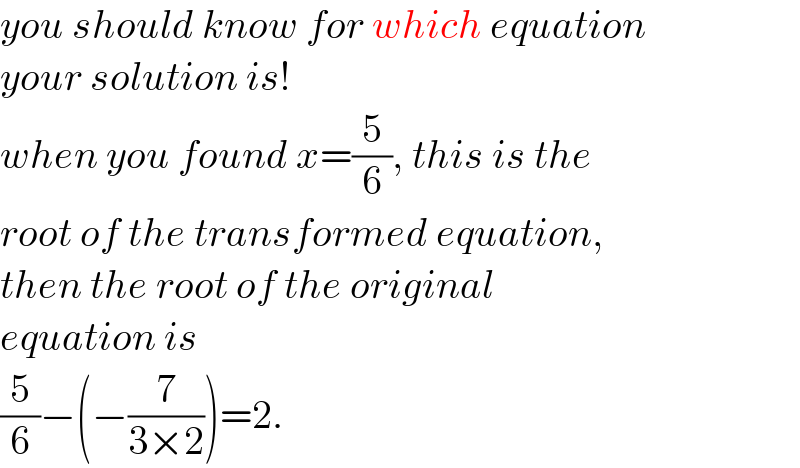
you should know for which equation your solution is! when you found x=(5/6), this is the root of the transformed equation, then the root of the original equation is (5/6)−(−(7/(3×2)))=2.

$${you}\:{should}\:{know}\:{for}\:{which}\:{equation} \\ $$$${your}\:{solution}\:{is}! \\ $$$${when}\:{you}\:{found}\:{x}=\frac{\mathrm{5}}{\mathrm{6}},\:{this}\:{is}\:{the} \\ $$$${root}\:{of}\:{the}\:{transformed}\:{equation},\: \\ $$$${then}\:{the}\:{root}\:{of}\:{the}\:{original}\: \\ $$$${equation}\:{is}\: \\ $$$$\frac{\mathrm{5}}{\mathrm{6}}−\left(−\frac{\mathrm{7}}{\mathrm{3}×\mathrm{2}}\right)=\mathrm{2}. \\ $$

Commented by Tawa11 last updated on 26/Feb/25

Ohh, thanks sir. It is not mention in the formula. Thanks sir.

$$\mathrm{Ohh},\:\mathrm{thanks}\:\mathrm{sir}.\:\mathrm{It}\:\mathrm{is}\:\mathrm{not}\:\mathrm{mention}\:\mathrm{in} \\ $$$$\mathrm{the}\:\mathrm{formula}. \\ $$$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$

Commented by Tawa11 last updated on 26/Feb/25

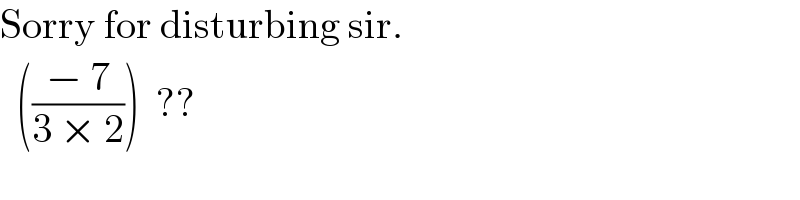
Sorry for disturbing sir. (((− 7)/(3 × 2))) ??

$$\mathrm{Sorry}\:\mathrm{for}\:\mathrm{disturbing}\:\mathrm{sir}. \\ $$$$\:\:\left(\frac{−\:\mathrm{7}}{\mathrm{3}\:×\:\mathrm{2}}\right)\:\:?? \\ $$

Commented by mr W last updated on 26/Feb/25

then you have not understood the formula or you applied the formula wrongly. show how you calculated!

$${then}\:{you}\:{have}\:{not}\:{understood}\:{the} \\ $$$${formula}\:{or}\:{you}\:{applied}\:{the}\:{formula} \\ $$$${wrongly}.\:{show}\:{how}\:{you}\:{calculated}! \\ $$

Commented by Tawa11 last updated on 26/Feb/25

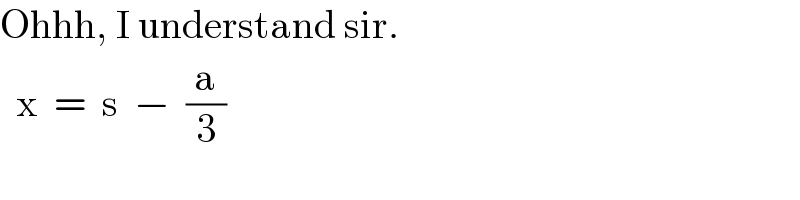
Ohhh, I understand sir. x = s − (a/3)

$$\mathrm{Ohhh},\:\mathrm{I}\:\mathrm{understand}\:\mathrm{sir}. \\ $$$$\:\:\mathrm{x}\:\:=\:\:\mathrm{s}\:\:−\:\:\frac{\mathrm{a}}{\mathrm{3}} \\ $$

Commented by Tawa11 last updated on 26/Feb/25

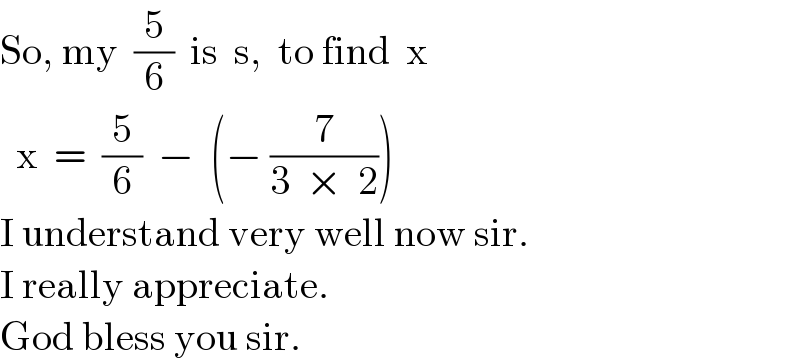
So, my (5/6) is s, to find x x = (5/6) − (− (7/(3 × 2))) I understand very well now sir. I really appreciate. God bless you sir.

$$\mathrm{So},\:\mathrm{my}\:\:\frac{\mathrm{5}}{\mathrm{6}}\:\:\mathrm{is}\:\:\mathrm{s},\:\:\mathrm{to}\:\mathrm{find}\:\:\mathrm{x} \\ $$$$\:\:\mathrm{x}\:\:=\:\:\frac{\mathrm{5}}{\mathrm{6}}\:\:−\:\:\left(−\:\frac{\mathrm{7}}{\mathrm{3}\:\:×\:\:\mathrm{2}}\right) \\ $$$$\mathrm{I}\:\mathrm{understand}\:\mathrm{very}\:\mathrm{well}\:\mathrm{now}\:\mathrm{sir}. \\ $$$$\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}. \\ $$$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com