Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 216799 by OPAVdx last updated on 20/Feb/25

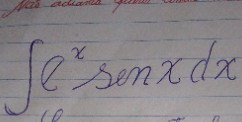
Commented by MathematicalUser2357 last updated on 22/Feb/25

sen?

$${sen}? \\ $$

Answered by MATHEMATICSAM last updated on 22/Feb/25

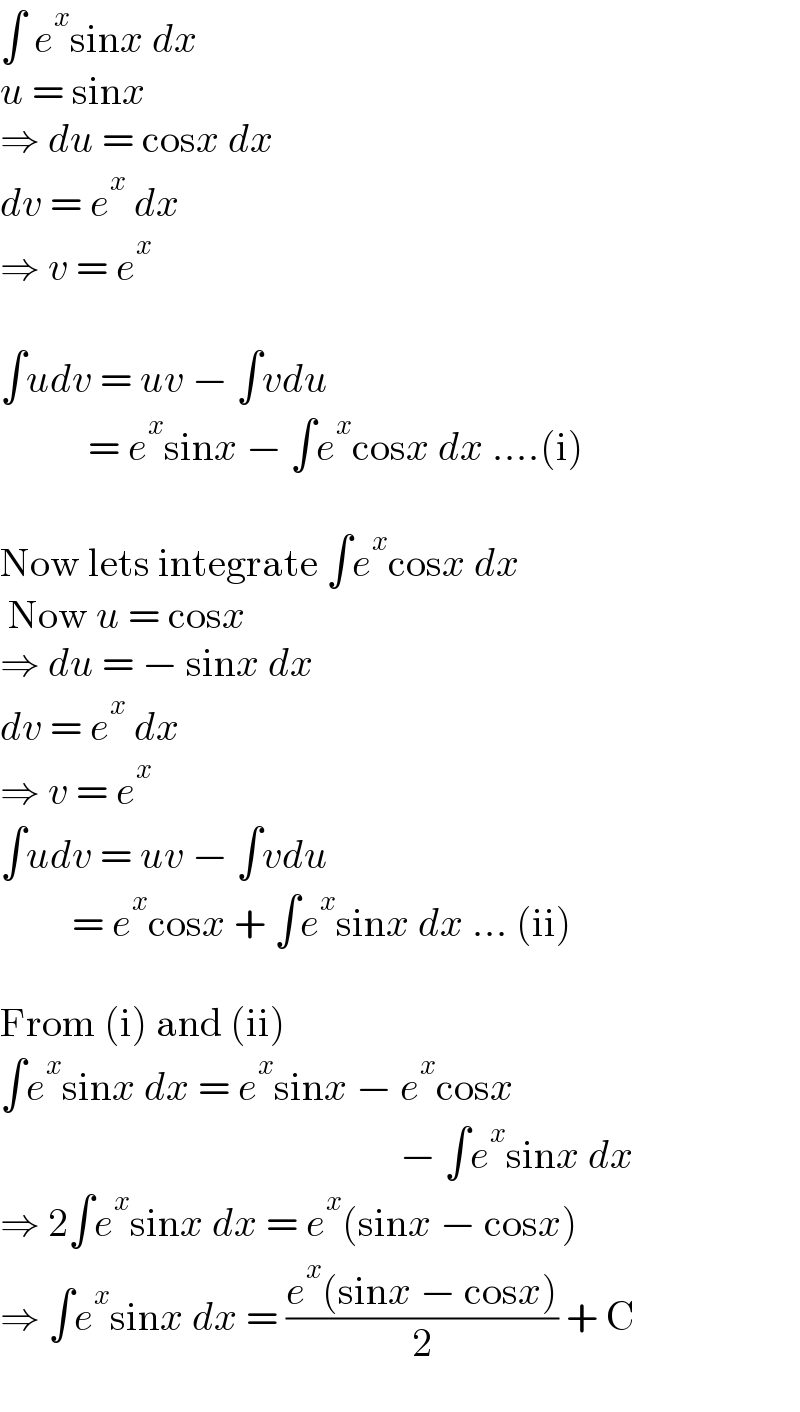
∫ e^x sinx dx u = sinx ⇒ du = cosx dx dv = e^x dx ⇒ v = e^x ∫udv = uv − ∫vdu = e^x sinx − ∫e^x cosx dx ....(i) Now lets integrate ∫e^x cosx dx Now u = cosx ⇒ du = − sinx dx dv = e^x dx ⇒ v = e^x ∫udv = uv − ∫vdu = e^x cosx + ∫e^x sinx dx ... (ii) From (i) and (ii) ∫e^x sinx dx = e^x sinx − e^x cosx − ∫e^x sinx dx ⇒ 2∫e^x sinx dx = e^x (sinx − cosx) ⇒ ∫e^x sinx dx = ((e^x (sinx − cosx))/2) + C

$$\int\:{e}^{{x}} \mathrm{sin}{x}\:{dx} \\ $$$${u}\:=\:\mathrm{sin}{x} \\ $$$$\Rightarrow\:{du}\:=\:\mathrm{cos}{x}\:{dx} \\ $$$${dv}\:=\:{e}^{{x}} \:{dx} \\ $$$$\Rightarrow\:{v}\:=\:{e}^{{x}} \\ $$$$ \\ $$$$\int{udv}\:=\:{uv}\:−\:\int{vdu} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:{e}^{{x}} \mathrm{sin}{x}\:−\:\int{e}^{{x}} \mathrm{cos}{x}\:{dx}\:....\left(\mathrm{i}\right) \\ $$$$ \\ $$$$\mathrm{Now}\:\mathrm{lets}\:\mathrm{integrate}\:\int{e}^{{x}} \mathrm{cos}{x}\:{dx} \\ $$$$\:\mathrm{Now}\:{u}\:=\:\mathrm{cos}{x} \\ $$$$\Rightarrow\:{du}\:=\:−\:\mathrm{sin}{x}\:{dx} \\ $$$${dv}\:=\:{e}^{{x}} \:{dx} \\ $$$$\Rightarrow\:{v}\:=\:{e}^{{x}} \\ $$$$\int{udv}\:=\:{uv}\:−\:\int{vdu} \\ $$$$\:\:\:\:\:\:\:\:\:=\:{e}^{{x}} \mathrm{cos}{x}\:+\:\int{e}^{{x}} \mathrm{sin}{x}\:{dx}\:...\:\left(\mathrm{ii}\right) \\ $$$$ \\ $$$$\mathrm{From}\:\left(\mathrm{i}\right)\:\mathrm{and}\:\left(\mathrm{ii}\right) \\ $$$$\int{e}^{{x}} \mathrm{sin}{x}\:{dx}\:=\:{e}^{{x}} \mathrm{sin}{x}\:−\:{e}^{{x}} \mathrm{cos}{x}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\:\int{e}^{{x}} \mathrm{sin}{x}\:{dx} \\ $$$$\Rightarrow\:\mathrm{2}\int{e}^{{x}} \mathrm{sin}{x}\:{dx}\:=\:{e}^{{x}} \left(\mathrm{sin}{x}\:−\:\mathrm{cos}{x}\right) \\ $$$$\Rightarrow\:\int{e}^{{x}} \mathrm{sin}{x}\:{dx}\:=\:\frac{{e}^{{x}} \left(\mathrm{sin}{x}\:−\:\mathrm{cos}{x}\right)}{\mathrm{2}}\:+\:\mathrm{C} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com