
Question Number 216703 by LMKhit last updated on 16/Feb/25
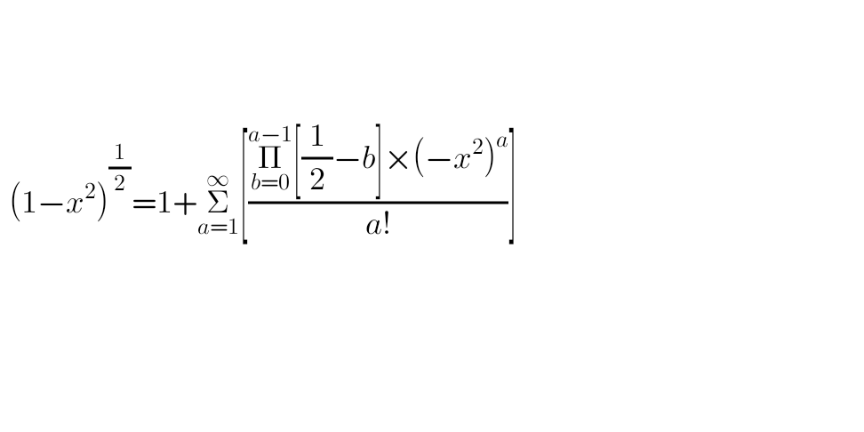
Answered by issac last updated on 16/Feb/25
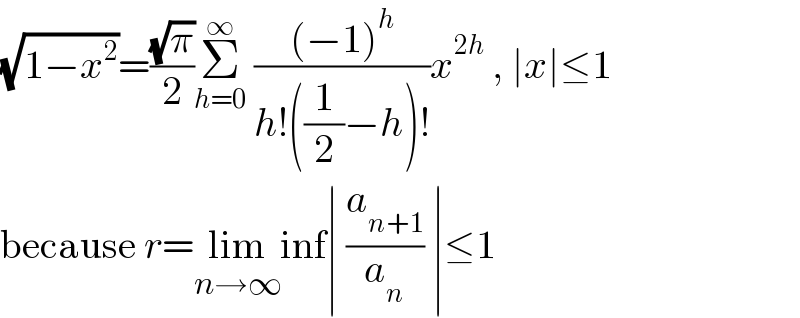
$$\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }=\frac{\sqrt{\pi}}{\mathrm{2}}\underset{{h}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\left(−\mathrm{1}\right)^{{h}} }{{h}!\left(\frac{\mathrm{1}}{\mathrm{2}}−{h}\right)!}{x}^{\mathrm{2}{h}} \:,\:\mid{x}\mid\leq\mathrm{1} \\ $$$$\mathrm{because}\:{r}=\underset{{n}\rightarrow\infty} {\mathrm{lim}inf}\mid\:\frac{{a}_{{n}+\mathrm{1}} }{{a}_{{n}} }\:\mid\leq\mathrm{1} \\ $$
